波函数模平方的分布和格林函数计算出的态密度分布,这两个是否是相同的?这个问题留了很久,但一直没做数值验证。因为按直觉来说,两者描述的是同一个物理图像。先放上结论:数值计算的结果验证了两者是一样的。
这里用方格子作为测试对象,算某个能级波函数模的平方分布以及格林函数计算出的态密度分布(经过了归一化)。Python代码如下:
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/962
"""
import numpy as np
def hamiltonian(width=2, length=4): # 有一定宽度和长度的方格子
h00 = np.zeros((width*length, width*length))
for i0 in range(length):
for j0 in range(width-1):
h00[i0*width+j0, i0*width+j0+1] = 1
h00[i0*width+j0+1, i0*width+j0] = 1
for i0 in range(length-1):
for j0 in range(width):
h00[i0*width+j0, (i0+1)*width+j0] = 1
h00[(i0+1)*width+j0, i0*width+j0] = 1
return h00
def main():
h0 = hamiltonian()
dim = h0.shape[0]
n = 4 # 选取第n个能级
eigenvalue, eigenvector = np.linalg.eig(h0) # 本征值、本征矢
# print(h0)
# print('哈密顿量的维度:', dim) # 哈密顿量的维度
# print('本征矢的维度:', eigenvector.shape) # 本征矢的维度
# print('能级(未排序):', eigenvalue) # 输出本征值。因为体系是受限的,所以是离散的能级
# print('选取第', n, '个能级,为', eigenvalue[n-1]) # 从1开始算,查看第n个能级是什么(这里本征值未排序)
# print('第', n, '个能级对应的波函数:', eigenvector[:, n-1]) # 查看第n个能级对应的波函数
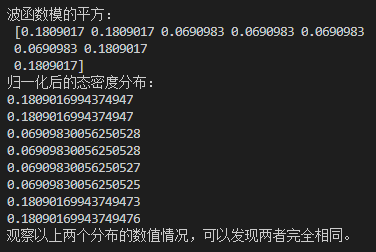
print('\n波函数模的平方:\n', np.square(np.abs(eigenvector[:, n-1]))) # 查看第n个能级对应的波函数模的平方
green = np.linalg.inv((eigenvalue[n-1]+1e-15j)*np.eye(dim)-h0) # 第n个能级对应的格林函数
total = np.trace(np.imag(green)) # 求该能级格林函数的迹,对应的是总态密度(忽略符号和系数)
print('归一化后的态密度分布:')
for i in range(dim):
print(np.imag(green)[i, i]/total) # 第n个能级单位化后的态密度分布
print('观察以上两个分布的数值情况,可以发现两者完全相同。')
if __name__ == '__main__':
main()
计算结果如下:
说明:
- 用波函数模平方计算的态密度分布,只能是严格位于能带的某个点上,即严格的k值和能量值。而用格林函数计算的态密度分布,通过调节虚数项在能量方向上可以有一定的展宽,同时k值可以偏离能带。
- 如果存在着简并,用格林函数求解的时候,是把几个波函数同时考虑进去了。求解波函数时用np.linalg.eigh可以得到相互正交的波函数。
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】
您好,请问这个计算态密度的方法可以用来计算一维模型吗?比如一维SSH模型。
都是可以的,有了哈密顿量,“波函数模方”和“基于格林方法的态密度”都可以计算。
那么是不是可以认为LDOS还是应该以归一化波函数的平方为准呀
LDOS也可以归一化,如果描述的是同一个物理,那么会和波函数的平方一致。
关老师,有个问题有点不理解哈。您在验证波函数模平方分布和格林函数计算的态密度分布时,对格林函数求解得到的结果也进行了归一化,我根据关老师您的代码也验证了一下,二者必须归一化才会相等。令我疑惑的是文献在利用格林函数计算LDOS时似乎并没有进行归一化处理,那么我们在计算LDOS时应该以哪一个为准呢?
用格林函数计算LDOS时,数值的数量级会受到能量虚部的影响,所以算出的绝对的数值没有意义。
波函数的模方得到的向量中的每个元素都分别对应实空间的某一个点吗?
嗯,这里的波函数是这样的,因为取的是紧束缚近似的基函数,且波函数具有对称性,所以波函数的中心是在格点上。
关老师您会计算局域态密度吗(LDOS),这似乎和态密度DOS不一样,它是实空间的
这里就是实空间的例子,不求和就是局域态密度LDOS。哈密顿量和波函数中的编号/索引和实空间位置有关系,是一一对应的。
好的谢谢您我研究下
老师您好,我最近在考虑边缘态的空间分布问题,所以对您这句话比较感兴趣:“哈密顿量和波函数中的编号/索引和实空间位置有关系,是一一对应的。”
我们计算能带时得到的是倒空间中的波函数,所以我想,当要求波函数在实空间的分布(或者说,粒子在实空间某一位置的概率密度)时应该对整个倒空间波函数用逆傅里叶变换得到实空间波函数,再求模的平方。
但是您所说的“一一对应”关系是说,倒空间中的坐标可以直接与实空间坐标一一对应吗?
我这里说的是实空间的哈密顿量。计算实空间的分布,用的是实空间的哈密顿量。
如果在x方向是无限长,可以考虑对动量kx积分,得到在y方向的总的分布。
谢谢您的解答!
我现在想要证明能带中出现的交叉是边缘态,所以想直接求出交叉两端对应波函数的分布。但是能给出来的只有倒空间的哈密顿矩阵,因为实空间的周期非常长。
目前想的也和您说的一样,对kx方向的/psi_{k_x}逆傅里叶变换再积分,应该可以得到/psi_y吧...
再次感谢,我再好好琢磨琢磨。
关老师您好,您这里的算法是只用了超前和延迟格林函数中的一个,但是这篇文章两个都用了(https://zhuanlan.zhihu.com/p/397762078),这其中的区别在哪呢?另外按照这篇文章的思路,计算局域态密度必须指定一个实空间的位置,也就是要涉及实空间波函数的分量,但是您的代码似乎并没有涉及波函数。
(1)公式是一样的,延迟格林函数和超前格林函数是厄密共轭的关系,两个相减得到的是虚部的两倍。(2)特征矢eigenvector就是本征波函数。
关老师,也就是np.imag(green)矩阵的对角元的某一部分就是指定的位置的LDOS吗?
是的,可以找些文献,有对应的公式。
谢谢关老师
关老师我想问一下,态密度公式中波函数的模方不是总是等于1吗?因为是同一个波函数,那为什么态密度公式还要加上波函数的模方呢?
或者更具体说,波函数的模方在数值计算里该怎么理解呢?
波函数的模方得到的向量的每个元素求和,是总等于1