准一维的方格子哈密顿量(以宽度3为例)为
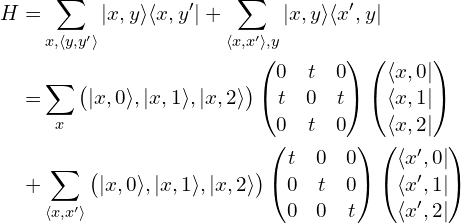
在上面最后的表达式中,第一项是H00,表示的是元胞内部的哈密顿量矩阵;第二项是H01,表示的是元胞间的跃迁矩阵。
1. 给出全部算法的代码
这里给出“用非平衡格林函数计算准一维方格子电导”的Python代码,相关公式见参考资料。其中用到戴森方程,格林函数![]() 公式参考这篇:使用Dyson方程迭代方法计算态密度(附Python代码)。
公式参考这篇:使用Dyson方程迭代方法计算态密度(附Python代码)。
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/948
"""
import numpy as np
import matplotlib.pyplot as plt
import copy
import time
def matrix_00(width=10): # 不赋值时默认为10
h00 = np.zeros((width, width))
for width0 in range(width-1):
h00[width0, width0+1] = 1
h00[width0+1, width0] = 1
return h00
def matrix_01(width=10): # 不赋值时默认为10
h01 = np.identity(width)
return h01
def main():
start_time = time.time()
h00 = matrix_00(width=5)
h01 = matrix_01(width=5)
fermi_energy_array = np.arange(-4, 4, .01)
plot_conductance_energy(fermi_energy_array, h00, h01)
end_time = time.time()
print('运行时间=', end_time-start_time)
def plot_conductance_energy(fermi_energy_array, h00, h01): # 画电导与费米能关系图
dim = fermi_energy_array.shape[0]
cond = np.zeros(dim)
i0 = 0
for fermi_energy0 in fermi_energy_array:
cond0 = np.real(conductance(fermi_energy0 + 1e-12j, h00, h01))
cond[i0] = cond0
i0 += 1
plt.plot(fermi_energy_array, cond, '-k')
plt.show()
def transfer_matrix(fermi_energy, h00, h01, dim): # 转移矩阵T。dim是传递矩阵h00和h01的维度
transfer = np.zeros((2*dim, 2*dim), dtype=complex)
transfer[0:dim, 0:dim] = np.dot(np.linalg.inv(h01), fermi_energy*np.identity(dim)-h00) # np.dot()等效于np.matmul()
transfer[0:dim, dim:2*dim] = np.dot(-1*np.linalg.inv(h01), h01.transpose().conj())
transfer[dim:2*dim, 0:dim] = np.identity(dim)
transfer[dim:2*dim, dim:2*dim] = 0 # a:b代表 a <= x < b,左闭右开
return transfer # 返回转移矩阵
def green_function_lead(fermi_energy, h00, h01, dim): # 电极的表面格林函数
transfer = transfer_matrix(fermi_energy, h00, h01, dim)
eigenvalue, eigenvector = np.linalg.eig(transfer)
ind = np.argsort(np.abs(eigenvalue))
temp = np.zeros((2*dim, 2*dim), dtype=complex)
i0 = 0
for ind0 in ind:
temp[:, i0] = eigenvector[:, ind0]
i0 += 1
s1 = temp[dim:2*dim, 0:dim]
s2 = temp[0:dim, 0:dim]
s3 = temp[dim:2*dim, dim:2*dim]
s4 = temp[0:dim, dim:2*dim]
right_lead_surface = np.linalg.inv(fermi_energy*np.identity(dim)-h00-np.dot(np.dot(h01, s2), np.linalg.inv(s1)))
left_lead_surface = np.linalg.inv(fermi_energy*np.identity(dim)-h00-np.dot(np.dot(h01.transpose().conj(), s3), np.linalg.inv(s4)))
return right_lead_surface, left_lead_surface # 返回右电极的表面格林函数和左电极的表面格林函数
def self_energy_lead(fermi_energy, h00, h01, dim): # 电极的自能
right_lead_surface, left_lead_surface = green_function_lead(fermi_energy, h00, h01, dim)
right_self_energy = np.dot(np.dot(h01, right_lead_surface), h01.transpose().conj())
left_self_energy = np.dot(np.dot(h01.transpose().conj(), left_lead_surface), h01)
return right_self_energy, left_self_energy # 返回右边电极自能和左边电极自能
def conductance(fermi_energy, h00, h01, nx=300): # 计算电导
dim = h00.shape[0]
right_self_energy, left_self_energy = self_energy_lead(fermi_energy, h00, h01, dim)
for ix in range(nx):
if ix == 0:
green_nn_n = np.linalg.inv(fermi_energy*np.identity(dim)-h00-left_self_energy)
green_0n_n = copy.deepcopy(green_nn_n) # 如果直接用等于,两个变量会指向相同的id,改变一个值,另外一个值可能会发生改变,容易出错,所以要用上这个COPY
elif ix != nx-1:
green_nn_n = np.linalg.inv(fermi_energy*np.identity(dim)-h00-np.dot(np.dot(h01.transpose().conj(), green_nn_n), h01))
green_0n_n = np.dot(np.dot(green_0n_n, h01), green_nn_n)
else:
green_nn_n = np.linalg.inv(fermi_energy*np.identity(dim)-h00-np.dot(np.dot(h01.transpose().conj(), green_nn_n), h01)-right_self_energy)
green_0n_n = np.dot(np.dot(green_0n_n, h01), green_nn_n)
gamma_right = (right_self_energy - right_self_energy.transpose().conj())*(0+1j)
gamma_left = (left_self_energy - left_self_energy.transpose().conj())*(0+1j)
transmission = np.trace(np.dot(np.dot(np.dot(gamma_left, green_0n_n), gamma_right), green_0n_n.transpose().conj()))
return transmission # 返回电导值
if __name__ == '__main__':
main()
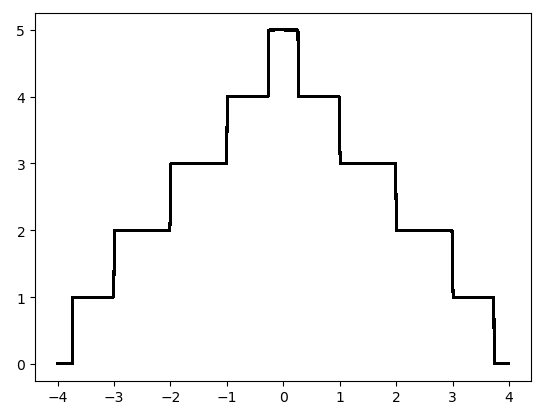
运行结果:
2. 使用Guan软件包
网址:https://py.guanjihuan.com/。
import guan
import numpy as np
fermi_energy_array = np.linspace(-4, 4, 400)
h00 = guan.hamiltonian_of_finite_size_system_along_one_direction(4)
h01 = np.identity(4)
conductance_array = guan.calculate_conductance_with_fermi_energy_array(fermi_energy_array, h00, h01)
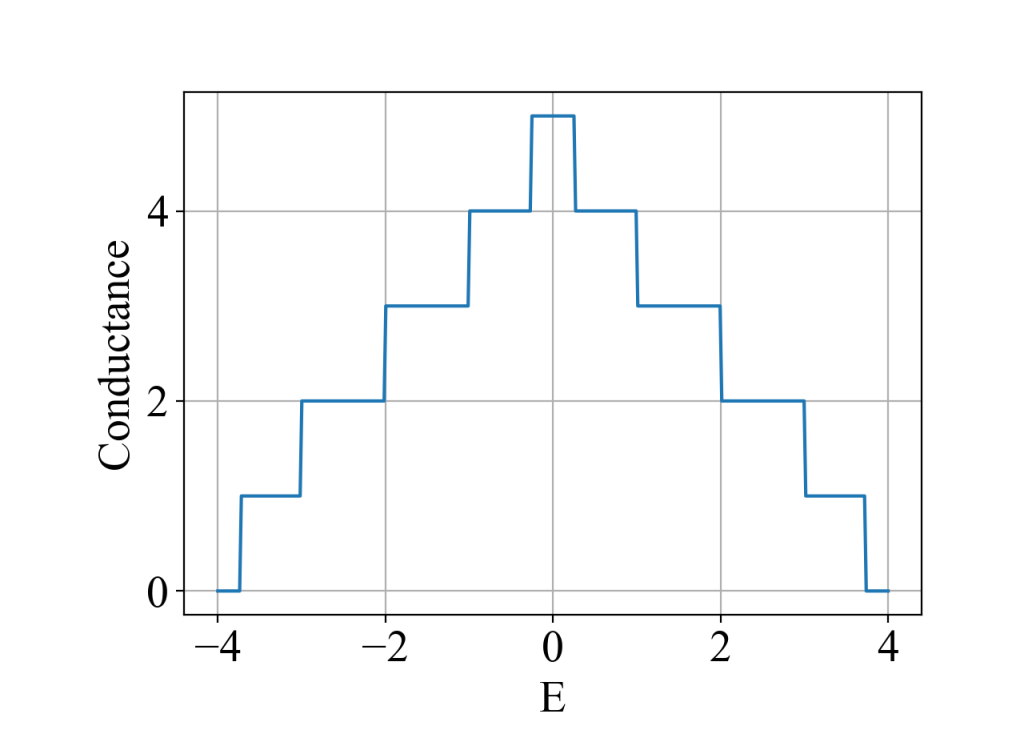
guan.plot(fermi_energy_array, conductance_array, xlabel='E', ylabel='Conductance', style='-')运行结果:
3. 使用Kwant软件包
访问这篇:https://www.guanjihuan.com/archives/2033。
参考文献:
[1] Landauer R. Electrical resistance of disordered one-dimensional lattices. The Philosophical Magazine: A Journal of Theoretical Experimental and Applied Physics, 1970, 21(172):863-867.
[2] Supriyo, Datta. Electronic transport in mesoscopic systems. 世界图书出版公司, 2004.
[5] Jintao Zhang, Electronic transport in Z-junction carbon nanotubes, J. Chem. Phys. 120, 7733 (2004).
[7] https://www.iue.tuwien.ac.at/phd/karamitaheri/node23.html
[8] https://sundoc.bibliothek.uni-halle.de/diss-online/07/07H039/t5.pdf
以上[8]链接可能已经失效,以下是对应的文件:
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】
博主您好!想问一下使用非平衡格点格林函数求解谱函数再根据公式得到态密度时,得到的密度矩阵可以直接使用对角部分对能量积分代表这一格点处的密度嘛?还是需要做一下对角化?
格林函数的对角元素就是和局域态密度有关,可以对能量积分的。我不知道你说的密度矩阵和对角化指的是什么。
请问博主,该代码在计算转移矩阵、表面格林函数、自能时用的h00和h01 应该针对的是电极的结构,这边是简单格子。然后在计算中心区递归格林函数迭代时,这里也是简单格子,所以在中心区迭代过程中的h00和h01与之前计算电极部分是一样的。我的问题是,如果中心区域不是简单格子,比如是石墨烯的zigzag边或者armchair边时,该中心区迭代过程代码中的h00和h01要根据所求的结构作相应的改变,请问这样想是否正确?
嗯,h00可以理解为条带的周期重复单元,即元胞。参考:石墨烯哈密顿量与能带图(附Python代码)。
博主,对于纯电子的输运,还有另外一种模型是电极取了本征态表象,这是每个电极都跟分子有作用;但我查了文献,对于这种情况自能的虚部可以取极限变成谱函数,自能的实部却没见人讨论过。想问博主做过这种模型吗
我没研究过这个
你好,请问计算左右表面格林函数自能时,电导应该等于uC'*GL*uC,为什么当uC取比您小的值时候,阶跃电导就不成形了
没看懂问题什么意思,什么是uC取值比较小的时候
请问为什么电导计算, 每个循环都有$自能和子能厄密共轭减 这一项呢
这个表达式定义的是Gamma矩阵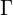 ,计算电导的公式包含这个。公式:
,计算电导的公式包含这个。公式: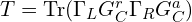 。原来程序中我直接用self_energy的名字来赋值了,覆盖原来的值,目前程序已改成gamma_left和gamma_right,会更直观点。
。原来程序中我直接用self_energy的名字来赋值了,覆盖原来的值,目前程序已改成gamma_left和gamma_right,会更直观点。
博主你好,我看的输运的文献一般考虑的都是线性偏压,请问线性偏压和非线性偏压的区别是什么?
线性偏压应该就是指小电压,电导为固定值。如果偏压比较大时,电压差对实际电导会有影响,也就是非线性的,需要由新的理论和公式来描述。
那此时非平衡格林函数方法是不是不再适用了?
算是吧。可以参考这本书:Datta - 2005 - Quantum Transport Atom to Transistor。
以下摘抄自这本书的序言:
ETMS (Electronic Transport in Mesoscopic Systems, Datta, 1995) was largely about low-bias conductance (“linear response”) and its physical interpretation for small conductors, emphasizing the transmission formalism. In this book (Chapters 1, 8–11) I have stressed the full current–voltage characteristics and the importance of performing self-consistent calculations. I have tried to inject appropriate insights from the transmission formalism, like the Landauer formula and Buttiker probes, but the emphasis is on the non-equilibrium Green’s function (NEGF) formalism which I believe provides a rigorous framework for the development of quantum device models that can be used to benchmark other simplified approaches. It bridges the gap between the fully coherent quantum transport models of mesoscopic physicists and the fully incoherent Boltzmann transport models of device physicists.
另外,Datta的这本书《Electronic Transport In Mesoscopic Systems》第42页有提到:For linear response we conceptually let the bias tend to zero; that is,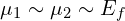 .
.
如果考虑有一定的偏压,类似于这篇文章Quantized four-terminal resistances in a ferromagnetic graphene p–n junction,用到的仍然是非平衡格林函数,但这个我不确定是否归于非线性的情况。
博主,请问你用过kubo formula计算过电导么?它与非平衡格林函数方法有什么区别?它是纯解析的么?也能程序化么?
我还没用kubo formula算过。只要有公式都能用程序来表示。
两种方法应该是等价的,以下摘抄自参考资料Quantum Transport in Finite Disordered Electron Systems的第48页:
It was proven rigorously [71, 93] that Landauer formula can be derived from the Kubo formula. This requires to use the Kubo NLCT for a finite-size system connected to ideal leads (which stem from the “sample-specific linear response theory” [89]). The proof goes through the integration of NLCT over the surfaces, as in Eq. (2.19). The surfaces should be positioned deep inside the leads so that all evanescent modes have “died out” and do not contribute to the conductance. The equivalence shows that transmission properties can be calculated from the Kubo NLCT (2.46). It also confirms the independence of linear transport properties on the local current and field distribution (cf. Sec. 2.2), i.e., non-equilibrium charge redistribution, since no such quantities enter into the Landauer formula for conductance.
请问博主有详细介绍kubo formula的资料和书籍么?尤其是体系存在disorder情况下的kubo formula。
分享的这个链接“Quantum Transport in Finite Disordered Electron Systems”里好像就有介绍,还里有这篇的参考文献。其他的你可以网上搜下,目前我这边也没有什么资料。
right_lead_surface = np.linalg.inv(fermi_energy*np.identity(dim)-h00-np.dot(np.dot(h01, s2), np.linalg.inv(s1))) 请问这里计算表面格林函数的方法有参考的文章吗?我想了解一下。我导师给我的文章计算SGF的方法和这个不一样。 Quick iterative scheme for the calculation of transfer matrices: application to Mo (100) 这是我参考的SGF的方法。
在参考文献中找到了
博主,您这个最开始写的哈密顿量是在实空间中,讲道理如果一个方向周期边条另一个方向开边条,倒空间哈密顿量应该含k,程序里您是使用的实空间哈密顿量?不需要傅里叶变换么?
量子输运的程序一般是用到实空间的哈密顿量,如元胞H00和跃迁项H01。考虑的体系在量子输运的方向上的确是无限长的。在算法中是把两个半无限的电极以自能的形式并入中心体系,最终得到总的格林函数。
So nice!