狄拉克矩阵 Dirac Matrix

这是之前的一篇：泡利矩阵以及泡利矩阵的张量积。

狄拉克矩阵（Dirac Matrix）又叫Gamma矩阵 $\{\gamma_0, \gamma_1, \gamma_2, \gamma_3\}$ ，是在狄拉克方程中推导出来的 $4\times 4$ 的矩阵，满足Clifford代数。狄拉克矩阵可以写成泡利矩阵的张量积形式[1-4]：

$\gamma_0=\tau_3 \otimes\sigma_0$

$\gamma_k=i \tau_2 \otimes\sigma_k \quad (k=1, 2, 3)$

第五个Gamma矩阵可以定义为：

$\gamma_5=i \gamma_0 \gamma_1 \gamma_2 \gamma_3 = \tau_1 \otimes\sigma_0$

具体写为：

$\gamma_0=\tau_3 \otimes\sigma_0=\begin{pmatrix}\sigma_0 & 0 \\0 & -\sigma_0\end{pmatrix}=\begin{pmatrix}1 & 0 & & \\0 & 1 & & \\& & -1 & 0 \\& & 0 & -1\end{pmatrix}$

$\gamma_1=i\tau_2 \otimes\sigma_1=\begin{pmatrix}0 & \sigma_x \\-\sigma_x & 0\end{pmatrix}=\begin{pmatrix}& & 0 & 1 \\& & 1 & 0 \\0 & -1 & & \\-1 & 0 & &\end{pmatrix}$

$\gamma_2=i\tau_2 \otimes\sigma_2=\begin{pmatrix}0 & \sigma_y \\-\sigma_y & 0\end{pmatrix}=\begin{pmatrix}& & 0 & -i \\& & i & 0 \\0 & i & & \\-i & 0 & &\end{pmatrix}$

$\gamma_3=i\tau_2 \otimes\sigma_3=\begin{pmatrix}0 & \sigma_z \\-\sigma_z & 0\end{pmatrix}=\begin{pmatrix}& & 1 & 0 \\& & 0 & -1 \\-1 & 0 & & \\0 & 1 & &\end{pmatrix}$

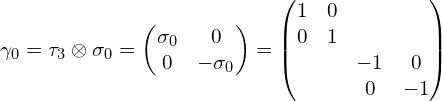
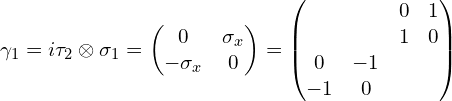
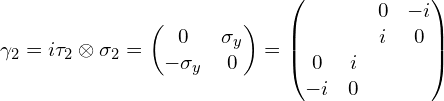
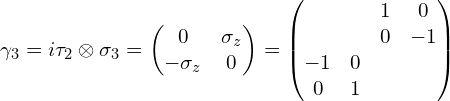
第五个Gamma矩阵：

$\gamma_5=i \gamma_0 \gamma_1 \gamma_2 \gamma_3 = \tau_1 \otimes\sigma_0=\begin{pmatrix}0 & \sigma_0 \\\sigma_0 & 0\end{pmatrix}=\begin{pmatrix}& & 1 & 0 \\& & 0 & 1 \\1 & 0 & & \\0 & 1 & &\end{pmatrix}$

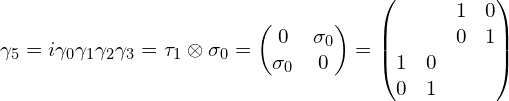
以上的矩阵是在Dirac表象下的形式。此外还有在Weyl (chiral) 表象、Weyl (chiral) (alternate form)表象、 Majorana表象下的形式[1,2]。总结为：

1. Dirac表象

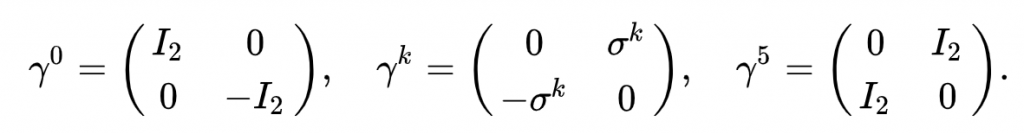
2. Weyl (chiral)表象

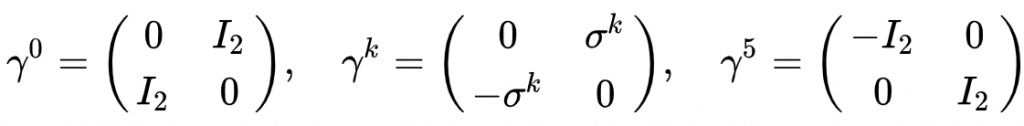
3. Weyl (chiral) (alternate form)表象

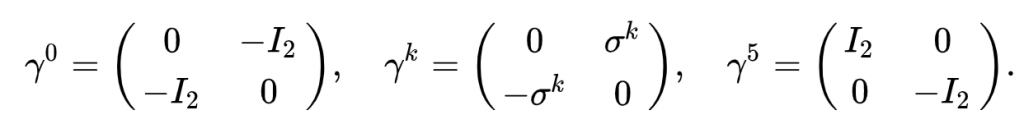
4. Majorana表象

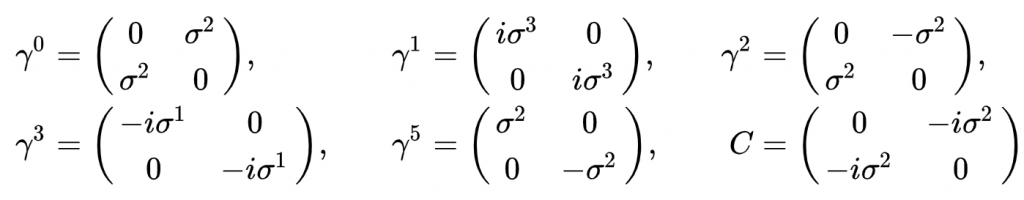
其中，C表示的是charge conjugation matrix。

参考资料：

[1] https://en.wikipedia.org/wiki/Gamma_matrices

[2] https://www.mathphysicsbook.com/mathematics/clifford-groups/classification-of-clifford-algebras/pauli-and-dirac-matrices/

[3] https://encyclopediaofmath.org/wiki/Dirac_matrices

[4] https://www.physi.uni-heidelberg.de/~uwer/lectures/StandardModel2010/Exercises/exercise-3.pdf

6,580 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】

4 thoughts on “狄拉克矩阵 Dirac Matrix”

原始Dirac方程是用4*4矩阵表达的，但到氢原子的时候，Dirac代数将它化成了2*2矩阵，目的是得到氢原子的精细能级结构公式。从逻辑上讲，4*4矩阵对应的Dirac方程是一个4元一阶微分方程组，2*2矩阵对应的Dirac方程是一个2元一阶微分方程组。一个4元一阶微分方程组因为一种个人的代数理论化成了一个2元一阶微分方程组，你如何理解这一数学技术？

guanjihuan说道：

2022年4月27日 18:57

有可能是因为两个2*2矩阵是相互解耦合的（decoupled）吧，不可约表示的维度就是2。或者可能做了某种近似。具体情况我不了解。

回复
1. 匿名说道：
  
  2022年4月30日 22:40
  
  谢谢你的真诚。我在读Dirac理论时，发现似乎没有理论物理学家真正搞懂过Dirac四矩阵问题，而后来的理论物理学家只不过抄袭Dirac。但Dirac那帮人非常狡猾，中间搞了一个非常复杂的Dirac代数（可参阅曾谨言的量子力学卷II）把四矩阵对应的四分量波函数微分方程组，绕了几个轮回使大家都被绕糊涂的时候，变魔术一般化成了二矩阵对应的二分量波函数，目的就是要拼凑出所谓精细结构能够能公式。查资料查到你这儿来了。这年头能花时间和精力搞这些东西的人，全世界已经曲指可数了。祝你不断取得突破。
  
  回复
  1. guanjihuan说道：
    
    2022年5月1日 05:16
    
    嗯，感谢你的肯定。我对你说的这个没做过深入的研究，不是很了解，有可能是做了近似，投影降维了。
    
    回复