在用格林函数算态密度时,费米能E需要加一个无穷小的虚数项eta,即E'=E+i*eta。这个虚数项eta应该取多大呢?本篇主要讨论这个问题。
先列出结论:
- eta的取值不能太小。eta太小时由于计算精度不高,往往不能很好地显示出态密度分布。如果eta的取值比较小,态密度的计算精度也要相应地提高。此外,eta取一定的值在某种程度上可以掩盖住没必要的小带隙使得态密度连续,更容易体现出体的性质,忽略尺寸效应的影响。
- eta的取值不能太大。eta太大时由于能带的展宽,多个带之间的态密度分布相互接触,使得在能量方向上连续(即无带隙),这并不能反应出真实的能带情况。
- eta的取值至少要比能带中最小带隙还小一个数量级,才能反应出真实的能带情况。
下面是具体的讨论。
Part I:
在这篇博文“数值验证“波函数模平方分布”和“格林函数计算的态密度分布”的关系(附Python代码)”中,虚数项取的相对比较小,为 eta=1e-15。结果为:
波函数模的平方:
[0.1809017 0.1809017 0.0690983 0.0690983 0.0690983 0.0690983 0.1809017
0.1809017]
归一化后的态密度分布:
0.18090169943749468
0.18090169943749468
0.06909830056250525
0.06909830056250525
0.06909830056250528
0.06909830056250525
0.18090169943749473
0.18090169943749476如果 eta=1e-2,结果为:
波函数模的平方:
[0.1809017 0.1809017 0.0690983 0.0690983 0.0690983 0.0690983 0.1809017
0.1809017]
归一化后的态密度分布:
0.18087649012161847
0.1808764901216186
0.06912350987838145
0.0691235098783815
0.06912350987838146
0.06912350987838142
0.1808764901216186
0.18087649012161852可以看出:当eta取比较大时,虽然由格林函数计算得到的归一化态密度和波函数模的平方相比有一点偏移,但差别也不是太明显。因为费米能是固定在某一个值(在某个能级)上,所以并不能看到态密度的展宽情况。
Part II:
在这篇博文“方格子和石墨烯的态密度与费米能的关系(附Python代码)”中,eta 的取值相对较大,eta 取为 0.1,结果为:
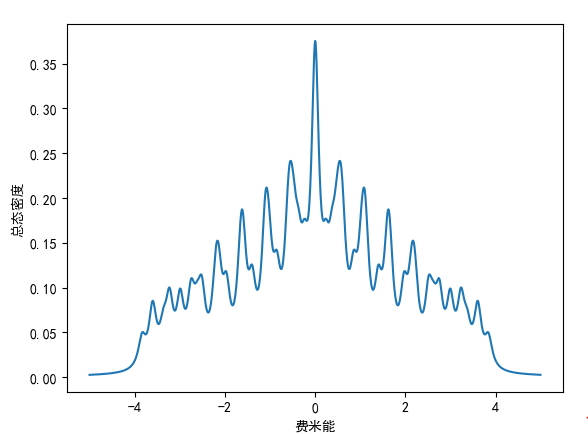
当 eta=0.05 时,结果为:
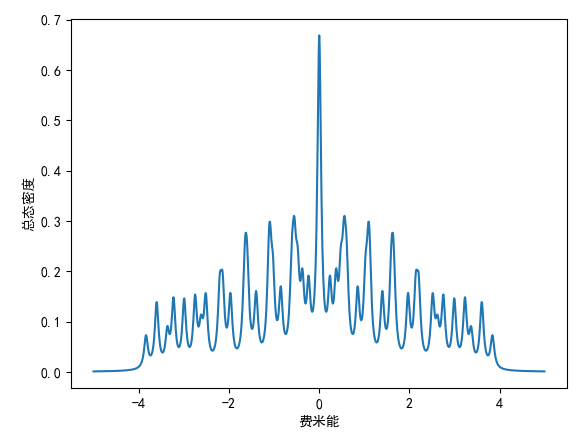
当 eta=0.01 时,结果为:
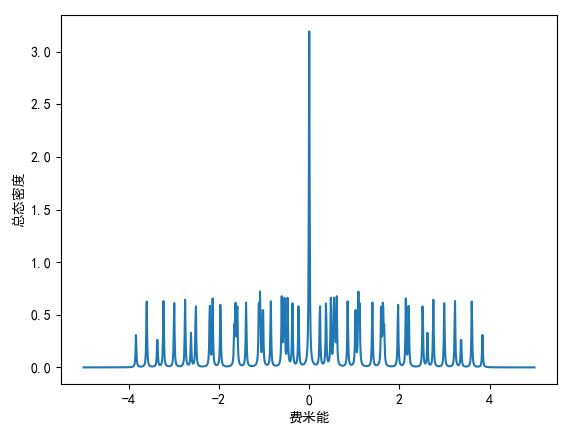
当 eta=0.001 时,结果为:
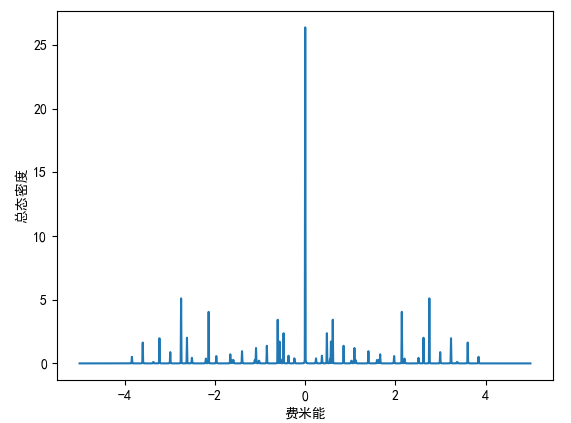
eta=0.001 的结果显然有点问题,这是由于在代码中计算精度不高(在代码中 plot_precision = 0.01)。
调高精度 plot_precision = 0.0001,同时 eta=0.001,计算结果为:
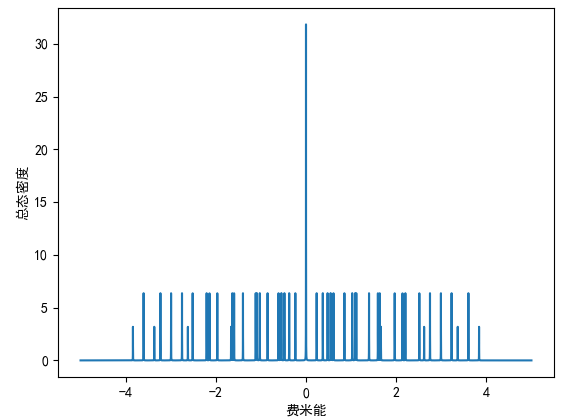
直接对方格子实空间的哈密顿量求本征值,得到 100 个离散的值:
[-3.83797189e+00 -3.60149301e+00 -3.60149301e+00 -3.36501413e+00
-3.22870742e+00 -3.22870742e+00 -2.99222853e+00 -2.99222853e+00
-2.74981597e+00 -2.74981597e+00 -2.61944294e+00 -2.51333709e+00
-2.51333709e+00 -2.20361562e+00 -2.20361562e+00 -2.14055149e+00
-2.14055149e+00 -1.96713674e+00 -1.96713674e+00 -1.66166005e+00
-1.63435627e+00 -1.63435627e+00 -1.59435114e+00 -1.59435114e+00
-1.39787739e+00 -1.39787739e+00 -1.11545970e+00 -1.11545970e+00
-1.08815592e+00 -1.08815592e+00 -1.02509179e+00 -1.02509179e+00
-8.51677040e-01 -8.51677040e-01 -6.09264479e-01 -6.09264479e-01
-5.69259353e-01 -5.46200349e-01 -5.46200349e-01 -4.78891442e-01
-4.78891442e-01 -3.72785598e-01 -3.72785598e-01 -2.36478882e-01
-2.36478882e-01 -2.63817921e-15 -3.06761504e-16 -1.67151171e-16
-9.33807309e-17 2.97584518e-17 8.90378852e-17 1.98974164e-16
2.53683193e-16 6.17862440e-16 2.11252069e-15 2.36478882e-01
2.36478882e-01 3.72785598e-01 3.72785598e-01 4.78891442e-01
4.78891442e-01 5.46200349e-01 5.46200349e-01 5.69259353e-01
6.09264479e-01 6.09264479e-01 8.51677040e-01 8.51677040e-01
1.02509179e+00 1.02509179e+00 1.08815592e+00 1.08815592e+00
1.11545970e+00 1.11545970e+00 1.39787739e+00 1.39787739e+00
1.59435114e+00 1.59435114e+00 1.63435627e+00 1.63435627e+00
1.66166005e+00 1.96713674e+00 1.96713674e+00 2.14055149e+00
2.14055149e+00 2.20361562e+00 2.20361562e+00 2.51333709e+00
2.51333709e+00 2.61944294e+00 2.74981597e+00 2.74981597e+00
2.99222853e+00 2.99222853e+00 3.22870742e+00 3.22870742e+00
3.36501413e+00 3.60149301e+00 3.60149301e+00 3.83797189e+00]通过以上的例子,可以得到第一个结论:eta 的取值不能太小。eta 太小时由于计算精度不高,往往不能很好地显示出态密度分布。如果 eta 的取值比较小,态密度的计算精度也要相应地提高。此外,eta 取一定的值在某种程度上可以掩盖住没必要的小带隙使得态密度连续,更容易体现出体的性质,忽略尺寸效应的影响。
Part III:
在上面的例子中方格子的长宽都是 10。为了更方便的说明问题,在接下来的计算中方格子的长宽都设为 5。计算精度 plot_precision = 0.0001。
当 eta=0.001 时,结果为:
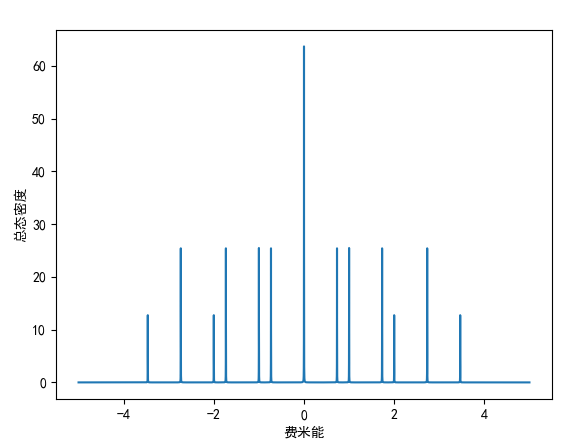
当 eta=0.01时,结果为:
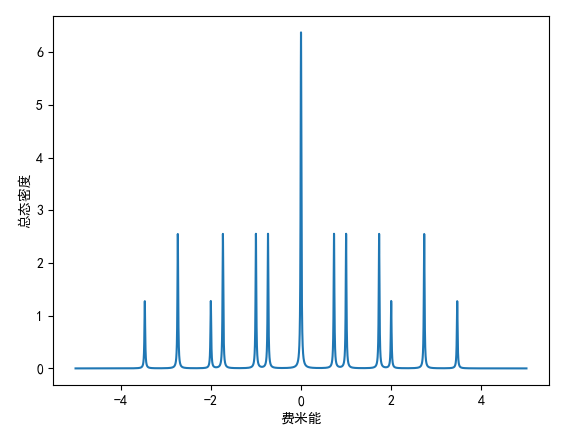
当 eta=0.1时,结果为:
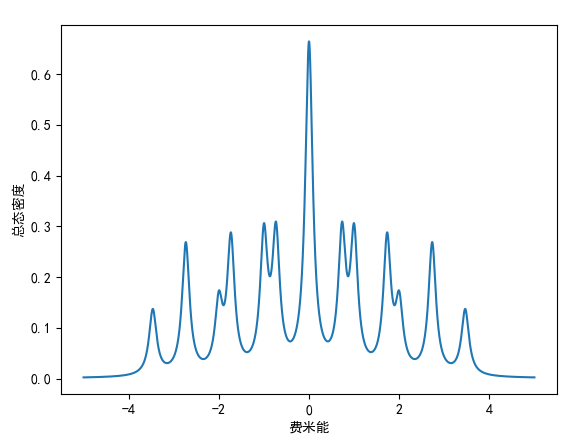
直接对方格子实空间的哈密顿量求本征值,得到25个离散的值:
[-3.46410162e+00 -2.73205081e+00 -2.73205081e+00 -2.00000000e+00
-1.73205081e+00 -1.73205081e+00 -1.00000000e+00 -1.00000000e+00
-7.32050808e-01 -7.32050808e-01 -2.72232680e-15 -1.57988160e-15
-5.32704115e-16 -4.96367655e-16 1.39812852e-16 7.32050808e-01
7.32050808e-01 1.00000000e+00 1.00000000e+00 1.73205081e+00
1.73205081e+00 2.00000000e+00 2.73205081e+00 2.73205081e+00
3.46410162e+00]通过以上的例子,可以得到第二个结论:eta 的取值不能太大。eta 太大时由于能带的展宽,多个带之间的态密度分布相互接触,使得在能量方向上连续(无带隙),这并不能反应出真实的能带情况。
Part IV:
在接下来的计算中方格子的长宽都设为 2。计算精度 plot_precision = 0.0001。
对方格子求本征值,得到 4 个离散的值:
[-2.00000000e+00 -1.11310287e-16 3.33354892e-16 2.00000000e+00]当 eta=0.01 时,结果为:
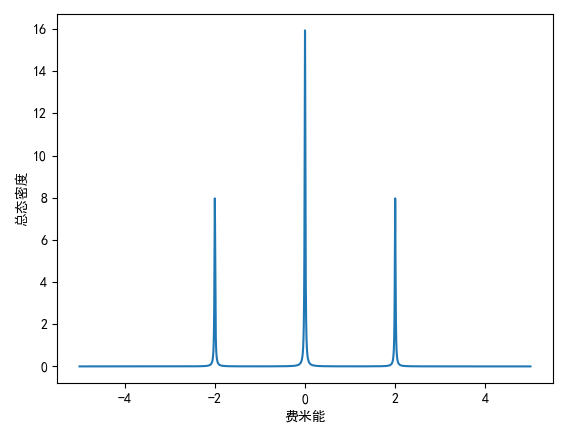
当 eta=0.1 时,结果为:
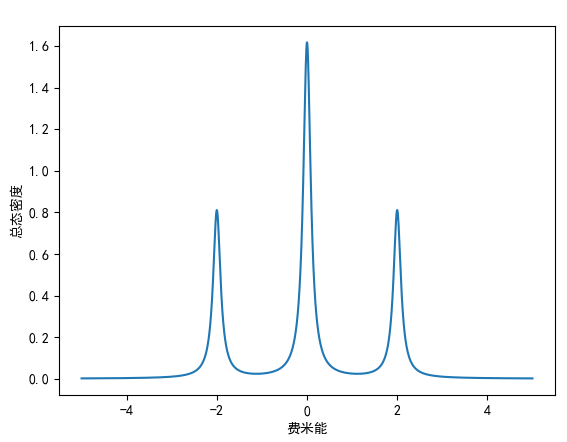
当 eta=0.2 时,结果为:
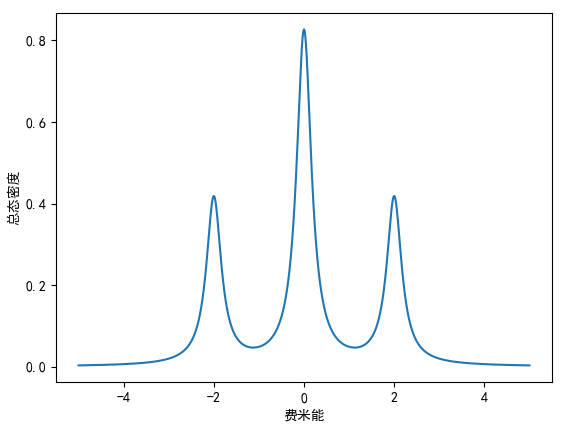
当 eta=0.5 时,结果为:
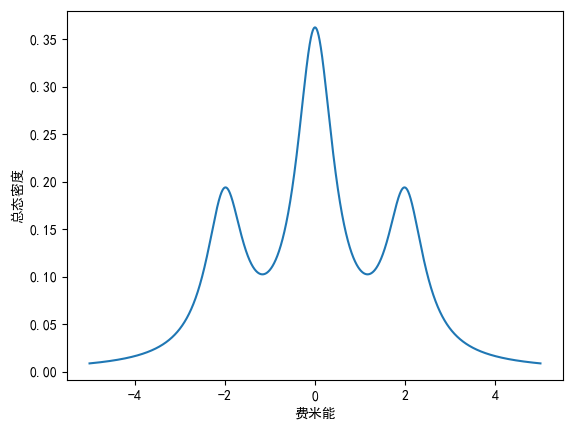
当 eta=1.0 时,结果为:
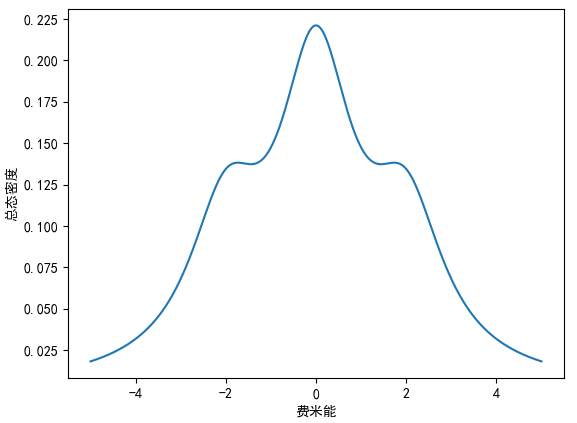
通过以上观察,可以得到第三个结论:eta的取值至少要比能带中最小带隙还小一个数量级,才能反应出真实的能带情况。
本篇只是经验上的分析。在参考资料[1]中有更详细的讨论,同时也讲出了虚数项的的物理意义。这里截图出第211页的一部分内容:

参考资料:
[1] Quantum Transport: Atom to Transistor (Supriyo Datta) 中第11页开始、第191页开始、第207页开始。
[2] Calculating Green functions from finite systems
[3] https://www.iue.tuwien.ac.at/phd/karamitaheri/node23.html
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】
关博您好,有限深势阱如何利用格林函数求解态密度呢
你可以试着根据格林函数的定义,给出有限深势阱的格林函数的解析表达式,然后态密度就在对角的虚部上。在数值上,你可以先把有限深势阱离散化,得到离散的有限深势阱哈密顿量,然后求逆矩阵得到格林函数,进而得到态密度。具体你可以找些资料参考下,或者问问ChatGPT。
太感谢您啦
关老师您好,根据您的指导已经有了初步结果,十分感谢您。目前的疑问是,如果对一维有限深势阱进行哈密顿量离散化,然后得到格林函数,再得到的态密度是否是一个维度方向上的态密度,如您这篇文章的结果。如果我想得到与传统相似的二维台阶形式的态密度,是否需要对有限深势阱进行三维哈密顿量离散化,或者说其他处理,求教。
一维有限深势阱离散化后还是一个维度方向上的。我不清楚你后面说的是什么意思,如果考虑的是二维势阱,那么同样对其离散化即可。
博主你好,十分感谢你的记录。
我有些问题,
1)这里你引用的Datta书中的 "it is important to choose a value of the “infinitesimal” 0+ that is in excess of ε in order to turn them into well-behaved reservoirs.",这里不应该是说 我们选取的eta值要大于 \delta E 吗?
2) finite-level spacing \delta E 指的是我们选择的能量间隔dE吗? 对于输运计算而言,我们需要事先给出 eta值。我查阅了 WannierTools 的部分代码(计算Green函数), 有些地方的eta值是根据能量的网格来确定的.
3) 从您文章也能看出, 不同的eta对应的态密度不一样,态密度强度也不一样,这态密度峰值大小有物理意义吗?
感谢!
(1)这里指的是电极,需要类似于金属的性质,即well-behaved reservoirs,所以选取的eta值要大于 \delta E。好像不是指我们需要关心的中心体系。
(2)能量间隔和能量网格应该是同一回事。
(3)这里计算出来的峰值好像没有太大意义,可以对态密度分布进行归一化处理。
感谢关博的回答!