方格子的霍夫斯塔特蝴蝶（附Python代码）

霍夫斯塔特蝴蝶（Hofstadter butterfly）的文献：Douglas R. Hofstadter, "Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields", Phys. Rev. B 14, 2239 (1976).

有限体系方格子的哈密顿量：方格子模型在实空间中的哈密顿量形式。

引入磁场：佩尔斯替换 Peierls substitution。

霍夫斯塔特蝴蝶的代码为：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/8491
"""

import numpy as np
import cmath
import matplotlib.pyplot as plt


def main():
    for n in np.arange(1, 11):
        print('n=', n)
        width = n
        length = n
        B_array = np.arange(0, 1, 0.001)
        eigenvalue_all = np.zeros((B_array.shape[0], width*length))
        i0 = 0
        for B in B_array:
            # print(B)
            h = hamiltonian(width, length, B)
            eigenvalue, eigenvector = np.linalg.eig(h)
            eigenvalue_all[i0, :] = np.real(eigenvalue)
            i0 += 1
        plt.plot(B_array, eigenvalue_all, '.r', markersize=0.5)
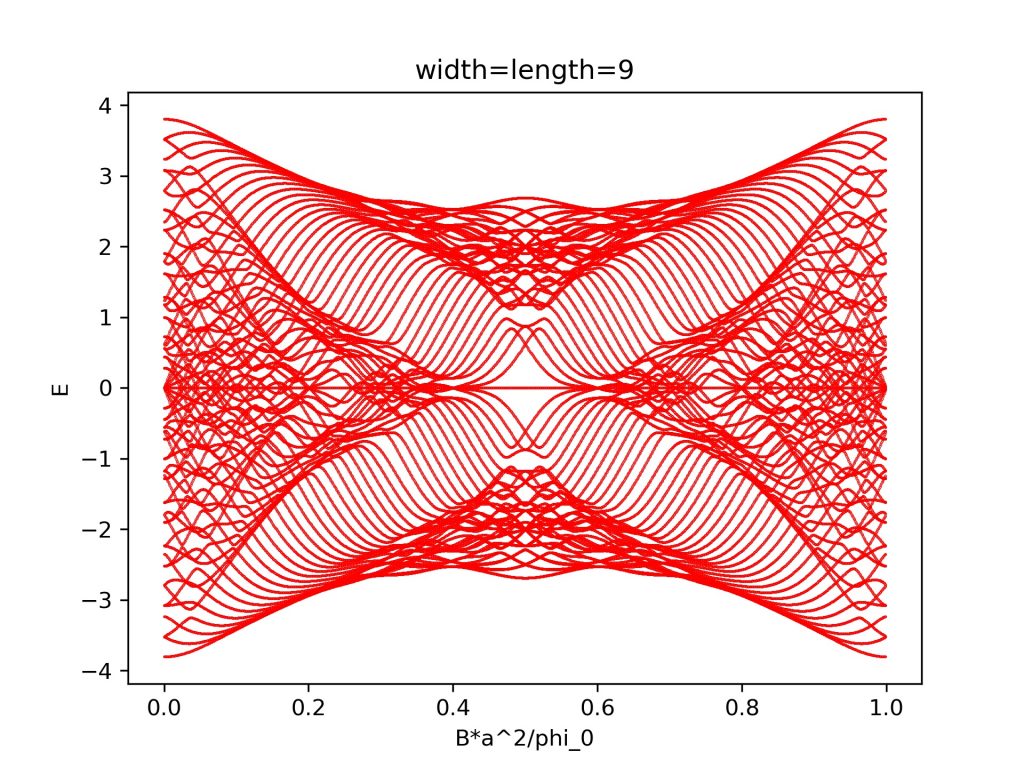
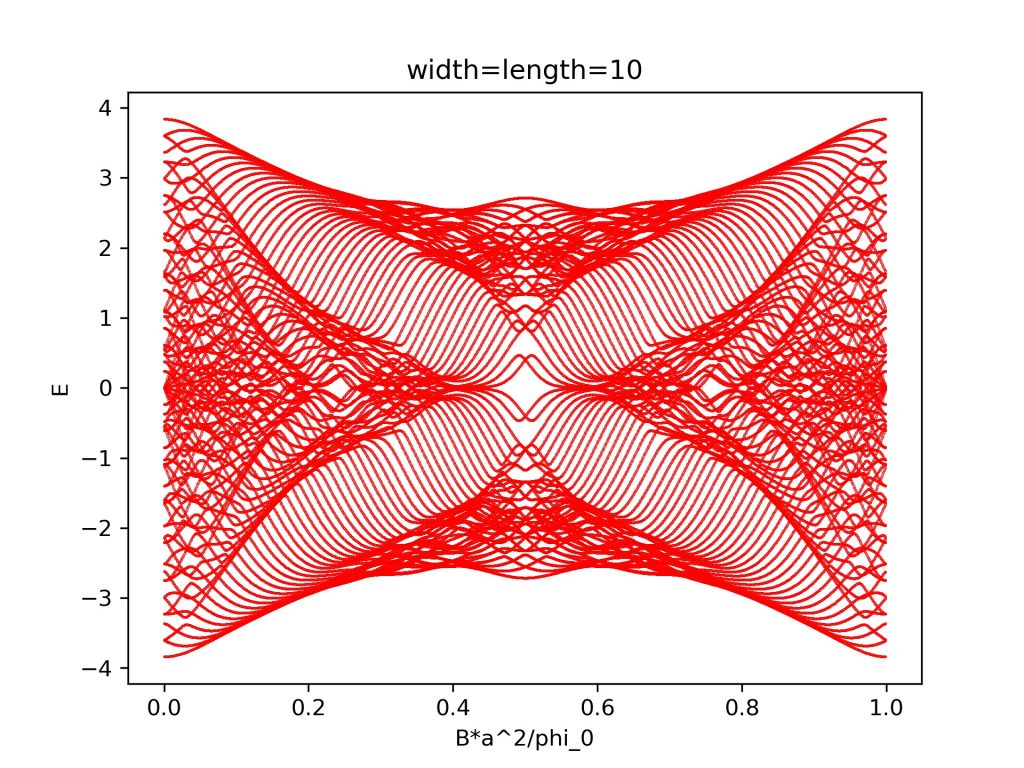
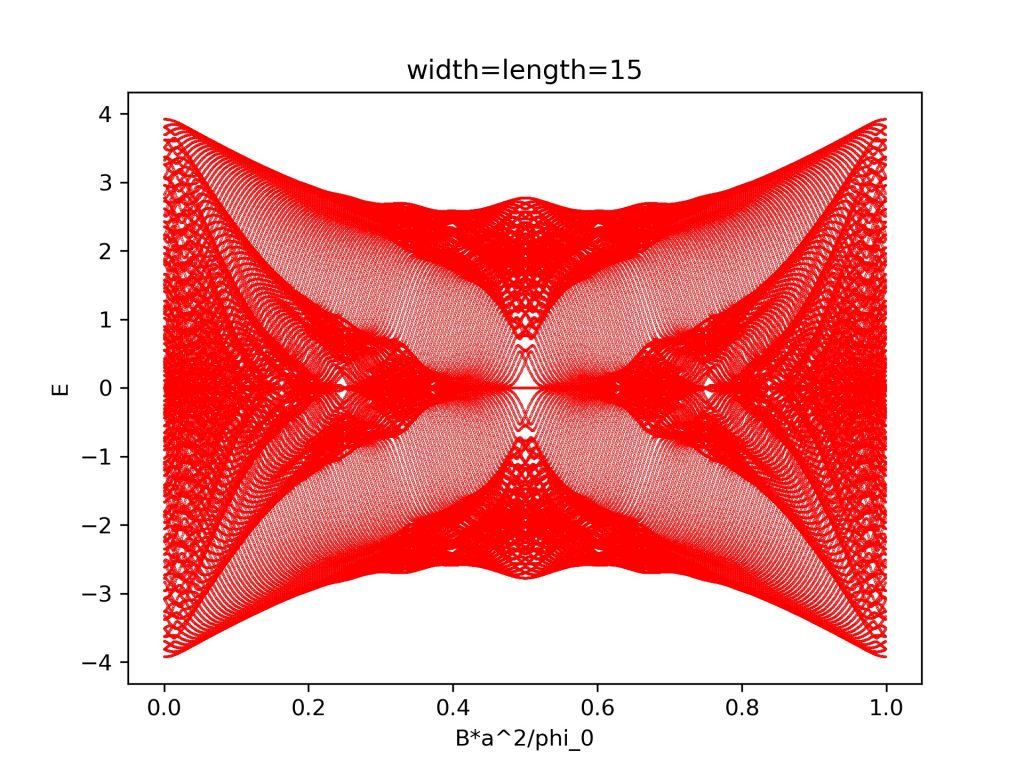
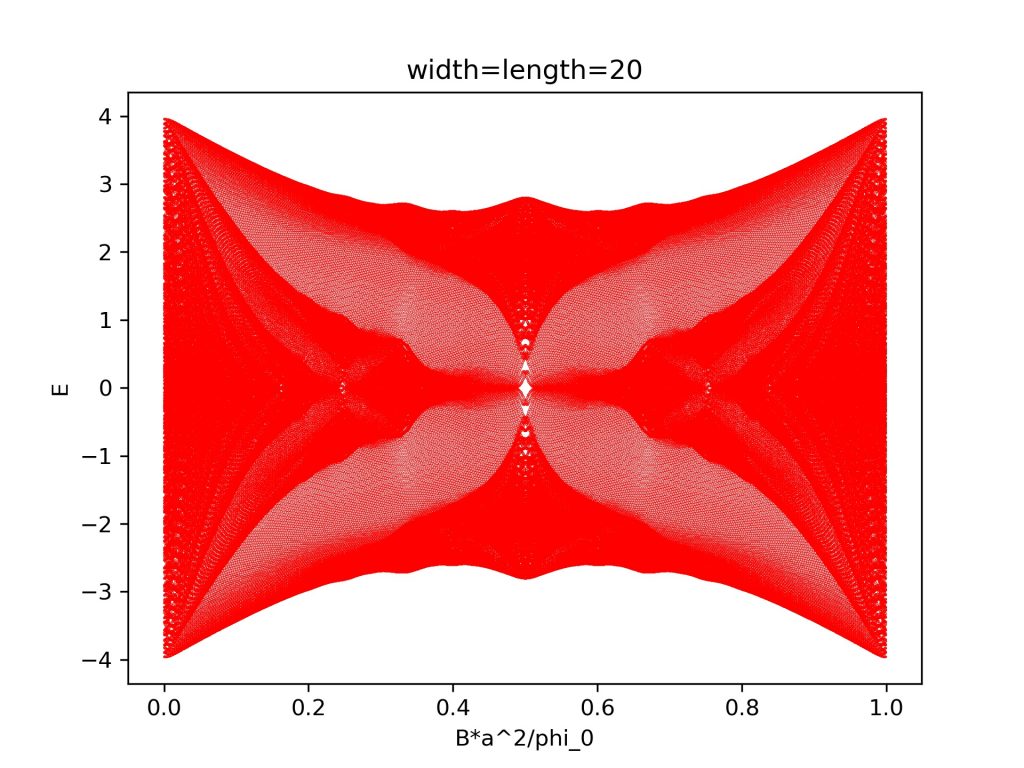
        plt.title('width=length='+str(n))
        plt.xlabel('B*a^2/phi_0')
        plt.ylabel('E')
        plt.savefig('width=length='+str(n)+'.jpg', dpi=300)
        plt.close('all')  # 关闭所有plt，防止循环画图时占用内存
        # plt.show()


def hamiltonian(width, length, B):   # 方格子哈密顿量
    h = np.zeros((width*length, width*length), dtype=complex)
    # y方向的跃迁
    for x in range(length):
        for y in range(width-1):
            h[x*width+y, x*width+y+1] = 1
            h[x*width+y+1, x*width+y] = 1
    # x方向的跃迁
    for x in range(length-1):
        for y in range(width):
            h[x*width+y, (x+1)*width+y] = 1*cmath.exp(-2*np.pi*1j*B*y)
            h[(x+1)*width+y, x*width+y] = 1*cmath.exp(2*np.pi*1j*B*y)
    return h


if __name__ == "__main__":
    main()

计算结果为：

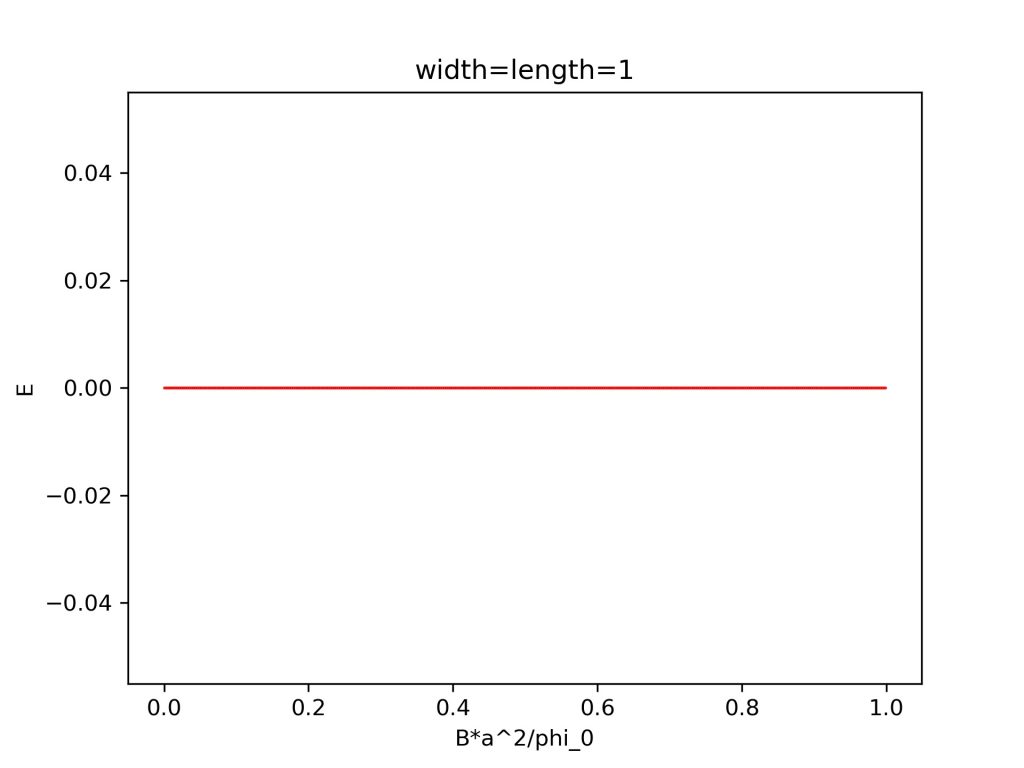
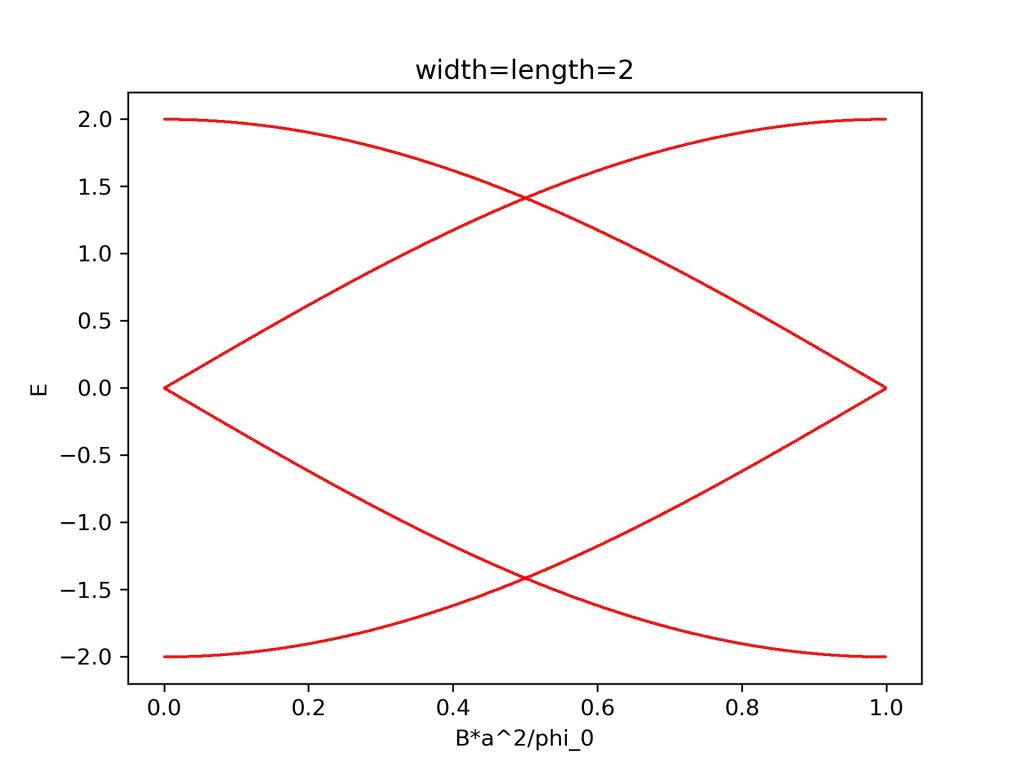
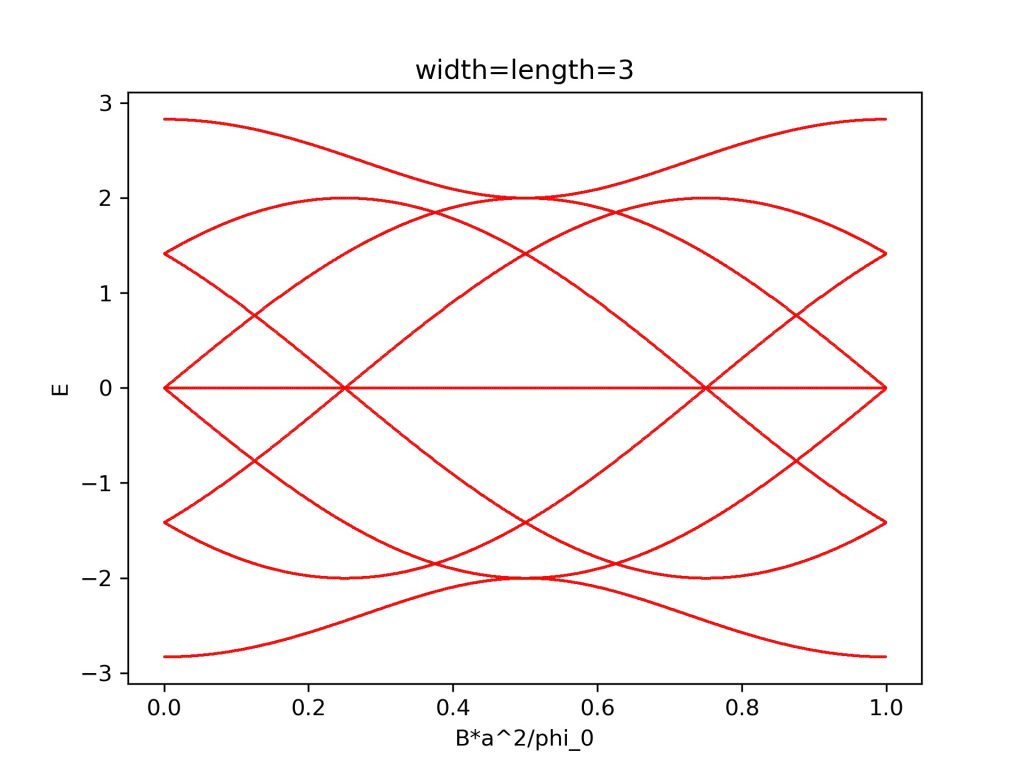
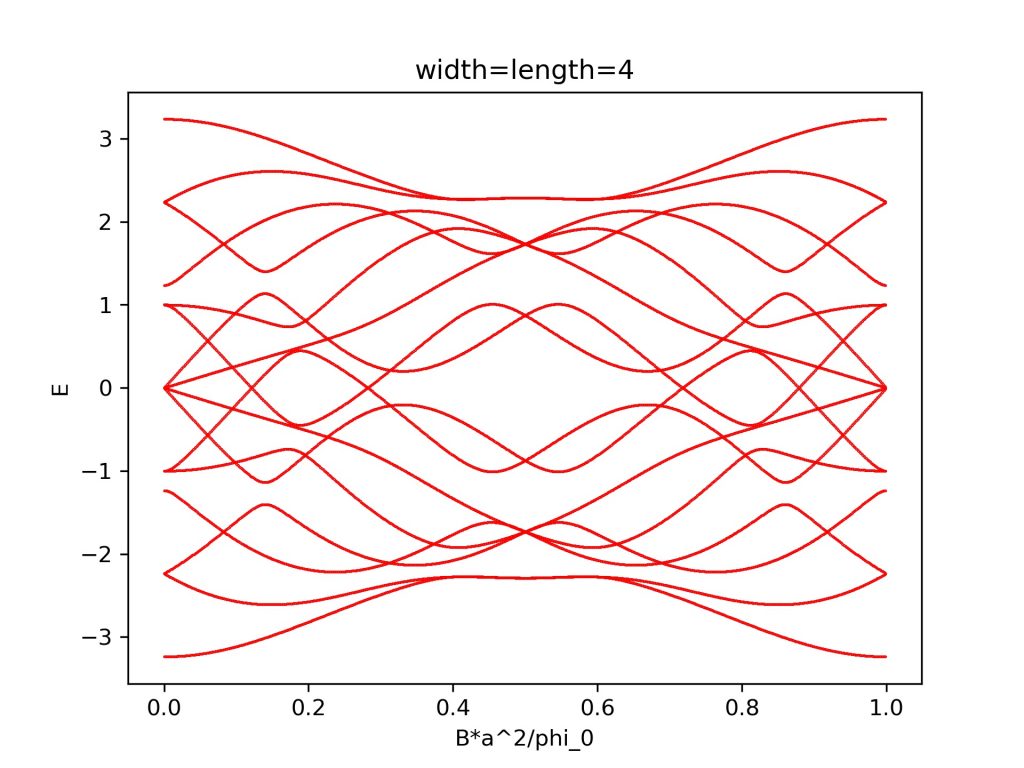
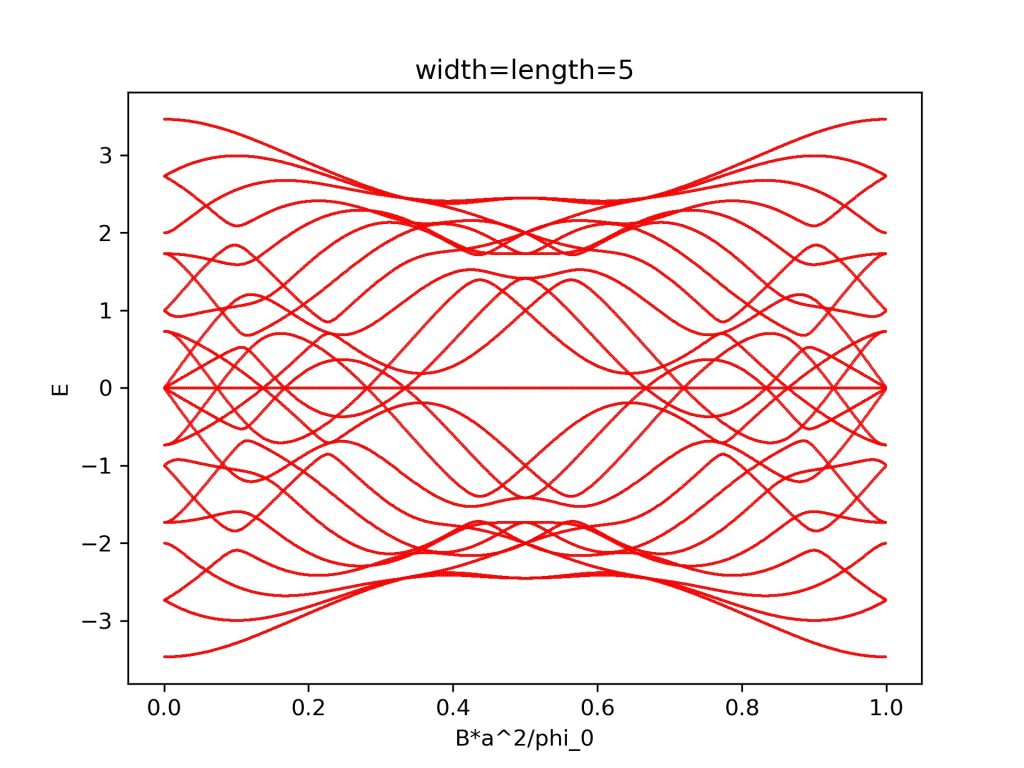
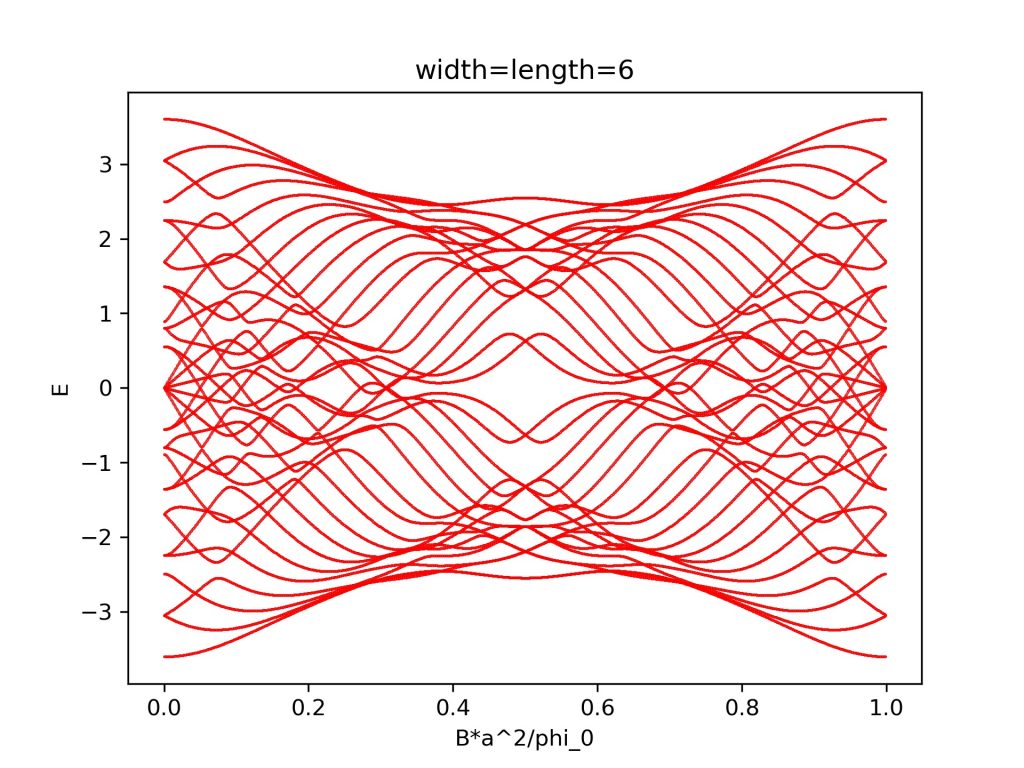
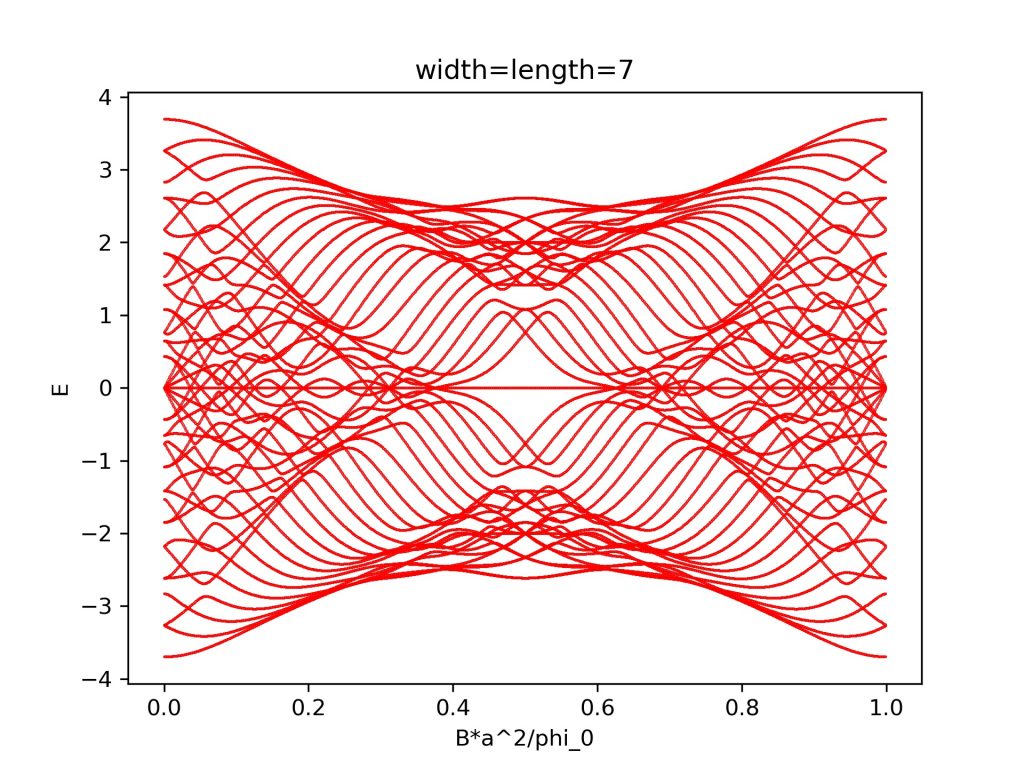
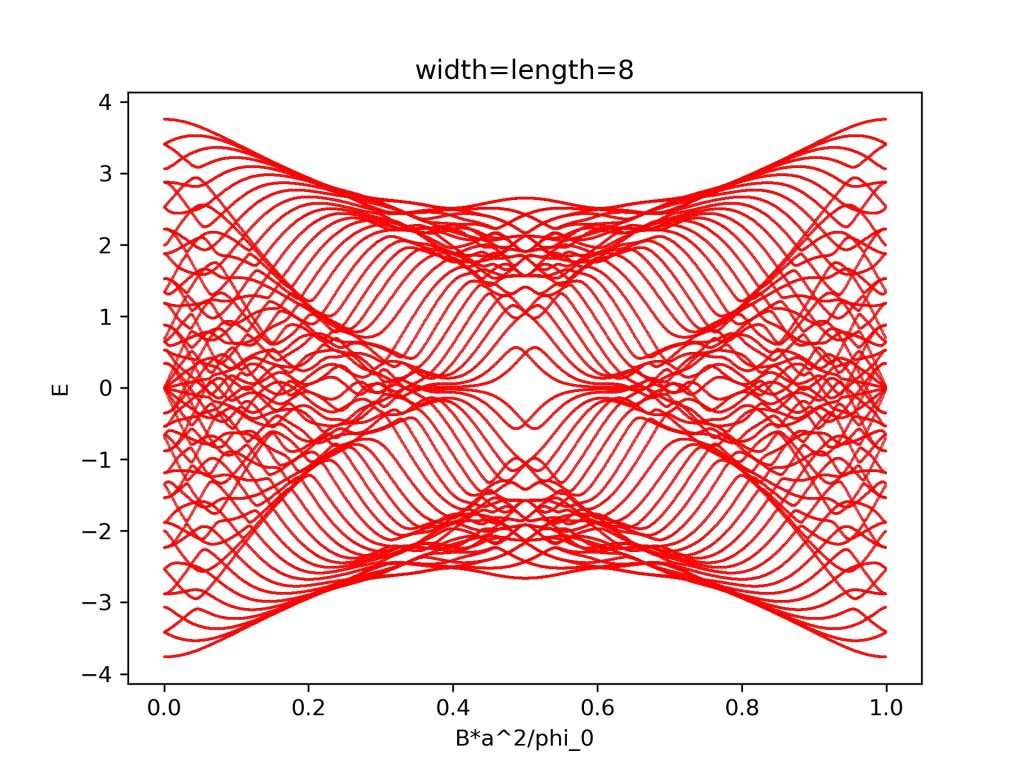
参考资料：

[1] Landau levels, molecular orbitals, and the Hofstadter butterfly in finite systems

[2] 知乎：二维方格Hofstadter's butterfly

[3] 知乎：什么是凝聚态中的 Hofstadter butterfly（霍夫斯塔特蝴蝶）？

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】