二维电子气的朗道能级

以二维电子气为例，哈密顿量为：

$H=\frac{p_x^2+p_y^2}{2m}$

磁场沿着 $z$ 方向，选取朗道规范（Landau gauge）：

$\overrightarrow{A}=(-By, 0, 0)$

加磁场后，薛定谔方程写为：

$\frac{(p_x+eBy)^2+p_y^2}{2m}\psi&=E\psi$

其中，算符:

$\begin{aligned} p_x&=-i\hbar\frac{\partial}{\partial x}\\p_y&=-i\hbar\frac{\partial}{\partial y}\end{aligned}$

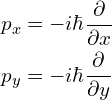
此外，波函数可以写为：

$\psi=e^{ikx}f(y)$

代入薛定谔方程，得到：

$\begin{aligned} \big[(-i\hbar \frac{\partial}{\partial x}+eBy )^{2}+(-i\hbar \frac{\partial}{\partial y})^{2}\big] e^{ikx}f(y) &=2mEe^{ikx}f(y)\\\big[-\hbar^2 \frac{\partial^2}{\partial y^2} + (\hbar k+eBy )^{2} \big] f(y) &=2mEf(y)\\\frac{\partial^2}{\partial y^2}f(y) +\big[ \frac{2mE}{\hbar^2}-\big(k+\frac{eBy}{\hbar}\big)^{2} \big] f(y) &=0\end{aligned}$

为了得到标准谐振子方程[2]：

$\frac{\partial ^2}{\partial \xi^2}f(\xi)+(\lambda-\xi^2})f(\xi)=0$

变量替换：

$\begin{aligned} \xi &= ay+b \\ \lambda&=cE \end{aligned}$

代入，得到：

$\begin{aligned} a^2\frac{\partial^2}{\partial \xi^2}f(\xi) +\big[ \frac{2m\frac{\lambda}{c}}{\hbar^2}-\big(k+\frac{eB\frac{\xi-b}{a}}{\hbar}\big)^{2} \big] f(\xi) &=0\\\frac{\partial^2}{\partial \xi^2}f(\xi) +\big\{\frac{2m\lambda}{\hbar^2 a^2 c}-\big[\frac{k}{a}+\frac{eB(\xi-b)}{\hbar a^2}\big]^{2} \big\} f(\xi) &=0\end{aligned}$

通过观察，参数选为：

$\begin{aligned} a&=\sqrt{\frac{eB}{\hbar}} \\ b&=\frac{k}{a}=\frac{k}{\sqrt{\frac{eB}{\hbar}}}\\c&=\frac{2m}{\hbar^2 a^2}=\frac{2m}{\hbar eB}\end{aligned}$

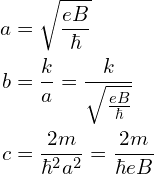
即变量替换为：

$\begin{aligned} \xi &= \sqrt{\frac{eB}{\hbar}}y+\frac{k}{\sqrt{\frac{eB}{\hbar}}} \\ \lambda&=\frac{2m}{\hbar eB}E\end{aligned}$

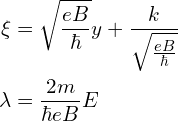
标准谐振子方程的解为[2]： $\lambda=2n+1$ ，即 $E=(2n+1)\frac{\hbar eB}{2m}$

令 $\omega = \frac{eB}{m}$ ，得到： $E=(n+\frac{1}{2})\hbar \omega$

$f(\xi)$ 用厄密多项式表示[2]： $f_{n}(\xi})=e^{-\frac{\xi^2}{2}}H_n(\xi)$

即 $f_{n}(y})=\mathrm{exp}\big[-\frac{1}{2} (\sqrt{\frac{eB}{\hbar}}y+\frac{k}{\sqrt{\frac{eB}{\hbar}}})^2\big]H_n\big(\sqrt{\frac{eB}{\hbar}}y+\frac{k}{\sqrt{\frac{eB}{\hbar}}}\big)$

因此，波函数写为： $\psi=e^{ikx}f(y)=\mathrm{exp}\big[ikx-\frac{1}{2} (\sqrt{\frac{eB}{\hbar}}y+\frac{k}{\sqrt{\frac{eB}{\hbar}}})^2\big]H_n\big(\sqrt{\frac{eB}{\hbar}}y+\frac{k}{\sqrt{\frac{eB}{\hbar}}}\big)$

此外，朗道能级还可以用粒子数算符来求解：用粒子数算符求解朗道能级。

参考资料：

[1] 广州大学Prof. Yanyang Zhang课堂笔记

[2] 季燕江《量子力学讲义》的4.2节、6.5节、8.3节

[3] Yan-Yang Zhang et al, Three-dimensional topological insulator in a magnetic field: chiral side surface states and quantized Hall conductance, J. Phys.: Condens. Matter 24 015004 (2012).

5,063 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】

3 thoughts on “二维电子气的朗道能级”

老师，我想问如果在谐振子基础上我希望y方向用一个有限大小，边界波函数为零的边界条件，我该怎么处理呢？

guanjihuan说道：

2025年3月10日 20:13

如果 y 方向为有限宽度，解析上可能很难处理，通常需要用数值方法来求解修正能级和波函数。方法可能是有限差分法、施加边界条件 ψ(y=0)=ψ(y=L)=0、本征值求解，但具体的计算方法我也不是很清楚，你可以找找教科书等资料，还有可以多问问 AI。

我猜大概的结论可能是：当宽度比较宽时，边界效应可忽略，朗道能级近似成立；当宽度接近于磁长度时，边界显著影响能级结构，且 y 方向的动量离散化。

回复
1. yizeroic说道：
  
  2025年3月11日 11:10
  
  谢谢老师
  
  回复

二维电子气的朗道能级

Published by guanjihuan

3 thoughts on “二维电子气的朗道能级”

发表评论取消回复

Published by guanjihuan

3 thoughts on “二维电子气的朗道能级”

发表评论 取消回复

发表评论取消回复