傅里叶变换:
![]()
反傅里叶变换:
![]()
1. 一维链的傅里叶变换过程
![Rendered by QuickLaTeX.com \begin{aligned}H&=\sum_{<x,x'>} t |x'\rangle \langle x| \\&=\sum_{x} \big( t |x+a\rangle \langle x| + \mathrm{H.c.} \big) \\&=\sum_{x} \big[ t \frac{1}{\sqrt{N}}\sum_{k}e^{ik'(x+a)}|k'\rangle \frac{1}{\sqrt{N}}\sum_{k}e^{-ikx}\langle k|+ \mathrm{H.c.}\big]\\&=\sum_{x} \big[ t\frac{1}{N}\sum_{k, k'}e^{i(k'-k)x+ik'a} |k'\rangle \langle k| + \mathrm{H.c.} \big]\\&=\sum_{k,k'} \big[ t e^{ik'a} \frac{1}{N}\sum_{x}e^{i(k'-k)x} |k'\rangle \langle k| + \mathrm{H.c.} \big]\\&=\sum_{k,k'} \big( t e^{ik'a} \delta_{k',k} |k'\rangle \langle k| + \mathrm{H.c.} \big) \\&=\sum_{k} \big( t e^{ika} |k\rangle \langle k| + \mathrm{H.c.} \big) \\&=\sum_{k} 2t\cos(ka) |k\rangle \langle k|\end{aligned}](https://www.guanjihuan.com/wp-content/ql-cache/quicklatex.com-9143b3fb33f7a82323923bc26938a420_l3.png)
2. 一维链的反傅里叶变换过程
![Rendered by QuickLaTeX.com \begin{aligned}&\quad \sum_{k}2t\cos(ka)|k\rangle\langle k| \\&=\sum_{k} t(e^{ika}+e^{-ika}) \frac{1}{\sqrt{N}}\sum_{x'}e^{-ikx'}|x'\rangle \frac{1}{\sqrt{N}}\sum_{x}e^{ikx}\langle x|\\&=\sum_{k} t(e^{ika}+e^{-ika})\frac{1}{N}\sum_{x,x'}e^{ik(x-x')}|x'\rangle\langle x| \\&=t \sum_{x,x'} [ \frac{1}{N} \sum_{k} (e^{ika}+e^{-ika}) e^{ik(x-x')} ] |x'\rangle \langle x| \\&=t \sum_{x,x'} [ \frac{1}{N} \sum_{k} e^{ik(x-x'+a)}+ \frac{1}{N} \sum_{k} e^{ik(x-x'-a)} ] |x'\rangle \langle x| \\&=t \sum_{x,x'} [\delta_{x+a,x'}+ \delta_{x, x'+a} ] |x'\rangle \langle x| \\&=t \sum_{<x,x'>} |x'\rangle \langle x|\end{ aligned }](https://www.guanjihuan.com/wp-content/ql-cache/quicklatex.com-999cd0865b09b6de57af08640b21cce8_l3.png)
3. 准一维条带(ribbon)的傅里叶变换过程
如果已知倒空间的哈密顿量,需要把k空间的哈密顿量反傅里叶变换到实空间中,得到跃迁项。而如果已知实空间的哈密顿量,那么就不用做这个步骤,直接可知跃迁项。
考虑准一维情况(有一定宽度,并且在某个方向上无限长),这时的元胞(最小重复单元)会变大。选定一组编号,把元胞当成整体,沿一个方向傅里叶变换(相当于沿一条链做傅里叶变换了),求本征值即可得到色散关系。
以准一维方格子为例,如下图所示:
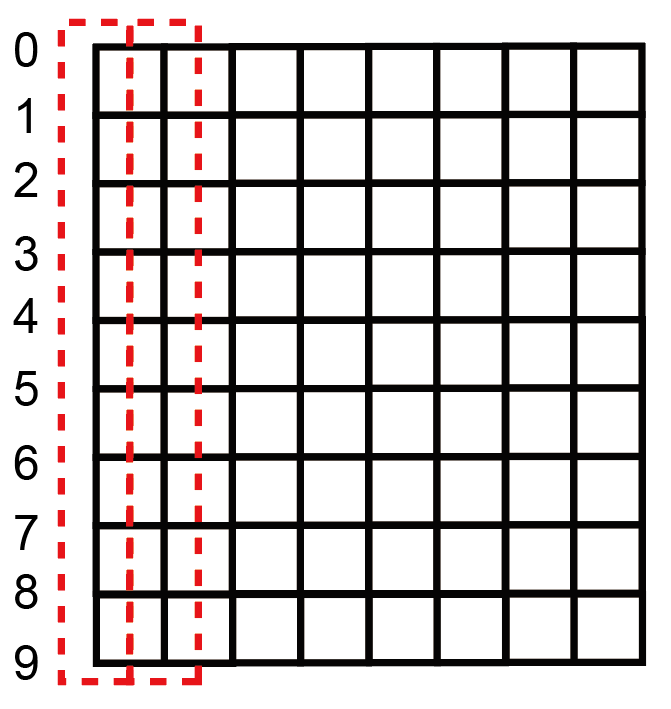
其中红色虚线包围的是最小重复单元(这里圈出两个元胞)。
傅里叶变换的具体过程如下(元胞间的跃迁矩阵为![]() ):
):
![Rendered by QuickLaTeX.com \begin{aligned}H&=\sum_{x} \big(H_{01} |x+a\rangle \langle x| + \mathrm{H.c.} \big) \\&=\sum_{x} \big[H_{01} \frac{1}{\sqrt{N}}\sum_{k}e^{ik'(x+a)}|k'\rangle \frac{1}{\sqrt{N}}\sum_{k}e^{-ikx}\langle k|+ \mathrm{H.c.}\big]\\&=\sum_{x} \big[ H_{01}\frac{1}{N}\sum_{k, k'}e^{i(k'-k)+ik'a} |k'\rangle \langle k| + \mathrm{H.c.} \big]\\&=\sum_{k,k'} \big[ H_{01} e^{ik'a} \frac{1}{N}\sum_{x}e^{i(k'-k)} |k'\rangle \langle k| + \mathrm{H.c.} \big]\\&=\sum_{k,k'} \big( H_{01} e^{ik'a} \delta_{k',k} |k'\rangle \langle k| + \mathrm{H.c.} \big) \\&=\sum_{k} \big( H_{01} e^{ika} |k\rangle \langle k| + \mathrm{H.c.} \big) \\&=\sum_{k}\big(H_{01} e^{ika}+H_{01}^{\dagger}e^{-ika} \big) |k\rangle \langle k|\end{aligned}](https://www.guanjihuan.com/wp-content/ql-cache/quicklatex.com-2662d27d4ad2942cee7213b0005f944e_l3.png)
如果![]() 为
为![]() ,则变回
,则变回![]() 的形式。
的形式。
此外,还要考虑元胞内部的哈密顿量![]() 。这里省略了过程,结果如下:
。这里省略了过程,结果如下:
![]()
代码例子:准一维方格子能带图(附Python代码)。
注:傅里叶变换时坐标可以用实际原子坐标,也可以用元胞坐标。用原子坐标时,傅里叶变量元胞内有些跃迁项会增加相位,即![]() ;而用元胞坐标时,傅里叶变换元胞内就没有增加相位,即
;而用元胞坐标时,傅里叶变换元胞内就没有增加相位,即![]() 。两种方法计算的结果是一样的,但建议用元胞坐标,会更方便些,尤其是当元胞比较大的时候会简单很多。 参考:以SSH模型为例子说明两种傅里叶变换方法。
。两种方法计算的结果是一样的,但建议用元胞坐标,会更方便些,尤其是当元胞比较大的时候会简单很多。 参考:以SSH模型为例子说明两种傅里叶变换方法。
4. 二维情况(两个方向上同时傅里叶变换)
(1) 正方格子哈密顿量的傅里叶变换

(2)石墨烯哈密顿量的傅里叶变换
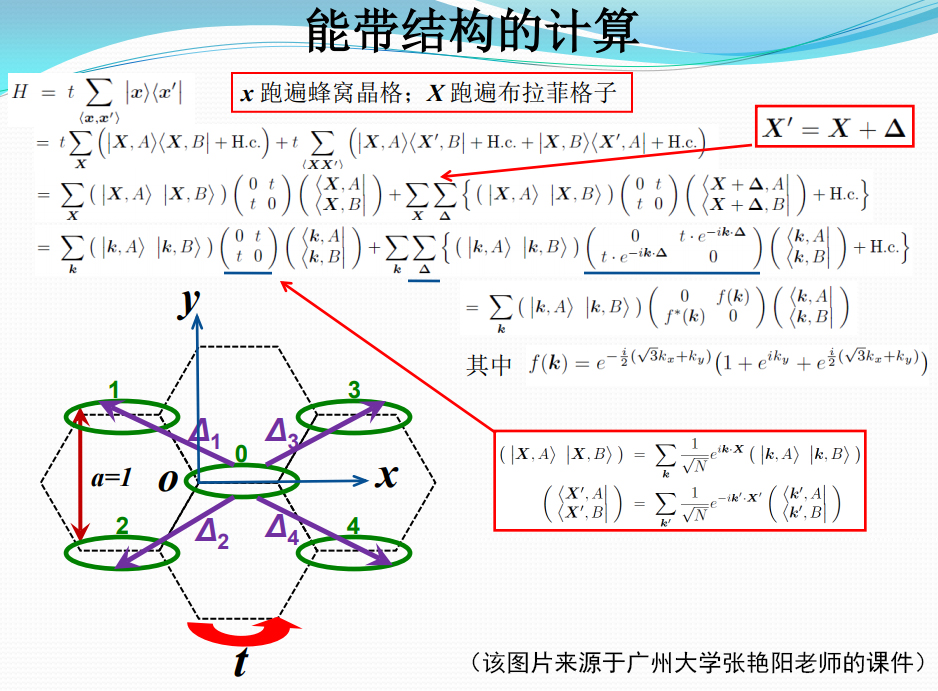
(课件截图上传已经征求原作者同意。课件的主要技术内容就这两页。)
5. 在离散晶格中傅里叶变换常见的形式
(1)最近邻跃迁
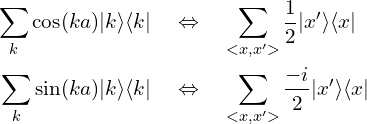
(2)次近邻跃迁:
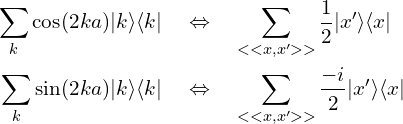
(3)斜对角跃迁:
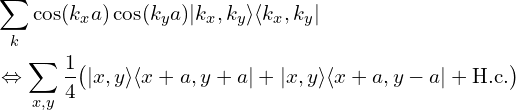
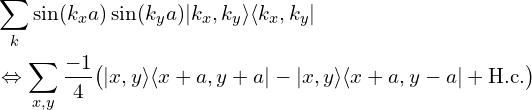
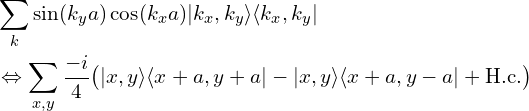
其他参考资料:
[2] Fourier Series, Fourier Transforms and the Delta Function
[3] Fourier transform 总结(新链接:https://zqw.ink/posts/2018-09-07-physics-Fourier%20transform%20总结.html,失效链接:https://zqw.ink/2018/09/07/Fourier transform 总结/)
[4] 六角蜂窝格子紧束缚模型的计算
[5] Ji-Huan Guan博士学位论文
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】
老师您好,请问能否发一下张老师的课件,谢谢!
已发至邮箱。
老师 您好,请问可以发一下张老师的课件吗。万分感激
已发至邮箱。
老师您好,如果出现cos(kx/2)cos(ky/2)该如何理解?
可以试着把原子间距当成 a=1/2 来处理。
老师您好,如果想要处理一个包含kx,ky,kz的三维动量空间哈密顿量,将其利用傅里叶变换转到实空间,在此过程中是否可以将kz看作体系参数保留k空间的形式,从而把三维哈密顿量等效为二维有效哈密顿量
如果把kz作为参数,kx和ky作为维度,那么是可以看做是包含kz参数的二维哈密顿量,但这个形式和三维哈密顿量是一样的。
如果把kx和ky反傅里叶变换到实空间,x和y方向取有限宽度,然后保留kz,那么是准一维的哈密顿量(tube),沿着z方向。
老师,可以发一下张艳杨老师的课件吗
已发
呜呜,老师您如果方便的话,能不能也发我一份呢?您的资料对我太有帮助了呢^^ 总之谢谢您的分享~
如果方便的话
手动爱心
已发。
关老师您好,可以分享一下张艳阳老师的课件吗,如果时间太久您那里也没有了也,没关系,您的文章对我的帮助很大,非常感谢您
已发送。
收到了,感谢关老师
关老师,您的参考文献3傅里叶总结打不开,有新的链接吗?
嗯,对方博客更新,原链接失效了。新链接是:https://zqw.ink/posts/2018-09-07-physics-Fourier%20transform%20总结.html
关老师,也求一份课件,谢谢????
已发至邮箱。
收到,谢谢关老师
如果对正方格子这个模型稍加变化,四个格点组成的不是正方了,而是个斜的平行四边形,向下的跃迁还能标志成y到y+1吗
还是可以的表示的。只是可能跃迁积分会发生变化,或者傅里叶变换后包含kx和ky的形式不一样
关老师,为什么第一个正方格子那个格点没有考虑向左和向上的跃迁呢
不好意思,漏看了,应该是在厄米共轭里
是的
博主,你好。我想问一下:a.算石墨烯那一页第四个等号右边的第二项是胞间跃迁吧,那在考虑胞间跃迁的时,是以原胞整体考虑吗?还是一个原子一个原子的看,看它们能跃迁到另一个原胞的哪个位置。b.按照图示,胞间跃迁有四项,那f(k)不是应该也有四项吗。如果您太忙没时间解答,请略过呀。谢谢~
(a)是的,是胞间跃迁,这里是以整体做的傅里叶变换。当然,你也可以按原子来做傅里叶变换。(b)H.c. 表示厄密共轭,包含了另外两项。总共四项。
博主,你好!我想问一下,这个胞间跃迁是不是有重复求和啊
没有重复求和。A到B的跃迁、B到A的跃迁(由厄米共轭 H.c. 来表示)属于两个不同的跃迁。最终的哈密顿量是厄米的。
老师,麻烦您分享以下张老师的课件用于学习可以吗?谢谢老师啦!
已发
请问在哪可以看到呀?我也想学习。谢谢????
已发至你邮箱。
老师,张老师的课件可以分享一下吗
已发。
关博士您好,请问可以发一下张老师的课件吗。万分感激。
已发。
老师您好,可以分享一下张艳阳老师的课件吗,谢谢啦
已发。
老师,您好,可以分享一下张艳阳老师的课件吗,感谢感谢
已发。
请问老师,一维傅里叶变换最后一步那个2应该不写才对吧?
要写的呀。H.c.表示厄密共轭。于是有:exp(ikx)+exp(-ikx)=2cos(kx)
谢谢关老师
老师您好,可以分享一下张艳阳老师的课件吗,谢谢啦
已发。
可以的话能分享一下张老师课件吗,麻烦啦
另外笔记中石墨烯部分似乎有些问题,不过还是能看明白的
嗯,已发。大概思路是没问题的,可能表述和理解有差异。
老师您好,能发下张艳阳老师的课件吗
已发。
老师您好,请问可以分享一下张艳阳老师的课件吗?谢谢您~
已发。
老师您好,可以分享一下张艳阳老师的课件吗,谢谢啦
已发。