补充说明:除了本篇的计算方法,还有另外一种比本篇更加简单的算法(由zhangjiayan同学提供),思想是把每一层左右两侧都当成自能。该算法的代码可以参考这篇:使用Dyson方程计算格林函数的对角分块矩阵(第二种方法)。公式参考书籍“2016 - Ryndyk - Theory of Quantum Transport at Nanoscale”的(3.152)式:
![]()
此外也可以阅读这几篇:
- 方格子模型在实空间中的哈密顿量形式
- 格林函数中Dyson方程的数值验证(附Python代码)
- 数值验证“波函数模平方分布”和“态密度分布”的关系(附Python代码)
- 方格子和石墨烯的态密度与费米能的关系(附Python代码)
- 非平衡格林函数计算电导(附Python代码)
在计算电导时,我们只需要知道格林函数右上角的一个分块矩阵![]() 。在计算态密度公式中,我们需要知道格林函数对角线上的元素,因此需要计算出格林函数所有的对角分块矩阵
。在计算态密度公式中,我们需要知道格林函数对角线上的元素,因此需要计算出格林函数所有的对角分块矩阵![]() ,
,![]() ,
,![]() ……
……
本篇通过不断套用 Dyson 方程,计算格林函数的对角分块矩阵,进而计算出态密度。考虑的体系是有限长宽的方格子。用上 Dyson 方程后计算的矩阵维度可以大幅度降低,矩阵维度从 width*length 下降到 width。
戴森方程(Dyson equation) 为[1]:
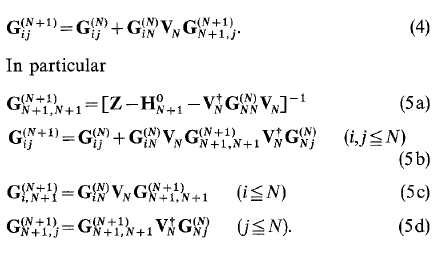
计算![]() 具体公式可以写为:
具体公式可以写为:
![Rendered by QuickLaTeX.com \begin{aligned}G_{11}^{(1)}&=[(E+i\eta)I-H_{11}]^{-1}\\G_{12}^{(2)}&=G_{11}^{(1)}V_{12}G_{22}^{(2)}\\G_{13}^{(3)}&=G_{12}^{(2)}V_{23}G_{33}^{(3)}\\&\quad\quad......\end{aligned}](https://www.guanjihuan.com/wp-content/ql-cache/quicklatex.com-bead90cb1294a9867862a59ffde3d403_l3.png)
其中,
![Rendered by QuickLaTeX.com \begin{aligned}G_{22}^{(2)}&=[(E+i\eta)I-H_{22}-V_{12}^{\dagger}G_{11}^{(1)}V_{12}]^{-1}\\G_{33}^{(3)}&=[(E+i\eta)I-H_{33}-V_{23}^{\dagger}G_{22}^{(2)}V_{23}]^{-1}\\&\quad\quad\quad\quad\quad\quad......\end{aligned}](https://www.guanjihuan.com/wp-content/ql-cache/quicklatex.com-aba242626a1d54025f05e1fc30177001_l3.png)
通常,![]() ,
,![]() 。
。
此外,如果考虑了左电极的自能![]() ,则
,则![]()
需要说明的是:格林函数![]() 的右上角括号(x)表示当前的体系大小。因此,这里的
的右上角括号(x)表示当前的体系大小。因此,这里的![]() ,
,![]() ,
,![]() ……不是计算态密度所需要的对角分块矩阵。我们需要的是
……不是计算态密度所需要的对角分块矩阵。我们需要的是![]() ,
,![]() ,
,![]() ……其中,(n)表示需要计算的体系大小。
……其中,(n)表示需要计算的体系大小。
下面给出具体的表达式:
![Rendered by QuickLaTeX.com \begin{aligned}G_{11}^{(1)}&=[(E+i\eta)I-H_{11}]^{-1}\\G_{11}^{(2)}&=G_{11}^{(1)}+G_{11}^{(1)}V_{12}G_{22}^{(2)}V_{12}^{\dagger}G_{11}^{(1)}\\G_{11}^{(3)}&=G_{11}^{(2)}+G_{12}^{(2)}V_{23}G_{33}^{(3)}V_{23}^{\dagger}G_{21}^{(2)}\\G_{11}^{(4)}&=G_{11}^{(3)}+G_{13}^{(3)}V_{34}G_{44}^{(4)}V_{34}^{\dagger}G_{31}^{(3)}\\&\quad\quad\quad\quad......\end{aligned}](https://www.guanjihuan.com/wp-content/ql-cache/quicklatex.com-a3d08b01c14ef8687199e7b233311039_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned}G_{22}^{(2)}&=[(E+i\eta)I-H_{22}-V_{12}^{\dagger}G_{11}^{(1)}V_{12}]^{-1}\\G_{22}^{(3)}&=G_{22}^{(2)}+G_{22}^{(2)}V_{23}G_{33}^{(3)}V_{23}^{\dagger}G_{22}^{(2)}\\G_{22}^{(4)}&=G_{22}^{(3)}+G_{23}^{(3)}V_{34}G_{44}^{(4)}V_{34}^{\dagger}G_{32}^{(3)}\\G_{22}^{(5)}&=G_{22}^{(4)}+G_{24}^{(4)}V_{45}G_{55}^{(5)}V_{45}^{\dagger}G_{42}^{(3)}\\&\quad\quad\quad\quad\quad......\end{aligned}](https://www.guanjihuan.com/wp-content/ql-cache/quicklatex.com-e4991294f4fdd27b10431a0985d43b8d_l3.png)
其中,
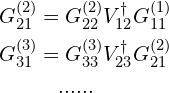
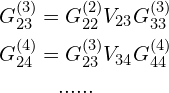
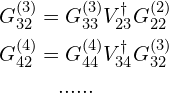
同理有![]() ,
,![]() ,
,![]() 等。上面的表达式看起来虽然复杂,但都只是在套用 Dyson 方程的表达式。
等。上面的表达式看起来虽然复杂,但都只是在套用 Dyson 方程的表达式。
一、方格子
Python 代码如下:
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/7650
"""
import numpy as np
def matrix_00(width):
h00 = np.zeros((width, width))
for width0 in range(width-1):
h00[width0, width0+1] = 1
h00[width0+1, width0] = 1
return h00
def matrix_01(width):
h01 = np.identity(width)
return h01
def main():
width = 2
length = 3
eta = 1e-2
E = 0
h00 = matrix_00(width)
h01 = matrix_01(width)
G_ii_n_array = G_ii_n_with_Dyson_equation(width, length, E, eta, h00, h01)
for i0 in range(length):
# print('G_{'+str(i0+1)+','+str(i0+1)+'}^{('+str(length)+')}:')
# print(G_ii_n_array[i0, :, :],'\n')
print('x=', i0+1, ':')
for j0 in range(width):
print(' y=', j0+1, ' ', -np.imag(G_ii_n_array[i0, j0, j0])/np.pi) # 态密度
def G_ii_n_with_Dyson_equation(width, length, E, eta, h00, h01):
G_ii_n_array = np.zeros((length, width, width), complex)
G_11_1 = np.linalg.inv((E+eta*1j)*np.identity(width)-h00)
for i in range(length): # i为格林函数的右下指标
# 初始化开始
G_nn_n_minus = G_11_1
G_in_n_minus = G_11_1
G_ni_n_minus = G_11_1
G_ii_n_minus = G_11_1
for i0 in range(i):
G_nn_n = Green_nn_n(E, eta, h00, h01, G_nn_n_minus)
G_nn_n_minus = G_nn_n
if i!=0:
G_in_n_minus = G_nn_n
G_ni_n_minus = G_nn_n
G_ii_n_minus = G_nn_n
# 初始化结束
for j0 in range(length-1-i): # j0为格林函数的右上指标,表示当前体系大小,即G^{(j0)}
G_nn_n = Green_nn_n(E, eta, h00, h01, G_nn_n_minus)
G_nn_n_minus = G_nn_n
G_ii_n = Green_ii_n(G_ii_n_minus, G_in_n_minus, h01, G_nn_n, G_ni_n_minus) # 需要求的对角分块矩阵
G_ii_n_minus = G_ii_n
G_in_n = Green_in_n(G_in_n_minus, h01, G_nn_n)
G_in_n_minus = G_in_n
G_ni_n = Green_ni_n(G_nn_n, h01, G_ni_n_minus)
G_ni_n_minus = G_ni_n
G_ii_n_array[i, :, :] = G_ii_n_minus
return G_ii_n_array
def Green_nn_n(E, eta, H00, V, G_nn_n_minus): # n>=2
dim = H00.shape[0]
G_nn_n = np.linalg.inv((E+eta*1j)*np.identity(dim)-H00-np.dot(np.dot(V.transpose().conj(), G_nn_n_minus), V))
return G_nn_n
def Green_in_n(G_in_n_minus, V, G_nn_n): # n>=2
G_in_n = np.dot(np.dot(G_in_n_minus, V), G_nn_n)
return G_in_n
def Green_ni_n(G_nn_n, V, G_ni_n_minus): # n>=2
G_ni_n = np.dot(np.dot(G_nn_n, V.transpose().conj()), G_ni_n_minus)
return G_ni_n
def Green_ii_n(G_ii_n_minus, G_in_n_minus, V, G_nn_n, G_ni_n_minus): # n>=i
G_ii_n = G_ii_n_minus+np.dot(np.dot(np.dot(np.dot(G_in_n_minus, V), G_nn_n), V.transpose().conj()),G_ni_n_minus)
return G_ii_n
if __name__ == '__main__':
main()
计算结果为:
x= 1 :
y= 1 0.006363334525329511
y= 2 0.006363334525331773
x= 2 :
y= 1 0.009543888466882358
y= 2 0.009543888466880096
x= 3 :
y= 1 0.006363334525330208
y= 2 0.00636333452533021为了验证以上代码和计算结果的正确性,下面用传统直接求逆的方法计算态密度。计算的体系也是方格子。代码如下:
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/7650
"""
import numpy as np
def hamiltonian(width, length):
h = np.zeros((width*length, width*length))
for i0 in range(length):
for j0 in range(width-1):
h[i0*width+j0, i0*width+j0+1] = 1
h[i0*width+j0+1, i0*width+j0] = 1
for i0 in range(length-1):
for j0 in range(width):
h[i0*width+j0, (i0+1)*width+j0] = 1
h[(i0+1)*width+j0, i0*width+j0] = 1
return h
def main():
width = 2
length = 3
h = hamiltonian(width, length)
E = 0
green = np.linalg.inv((E+1e-2j)*np.eye(width*length)-h)
for i0 in range(length):
# print('G_{'+str(i0+1)+','+str(i0+1)+'}^{('+str(length)+')}:')
# print(green[i0*width+0: i0*width+width, i0*width+0: i0*width+width], '\n')
print('x=', i0+1, ':')
for j0 in range(width):
print(' y=', j0+1, ' ', -np.imag(green[i0*width+j0, i0*width+j0])/np.pi)
if __name__ == "__main__":
main()
计算结果为:
x= 1 :
y= 1 0.00636333452533021
y= 2 0.00636333452533021
x= 2 :
y= 1 0.00954388846688089
y= 2 0.00954388846688089
x= 3 :
y= 1 0.00636333452533021
y= 2 0.00636333452533021结果在误差范围内是相等的。
二、立方格子
把每一层切片当成一个单元,进行 Dyson 方程的迭代。代码为:
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/7650
"""
import numpy as np
def matrix_00(width, length):
h00 = np.zeros((width*length, width*length))
for x in range(length):
for y in range(width-1):
h00[x*width+y, x*width+y+1] = 1
h00[x*width+y+1, x*width+y] = 1
for x in range(length-1):
for y in range(width):
h00[x*width+y, (x+1)*width+y] = 1
h00[(x+1)*width+y, x*width+y] = 1
return h00
def matrix_01(width, length):
h01 = np.identity(width*length)
return h01
def main():
height = 2 # z
width = 3 # y
length = 4 # x
eta = 1e-2
E = 0
h00 = matrix_00(width, length)
h01 = matrix_01(width, length)
G_ii_n_array = G_ii_n_with_Dyson_equation(width, length, height, E, eta, h00, h01)
for i0 in range(height):
print('z=', i0+1, ':')
for j0 in range(width):
print(' y=', j0+1, ':')
for k0 in range(length):
print(' x=', k0+1, ' ', -np.imag(G_ii_n_array[i0, k0*width+j0, k0*width+j0])/np.pi) # 态密度
def G_ii_n_with_Dyson_equation(width, length, height, E, eta, h00, h01):
dim = length*width
G_ii_n_array = np.zeros((height, dim, dim), dtype=complex)
G_11_1 = np.linalg.inv((E+eta*1j)*np.identity(dim)-h00)
for i in range(height): # i为格林函数的右下指标
# 初始化开始
G_nn_n_minus = G_11_1
G_in_n_minus = G_11_1
G_ni_n_minus = G_11_1
G_ii_n_minus = G_11_1
for i0 in range(i):
G_nn_n = Green_nn_n(E, eta, h00, h01, G_nn_n_minus)
G_nn_n_minus = G_nn_n
if i!=0:
G_in_n_minus = G_nn_n
G_ni_n_minus = G_nn_n
G_ii_n_minus = G_nn_n
# 初始化结束
for j0 in range(height-1-i): # j0为格林函数的右上指标,表示当前体系大小,即G^{(j0)}
G_nn_n = Green_nn_n(E, eta, h00, h01, G_nn_n_minus)
G_nn_n_minus = G_nn_n
G_ii_n = Green_ii_n(G_ii_n_minus, G_in_n_minus, h01, G_nn_n, G_ni_n_minus) # 需要求的对角分块矩阵
G_ii_n_minus = G_ii_n
G_in_n = Green_in_n(G_in_n_minus, h01, G_nn_n)
G_in_n_minus = G_in_n
G_ni_n = Green_ni_n(G_nn_n, h01, G_ni_n_minus)
G_ni_n_minus = G_ni_n
G_ii_n_array[i, :, :] = G_ii_n_minus
return G_ii_n_array
def Green_nn_n(E, eta, H00, V, G_nn_n_minus): # n>=2
dim = H00.shape[0]
G_nn_n = np.linalg.inv((E+eta*1j)*np.identity(dim)-H00-np.dot(np.dot(V.transpose().conj(), G_nn_n_minus), V))
return G_nn_n
def Green_in_n(G_in_n_minus, V, G_nn_n): # n>=2
G_in_n = np.dot(np.dot(G_in_n_minus, V), G_nn_n)
return G_in_n
def Green_ni_n(G_nn_n, V, G_ni_n_minus): # n>=2
G_ni_n = np.dot(np.dot(G_nn_n, V.transpose().conj()), G_ni_n_minus)
return G_ni_n
def Green_ii_n(G_ii_n_minus, G_in_n_minus, V, G_nn_n, G_ni_n_minus): # n>=i
G_ii_n = G_ii_n_minus+np.dot(np.dot(np.dot(np.dot(G_in_n_minus, V), G_nn_n), V.transpose().conj()),G_ni_n_minus)
return G_ii_n
if __name__ == '__main__':
main()计算结果为:
z= 1 :
y= 1 :
x= 1 0.012359150296950887
x= 2 0.00671198877108385
x= 3 0.006711988771083864
x= 4 0.012359150296950897
y= 2 :
x= 1 0.015174729801012383
x= 2 0.007060642985111396
x= 3 0.007060642985111418
x= 4 0.01517472980101239
y= 3 :
x= 1 0.0123591502969509
x= 2 0.0067119887710838586
x= 3 0.006711988771083864
x= 4 0.0123591502969509
z= 2 :
y= 1 :
x= 1 0.0123591502969509
x= 2 0.006711988771083854
x= 3 0.006711988771083854
x= 4 0.012359150296950889
y= 2 :
x= 1 0.015174729801012383
x= 2 0.007060642985111406
x= 3 0.007060642985111405
x= 4 0.015174729801012376
y= 3 :
x= 1 0.012359150296950892
x= 2 0.006711988771083858
x= 3 0.006711988771083852
x= 4 0.012359150296950894用传统直接求逆的方法计算态密度进行验证,代码为:
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/7650
"""
import numpy as np
def hamiltonian(width, length, height):
h = np.zeros((width*length*height, width*length*height))
for i0 in range(length):
for j0 in range(width):
for k0 in range(height-1):
h[k0*width*length+i0*width+j0, (k0+1)*width*length+i0*width+j0] = 1
h[(k0+1)*width*length+i0*width+j0, k0*width*length+i0*width+j0] = 1
for i0 in range(length):
for j0 in range(width-1):
for k0 in range(height):
h[k0*width*length+i0*width+j0, k0*width*length+i0*width+j0+1] = 1
h[k0*width*length+i0*width+j0+1, k0*width*length+i0*width+j0] = 1
for i0 in range(length-1):
for j0 in range(width):
for k0 in range(height):
h[k0*width*length+i0*width+j0, k0*width*length+(i0+1)*width+j0] = 1
h[k0*width*length+(i0+1)*width+j0, k0*width*length+i0*width+j0] = 1
return h
def main():
height = 2 # z
width = 3 # y
length = 4 # x
h = hamiltonian(width, length, height)
E = 0
green = np.linalg.inv((E+1e-2j)*np.eye(width*length*height)-h)
for k0 in range(height):
print('z=', k0+1, ':')
for j0 in range(width):
print(' y=', j0+1, ':')
for i0 in range(length):
print(' x=', i0+1, ' ', -np.imag(green[k0*width*length+i0*width+j0, k0*width*length+i0*width+j0])/np.pi) # 态密度
if __name__ == "__main__":
main()计算结果为:
z= 1 :
y= 1 :
x= 1 0.012359150296950895
x= 2 0.006711988771083862
x= 3 0.006711988771083851
x= 4 0.012359150296950895
y= 2 :
x= 1 0.015174729801012378
x= 2 0.007060642985111408
x= 3 0.00706064298511141
x= 4 0.01517472980101238
y= 3 :
x= 1 0.012359150296950894
x= 2 0.006711988771083856
x= 3 0.00671198877108385
x= 4 0.012359150296950894
z= 2 :
y= 1 :
x= 1 0.012359150296950895
x= 2 0.006711988771083847
x= 3 0.0067119887710838525
x= 4 0.012359150296950895
y= 2 :
x= 1 0.015174729801012376
x= 2 0.007060642985111405
x= 3 0.007060642985111409
x= 4 0.01517472980101238
y= 3 :
x= 1 0.012359150296950897
x= 2 0.006711988771083851
x= 3 0.006711988771083855
x= 4 0.012359150296950895结果在误差范围内是一致的。
另外,下面把利用 Dyson 方程迭代方法计算态密度(立方格子)的代码做了一些细节上的修改,这里称为第二版本“version II",主要是删除 G_ii_n_array 这个变量,因为这个变量太占内存了。经过处理后,在有限的内存下,能够计算的体系大小会更大一些,消耗的内存降低为 1/height 倍的量级。
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/7650
"""
import numpy as np
def matrix_00(width, length):
h00 = np.zeros((width*length, width*length))
for x in range(length):
for y in range(width-1):
h00[x*width+y, x*width+y+1] = 1
h00[x*width+y+1, x*width+y] = 1
for x in range(length-1):
for y in range(width):
h00[x*width+y, (x+1)*width+y] = 1
h00[(x+1)*width+y, x*width+y] = 1
return h00
def matrix_01(width, length):
h01 = np.identity(width*length)
return h01
def main():
height = 2 # z
width = 3 # y
length = 4 # x
eta = 1e-2
E = 0
h00 = matrix_00(width, length)
h01 = matrix_01(width, length)
G_ii_n_with_Dyson_equation_version_II(width, length, height, E, eta, h00, h01)
def G_ii_n_with_Dyson_equation_version_II(width, length, height, E, eta, h00, h01):
dim = length*width
G_11_1 = np.linalg.inv((E+eta*1j)*np.identity(dim)-h00)
for i in range(height): # i为格林函数的右下指标
# 初始化开始
G_nn_n_minus = G_11_1
G_in_n_minus = G_11_1
G_ni_n_minus = G_11_1
G_ii_n_minus = G_11_1
for i0 in range(i):
G_nn_n = Green_nn_n(E, eta, h00, h01, G_nn_n_minus)
G_nn_n_minus = G_nn_n
if i!=0:
G_in_n_minus = G_nn_n
G_ni_n_minus = G_nn_n
G_ii_n_minus = G_nn_n
# 初始化结束
for j0 in range(height-1-i): # j0为格林函数的右上指标,表示当前体系大小,即G^{(j0)}
G_nn_n = Green_nn_n(E, eta, h00, h01, G_nn_n_minus)
G_nn_n_minus = G_nn_n
G_ii_n = Green_ii_n(G_ii_n_minus, G_in_n_minus, h01, G_nn_n, G_ni_n_minus) # 需要求的对角分块矩阵
G_ii_n_minus = G_ii_n
G_in_n = Green_in_n(G_in_n_minus, h01, G_nn_n)
G_in_n_minus = G_in_n
G_ni_n = Green_ni_n(G_nn_n, h01, G_ni_n_minus)
G_ni_n_minus = G_ni_n
# 输出
print('z=', i+1, ':')
for j0 in range(width):
print(' y=', j0+1, ':')
for k0 in range(length):
print(' x=', k0+1, ' ', -np.imag(G_ii_n_minus[k0*width+j0, k0*width+j0])/np.pi) # 态密度
def Green_nn_n(E, eta, H00, V, G_nn_n_minus): # n>=2
dim = H00.shape[0]
G_nn_n = np.linalg.inv((E+eta*1j)*np.identity(dim)-H00-np.dot(np.dot(V.transpose().conj(), G_nn_n_minus), V))
return G_nn_n
def Green_in_n(G_in_n_minus, V, G_nn_n): # n>=2
G_in_n = np.dot(np.dot(G_in_n_minus, V), G_nn_n)
return G_in_n
def Green_ni_n(G_nn_n, V, G_ni_n_minus): # n>=2
G_ni_n = np.dot(np.dot(G_nn_n, V.transpose().conj()), G_ni_n_minus)
return G_ni_n
def Green_ii_n(G_ii_n_minus, G_in_n_minus, V, G_nn_n, G_ni_n_minus): # n>=i
G_ii_n = G_ii_n_minus+np.dot(np.dot(np.dot(np.dot(G_in_n_minus, V), G_nn_n), V.transpose().conj()),G_ni_n_minus)
return G_ii_n
if __name__ == '__main__':
main()参考资料:
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】