在这篇文章“陈数Chern number的计算(定义法,附Python/Matlab代码)”中,由于模型比较简单,数值上波函数恰好为同一个规范。然而大部分的时候,当选取不同的k值时,波函数的规范不一定保持一致,这是由于改变规范,波函数仍然是哈密顿量的解:
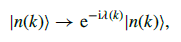
这时候可以采用二分查找的方法在数值上寻找波函数近似的同一规范。此外还可以固定某一个规范,参考这篇中的代码:SSH模型中的wilson loop(附Python代码)。本篇给出的是二分查找的方法。
以下对“陈数Chern number的计算(定义法,附Python/Matlab代码)”这篇中的代码做测试。选取积分密度为n = 100,计算结果为:
Chern number = (2.0000002869141356-4.9548136005219324e-09j)
测试1:同时改变规范
这里需要python库:import cmath
同时改变规范cmath.exp(-1j*1)
vector = vector*cmath.exp(-1j*1)
vector_delta_kx = vector_delta_kx*cmath.exp(-1j*1)
vector_delta_ky = vector_delta_ky*cmath.exp(-1j*1)
vector_delta_kx_ky = vector_delta_kx_ky*cmath.exp(-1j*1)计算结果为:
Chern number = (2.0000002884971892-5.666151182275949e-09j)
结果基本上保持不变。
测试2:某个波函数略微偏离规范,偏离1e-8
vector = vector*cmath.exp(-1j*1)
vector_delta_kx = vector_delta_kx*cmath.exp(-1j*1)
vector_delta_ky = vector_delta_ky*cmath.exp(-1j*1)
vector_delta_kx_ky = vector_delta_kx_ky*cmath.exp(-1j*(1+1e-8))计算结果为:
Chern number = (2.0000004097702826+0.02325606251939269j)
结果是实部值基本上不变,虚部值变化一点点。
测试3:某个波函数略微偏离规范,偏离1e-4
vector = vector*cmath.exp(-1j*1)
vector_delta_kx = vector_delta_kx*cmath.exp(-1j*1)
vector_delta_ky = vector_delta_ky*cmath.exp(-1j*1)
vector_delta_kx_ky = vector_delta_kx_ky*cmath.exp(-1j*(1+1e-4))计算结果为:
Chern number = (2.0123275393028544+232.56026674927944j)
结果有些许变化。
测试4:某个波函数略微偏离规范,偏离1e-2
vector = vector*cmath.exp(-1j*1)
vector_delta_kx = vector_delta_kx*cmath.exp(-1j*1)
vector_delta_ky = vector_delta_ky*cmath.exp(-1j*1)
vector_delta_kx_ky = vector_delta_kx_ky*cmath.exp(-1j*(1+1e-2))计算结果为:
Chern number = (118.41039702497757+23255.705316755837j)
结果就不正确了。
通过以上的测试可以知道,在数值上只要找到波函数近似的同一规范即可,偏离小量不会影响具体的计算结果。
测试5:某个波函数选取随机规范
rand = np.random.uniform(-pi, pi)
vector_delta_kx_ky = vector_delta_kx_ky*cmath.exp(-1j*rand)计算结果为:
Chern number = (149328.46857940702+12705025.583360218j)
结果不正确。
测试6:二分查找寻找近似的同一规范
某个波函数选取随机规范,然后通过二分查找的方法寻找同一规范。添加的代码如下:
rand = np.random.uniform(-pi, pi)
vector_delta_kx_ky = vector_delta_kx_ky*cmath.exp(-1j*rand)
# 寻找近似的同一的规范
phase_1_pre = 0
phase_2_pre = pi
n_test = 10001
for i0 in range(n_test):
test_1 = np.sum(np.abs(vector_delta_kx_ky*cmath.exp(1j*phase_1_pre) - vector))
test_2 = np.sum(np.abs(vector_delta_kx_ky*cmath.exp(1j*phase_2_pre) - vector))
if test_1 < 1e-6:
phase = phase_1_pre
print('Done with i0=', i0)
break
if i0 == n_test-1:
phase = phase_1_pre
print('Not Found with i0=', i0)
if test_1 < test_2:
if i0 == 0:
phase_1 = phase_1_pre-(phase_2_pre-phase_1_pre)/2
phase_2 = phase_1_pre+(phase_2_pre-phase_1_pre)/2
else:
phase_1 = phase_1_pre
phase_2 = phase_1_pre+(phase_2_pre-phase_1_pre)/2
else:
if i0 == 0:
phase_1 = phase_2_pre-(phase_2_pre-phase_1_pre)/2
phase_2 = phase_2_pre+(phase_2_pre-phase_1_pre)/2
else:
phase_1 = phase_2_pre-(phase_2_pre-phase_1_pre)/2
phase_2 = phase_2_pre
phase_1_pre = phase_1
phase_2_pre = phase_2
vector_delta_kx_ky = vector_delta_kx_ky*cmath.exp(1j*phase)
print('随机的规范=', rand) # 可注释掉
print('二分查找找到的规范=', phase) # 可注释掉
print() # 可注释掉计算结果为:
Done with i0= 22
随机的规范= 0.3549538212139809
二分查找找到的规范= 0.35495326733119054
Done with i0= 23
随机的规范= 0.7747004546374647
二分查找找到的规范= 0.7746999956272478
Done with i0= 23
随机的规范= 1.4110405753724011
二分查找找到的规范= 1.411039867679984
Done with i0= 23
随机的规范= 0.6803154281586488
二分查找找到的规范= 0.6803152363288856
Done with i0= 23
随机的规范= 2.219073275855819
二分查找找到的规范= 2.2190732358674246
Done with i0= 23
随机的规范= 2.959463859887606
二分查找找到的规范= 2.9594631446046926
Done with i0= 23
随机的规范= -1.0637381066354141
二分查找找到的规范= -1.0637385279508642
Chern number = (1.9999999094382561+5.734071432673347j)一个动图例子:
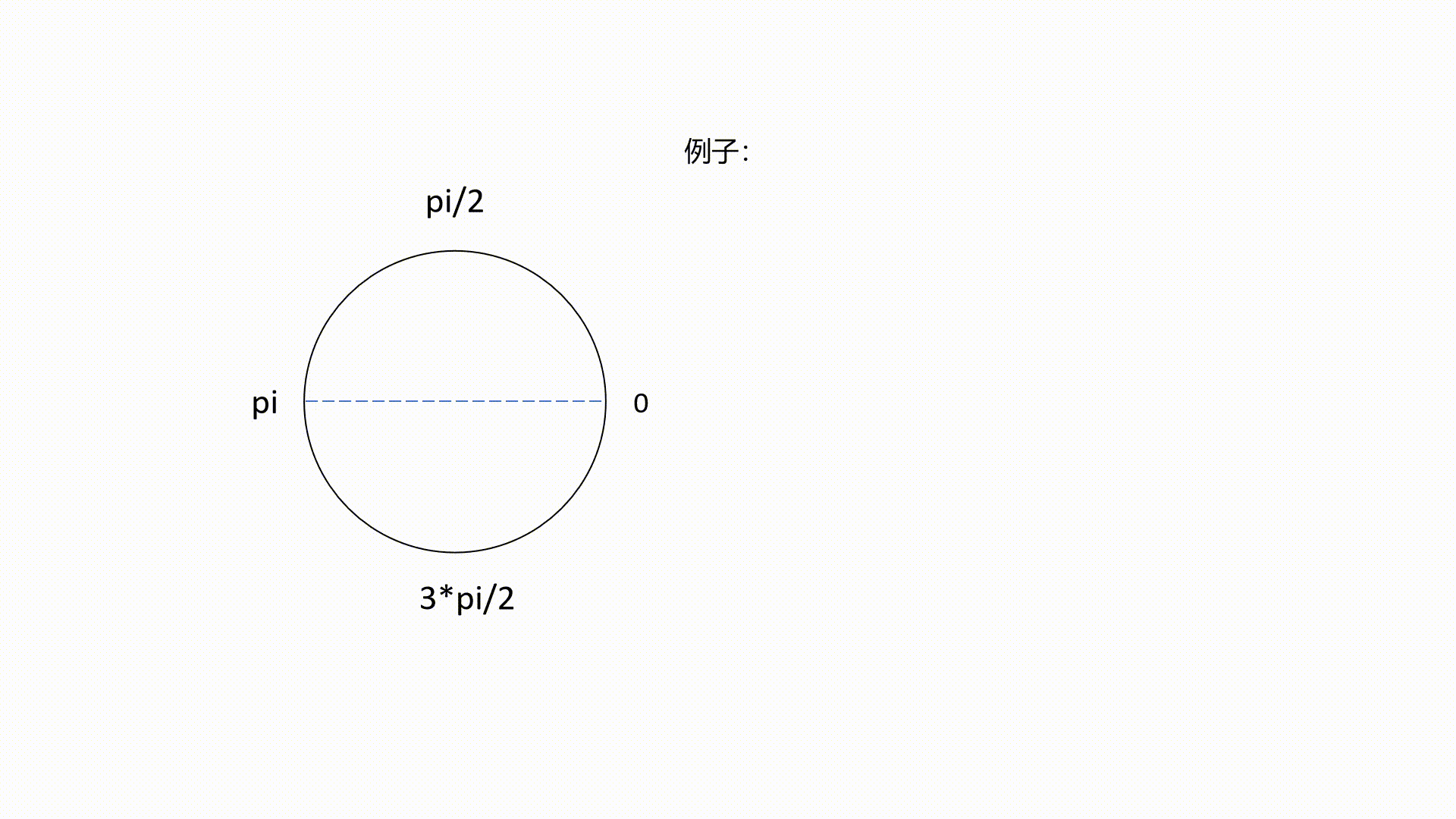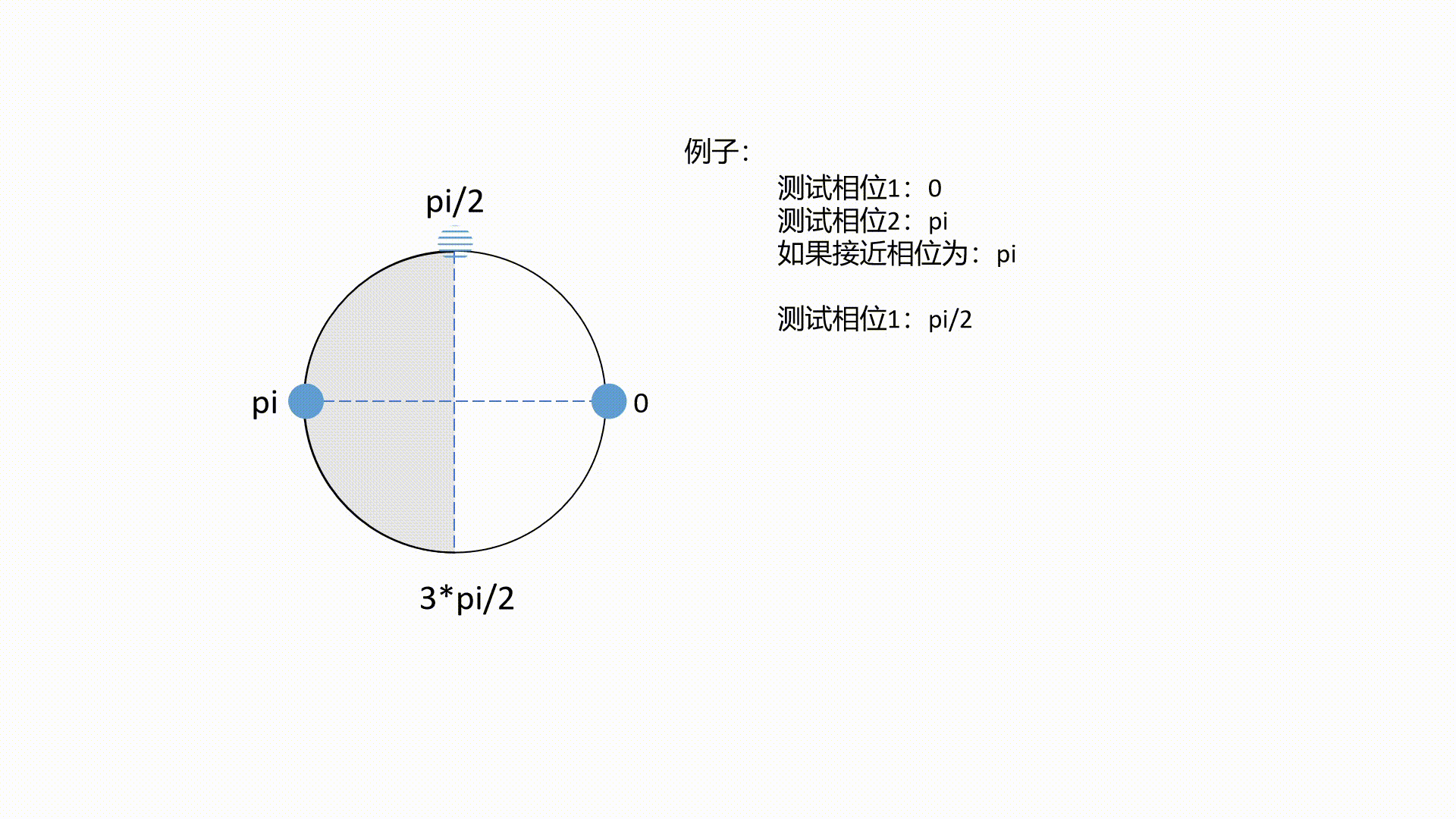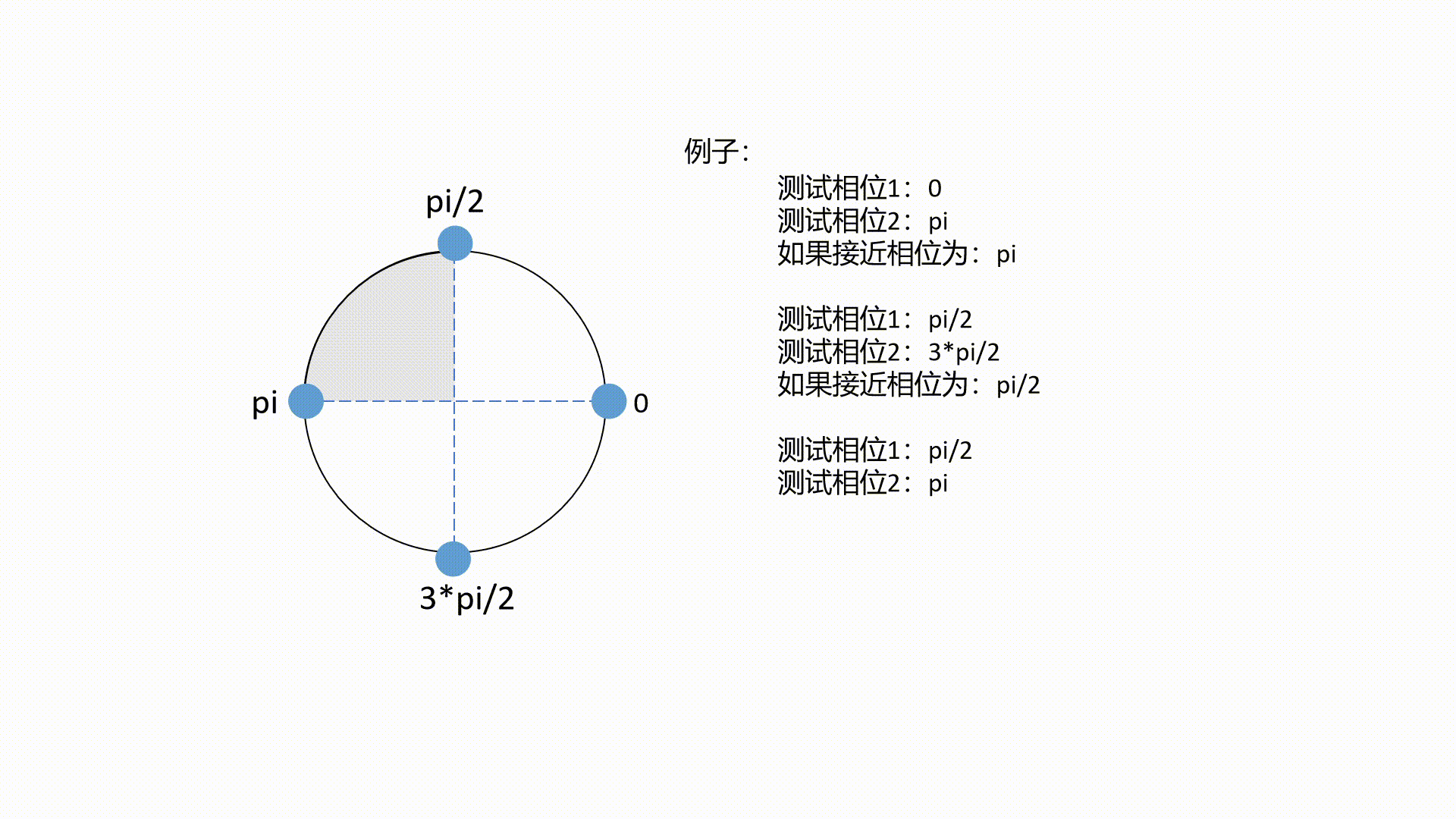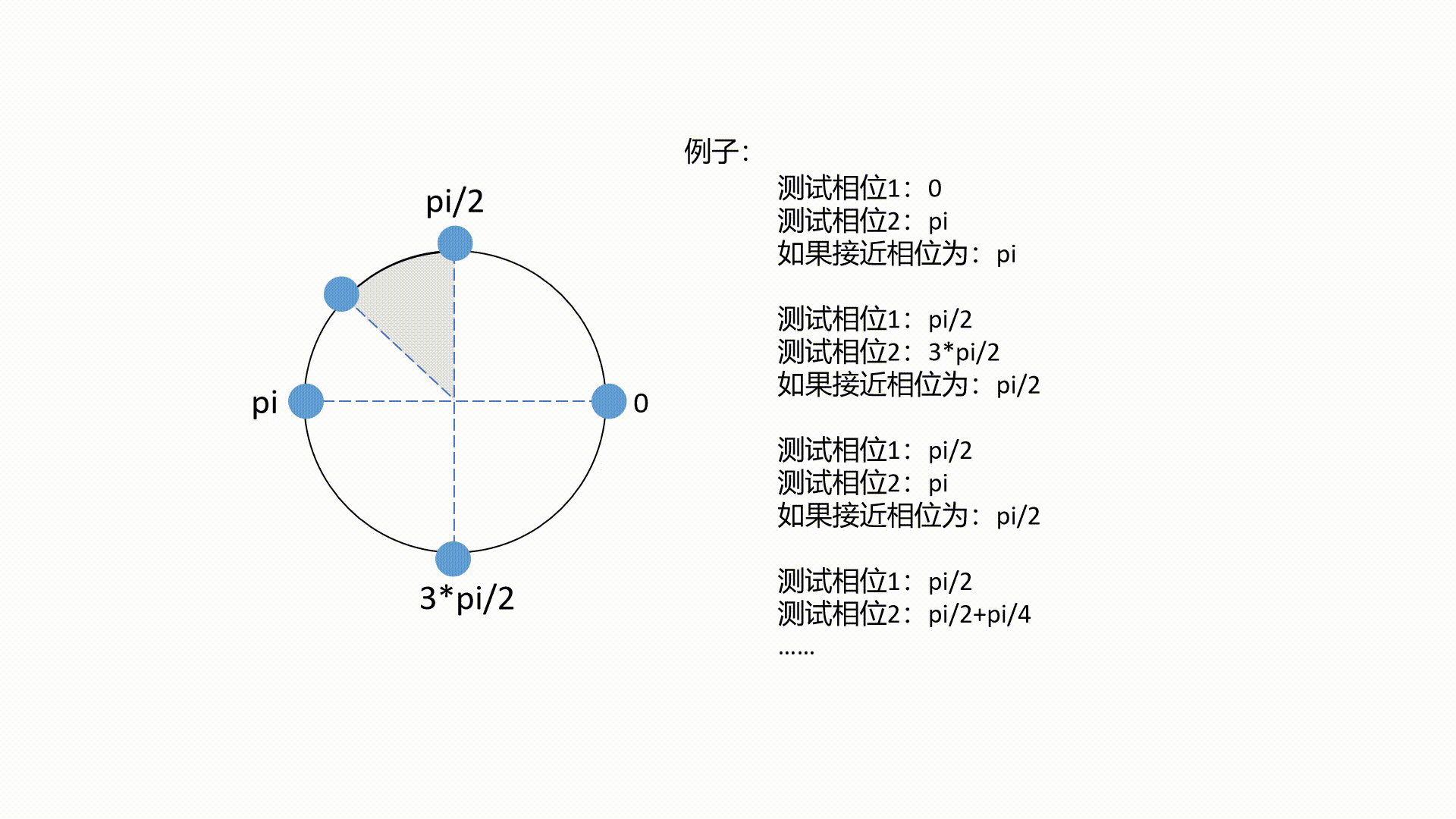
完整的代码如下(可运行的):
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/7516
"""
import numpy as np
from math import * # 引入pi, cos等
import cmath
import time
def hamiltonian(kx, ky): # 量子反常霍尔QAH模型(该参数对应的陈数为2)
t1 = 1.0
t2 = 1.0
t3 = 0.5
m = -1.0
matrix = np.zeros((2, 2))*(1+0j)
matrix[0, 1] = 2*t1*cos(kx)-1j*2*t1*cos(ky)
matrix[1, 0] = 2*t1*cos(kx)+1j*2*t1*cos(ky)
matrix[0, 0] = m+2*t3*sin(kx)+2*t3*sin(ky)+2*t2*cos(kx+ky)
matrix[1, 1] = -(m+2*t3*sin(kx)+2*t3*sin(ky)+2*t2*cos(kx+ky))
return matrix
def main():
start_time = time.time()
n = 100 # 积分密度
delta = 1e-9 # 求导的偏离量
chern_number = 0 # 陈数初始化
for kx in np.arange(-pi, pi, 2*pi/n):
for ky in np.arange(-pi, pi, 2*pi/n):
H = hamiltonian(kx, ky)
eigenvalue, eigenvector = np.linalg.eig(H)
vector = eigenvector[:, np.argsort(np.real(eigenvalue))[0]] # 价带波函数
H_delta_kx = hamiltonian(kx+delta, ky)
eigenvalue, eigenvector = np.linalg.eig(H_delta_kx)
vector_delta_kx = eigenvector[:, np.argsort(np.real(eigenvalue))[0]] # 略偏离kx的波函数
H_delta_ky = hamiltonian(kx, ky+delta)
eigenvalue, eigenvector = np.linalg.eig(H_delta_ky)
vector_delta_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]] # 略偏离ky的波函数
H_delta_kx_ky = hamiltonian(kx+delta, ky+delta)
eigenvalue, eigenvector = np.linalg.eig(H_delta_kx_ky)
vector_delta_kx_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]] # 略偏离kx和ky的波函数
# vector = vector*cmath.exp(-1j*1)
# vector_delta_kx = vector_delta_kx*cmath.exp(-1j*1)
# vector_delta_ky = vector_delta_ky*cmath.exp(-1j*1)
# vector_delta_kx_ky = vector_delta_kx_ky*cmath.exp(-1j*(1+1e-8))
rand = np.random.uniform(-pi, pi)
vector_delta_kx_ky = vector_delta_kx_ky*cmath.exp(-1j*rand)
# 寻找近似的同一的规范
phase_1_pre = 0
phase_2_pre = pi
n_test = 10001
for i0 in range(n_test):
test_1 = np.sum(np.abs(vector_delta_kx_ky*cmath.exp(1j*phase_1_pre) - vector))
test_2 = np.sum(np.abs(vector_delta_kx_ky*cmath.exp(1j*phase_2_pre) - vector))
if test_1 < 1e-6:
phase = phase_1_pre
print('Done with i0=', i0)
break
if i0 == n_test-1:
phase = phase_1_pre
print('Not Found with i0=', i0)
if test_1 < test_2:
if i0 == 0:
phase_1 = phase_1_pre-(phase_2_pre-phase_1_pre)/2
phase_2 = phase_1_pre+(phase_2_pre-phase_1_pre)/2
else:
phase_1 = phase_1_pre
phase_2 = phase_1_pre+(phase_2_pre-phase_1_pre)/2
else:
if i0 == 0:
phase_1 = phase_2_pre-(phase_2_pre-phase_1_pre)/2
phase_2 = phase_2_pre+(phase_2_pre-phase_1_pre)/2
else:
phase_1 = phase_2_pre-(phase_2_pre-phase_1_pre)/2
phase_2 = phase_2_pre
phase_1_pre = phase_1
phase_2_pre = phase_2
vector_delta_kx_ky = vector_delta_kx_ky*cmath.exp(1j*phase)
print('随机的规范=', rand) # 可注释掉
print('二分查找找到的规范=', phase) # 可注释掉
print() # 可注释掉
# 价带的波函数的贝里联络(berry connection) # 求导后内积
A_x = np.dot(vector.transpose().conj(), (vector_delta_kx-vector)/delta) # 贝里联络Ax(x分量)
A_y = np.dot(vector.transpose().conj(), (vector_delta_ky-vector)/delta) # 贝里联络Ay(y分量)
A_x_delta_ky = np.dot(vector_delta_ky.transpose().conj(), (vector_delta_kx_ky-vector_delta_ky)/delta) # 略偏离ky的贝里联络Ax
A_y_delta_kx = np.dot(vector_delta_kx.transpose().conj(), (vector_delta_kx_ky-vector_delta_kx)/delta) # 略偏离kx的贝里联络Ay
# 贝里曲率(berry curvature)
F = (A_y_delta_kx-A_y)/delta-(A_x_delta_ky-A_x)/delta
# 陈数(chern number)
chern_number = chern_number + F*(2*pi/n)**2
chern_number = chern_number/(2*pi*1j)
print('Chern number = ', chern_number)
end_time = time.time()
print('运行时间(min)=', (end_time-start_time)/60)
if __name__ == '__main__':
main()
目前二分法寻找规范的方法已加入开源项目Guan:https://py.guanjihuan.com,使用命令“pip install --upgrade guan”安装到最新版,安装后可直接调用。代码如下:
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/7516
"""
import numpy as np
from math import *
import cmath
import time
import guan
def hamiltonian(kx, ky): # 量子反常霍尔QAH模型(该参数对应的陈数为2)
t1 = 1.0
t2 = 1.0
t3 = 0.5
m = -1.0
matrix = np.zeros((2, 2))*(1+0j)
matrix[0, 1] = 2*t1*cos(kx)-1j*2*t1*cos(ky)
matrix[1, 0] = 2*t1*cos(kx)+1j*2*t1*cos(ky)
matrix[0, 0] = m+2*t3*sin(kx)+2*t3*sin(ky)+2*t2*cos(kx+ky)
matrix[1, 1] = -(m+2*t3*sin(kx)+2*t3*sin(ky)+2*t2*cos(kx+ky))
return matrix
def main():
start_time = time.time()
n = 100 # 积分密度
delta = 1e-9 # 求导的偏离量
chern_number = 0 # 陈数初始化
for kx in np.arange(-pi, pi, 2*pi/n):
for ky in np.arange(-pi, pi, 2*pi/n):
H = hamiltonian(kx, ky)
eigenvalue, eigenvector = np.linalg.eig(H)
vector = eigenvector[:, np.argsort(np.real(eigenvalue))[0]] # 价带波函数
H_delta_kx = hamiltonian(kx+delta, ky)
eigenvalue, eigenvector = np.linalg.eig(H_delta_kx)
vector_delta_kx = eigenvector[:, np.argsort(np.real(eigenvalue))[0]] # 略偏离kx的波函数
H_delta_ky = hamiltonian(kx, ky+delta)
eigenvalue, eigenvector = np.linalg.eig(H_delta_ky)
vector_delta_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]] # 略偏离ky的波函数
H_delta_kx_ky = hamiltonian(kx+delta, ky+delta)
eigenvalue, eigenvector = np.linalg.eig(H_delta_kx_ky)
vector_delta_kx_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]] # 略偏离kx和ky的波函数
# vector = vector*cmath.exp(-1j*1)
# vector_delta_kx = vector_delta_kx*cmath.exp(-1j*1)
# vector_delta_ky = vector_delta_ky*cmath.exp(-1j*1)
# vector_delta_kx_ky = vector_delta_kx_ky*cmath.exp(-1j*(1+1e-8))
rand = np.random.uniform(-pi, pi)
vector_delta_kx_ky = vector_delta_kx_ky*cmath.exp(-1j*rand)
vector_delta_kx_ky = guan.find_vector_with_the_same_gauge_with_binary_search(vector_delta_kx_ky, vector)
# 价带的波函数的贝里联络(berry connection) # 求导后内积
A_x = np.dot(vector.transpose().conj(), (vector_delta_kx-vector)/delta) # 贝里联络Ax(x分量)
A_y = np.dot(vector.transpose().conj(), (vector_delta_ky-vector)/delta) # 贝里联络Ay(y分量)
A_x_delta_ky = np.dot(vector_delta_ky.transpose().conj(), (vector_delta_kx_ky-vector_delta_ky)/delta) # 略偏离ky的贝里联络Ax
A_y_delta_kx = np.dot(vector_delta_kx.transpose().conj(), (vector_delta_kx_ky-vector_delta_kx)/delta) # 略偏离kx的贝里联络Ay
# 贝里曲率(berry curvature)
F = (A_y_delta_kx-A_y)/delta-(A_x_delta_ky-A_x)/delta
# 陈数(chern number)
chern_number = chern_number + F*(2*pi/n)**2
chern_number = chern_number/(2*pi*1j)
print('Chern number = ', chern_number)
end_time = time.time()
print('运行时间(min)=', (end_time-start_time)/60)
if __name__ == '__main__':
main()【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】
老师您好!怎么保证vector_delta_kx_ky*cmath.exp(1j*phase_1_pre) 与 vector总是可以无限接近呢?一些本征向量的不连续点,比如狄拉克点和外耳点,还有一般参数空间上的拓扑突变转变点,在它两侧的两个本征向量没法通过U(1)变换达到相同
你说的这个应该是有简并或交叉的情况,正确做法应该是做幺正变换,处理会稍微复杂些。参考:非简并波函数和简并波函数的固定规范。
关老师您好,请问这个度规具体是怎么选取的呢?test_1 = np.sum(np.abs(vector_delta_kx_ky*cmath.exp(1j*phase_1_pre) - vector))在我看来,这像是要求保证每一个波函数的向量严格与vector相等,这似乎是不可能实现的,请问这该怎么理解呢?
如果k距离无限小,那么每一个波函数向量和相邻的vector相邻的向量近乎于相等,这个就是连续的图像吧。严格来说不是绝对相等,但k间距比较小时,在数值上可以近似这么处理。
感谢大佬的分享,这里有个困惑,我们的目的是为了保证微分时的每一步保持平滑,为什么程序中保证了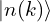 与
与 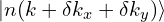 的平滑,但对
的平滑,但对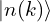 与
与 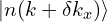 以及
以及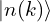 与
与 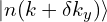 之间没有做规范寻找呢?
之间没有做规范寻找呢?
严格来说,波函数都需要做处理,使其连续,这样求导时才不会发散。在应用中,为了保证结果的正确性,最好都加上。
这里只是因为程序计算出来的波函数恰好就是连续的,所以都不处理结果也没出错。人为地给某个波函数加上一些随机相位,仅仅也是为了测试下算法。
明白了
请问这个1e-6的量是根据什么确定的
极小值,说明该值接近于0。数量级取为1e-4,1e-5,1e-6,1e-7,1e-8都可以。数值上不能太大,也不能太小。
博主,这里加规范是要保证波函数连续,假如我有一个矩形布里渊区,扫略这个布里渊区求本征矢量可以得到一系列波函数,那我是要保证整个布里渊区波函数连续呢还是作一条平行于kx轴或ky轴的线,然后保证这条线上的波函数连续就ok,线与线之间不用连续?
之所以要连续,是因为需要求导。没有求导(差分)的地方就不需要连续,因此基本上是在线上。
matlab版二分查找函数,未验证,py版改写而来:
嗯,用的时候得拿个例子先做下测试。
这个二分法有时候太慢了,而且效果不一定比加负号好。
加负号只是对于特殊情况,不能处理所有的相位。二分法速度还可以,二十几次循环就很接近了。
博主您好,matlab等程序语言产生的附加规范是随机的吗?规范要相同的话是什么时候和什么时候的规范要相同呢?是kx ky都改变一个最小变化量的H和没改变之前的H的特征值的规范要相同吗?
嗯,看程序中调用函数的具体底层算法了,一般来说是随机的,没法给一个特定的规范。
如果要求导,那么需要规范相同,使得波函数连续。
博主您好,为什么波函数要在局限的范围显示连续呢?
如果要对波函数求导的话,那么波函数应该要连续,不然结果会发散。
博主,波函数在数值计算中一般是个列向量,那么所谓的连续是指两个波函数之间每一项的相差都很小吗?这个很小是具体多小呢?如果波函数两两连续,难道真实情况波函数的变化就不会有跳变吗?
嗯,每一项都要很小。相差很小表示的是自身的变化引起的不同,而不是因为规范取的不同而导致的数值上的差别。
真实物理量对规范是不依赖的,比如需要对波函数取模的平方才可以得到概率。