这是之前的一篇：外尔半金属的哈密顿量和费米弧（附Python代码）。本篇计算的是外尔半金属在动量截面上的陈数。
首先把外尔半金属模型的哈密顿量晶格离散化，得到布里渊区的范围在![[-\pi, \pi]](https://www.guanjihuan.com/wp-content/ql-cache/quicklatex.com-c56d4f9cfee295ba5aef7dd7d1bd2c47_l3.png "Rendered by QuickLaTeX.com")
之间。离散的方法参照：常用的泰勒近似，即
离散化后，外尔金属计算能带的代码：
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/6896
"""
import numpy as np
from math import *
import matplotlib.pyplot as plt
def main():
k1 = np.arange(-pi, pi, 0.05)
k2 = np.arange(-pi, pi, 0.05)
plot_bands_two_dimension(k1, k2, hamiltonian)
def hamiltonian(kx,kz,ky=0): # Weyl semimetal
A = 1
M0 = 1
M1 = 1
H = A*(sin(kx)*sigma_x()+sin(ky)*sigma_y())+(M0-M1*(2*(1-cos(kx))+2*(1-cos(ky))+2*(1-cos(kz))))*sigma_z()
return H
def sigma_x():
return np.array([[0, 1],[1, 0]])
def sigma_y():
return np.array([[0, -1j],[1j, 0]])
def sigma_z():
return np.array([[1, 0],[0, -1]])
def plot_bands_two_dimension(k1, k2, hamiltonian):
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
from matplotlib.ticker import LinearLocator, FormatStrFormatter
dim = hamiltonian(0, 0).shape[0]
dim1 = k1.shape[0]
dim2 = k2.shape[0]
eigenvalue_k = np.zeros((dim2, dim1, dim))
i0 = 0
for k10 in k1:
j0 = 0
for k20 in k2:
matrix0 = hamiltonian(k10, k20)
eigenvalue, eigenvector = np.linalg.eig(matrix0)
eigenvalue_k[j0, i0, :] = np.sort(np.real(eigenvalue[:]))
j0 += 1
i0 += 1
fig = plt.figure()
ax = fig.gca(projection='3d')
k1, k2 = np.meshgrid(k1, k2)
for dim0 in range(dim):
ax.plot_surface(k1, k2, eigenvalue_k[:, :, dim0], cmap=cm.coolwarm, linewidth=0, antialiased=False)
plt.xlabel('kx')
plt.ylabel('kz')
ax.set_zlabel('E')
plt.show()
if __name__ == '__main__':
main()计算结果为：
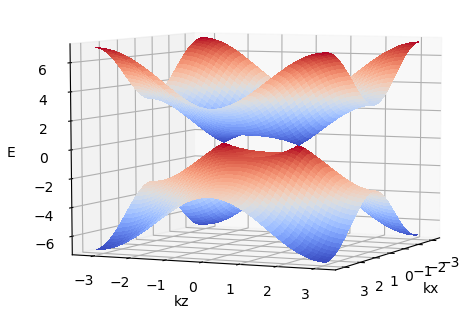
把离散化的哈密顿量和之前的这篇代码相结合：陈数Chern number的计算（高效法，附Python/Matlab代码），得到：
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/6896
"""
import numpy as np
from math import *
import matplotlib.pyplot as plt
import time
import cmath
def hamiltonian(kx,ky,kz): # Weyl semimetal
A = 1
M0 = 1
M1 = 1
H = A*(sin(kx)*sigma_x()+sin(ky)*sigma_y())+(M0-M1*(2*(1-cos(kx))+2*(1-cos(ky))+2*(1-cos(kz))))*sigma_z()
return H
def sigma_x():
return np.array([[0, 1],[1, 0]])
def sigma_y():
return np.array([[0, -1j],[1j, 0]])
def sigma_z():
return np.array([[1, 0],[0, -1]])
def main():
start_time = time.time()
n = 50
delta = 2*pi/n
kz_array = np.arange(-pi, pi, 0.1)
chern_number_array = np.zeros(kz_array.shape[0])
i0 = 0
for kz in kz_array:
print('kz=', kz)
chern_number = 0 # 陈数初始化
for kx in np.arange(-pi, pi, 2*pi/n):
for ky in np.arange(-pi, pi, 2*pi/n):
H = hamiltonian(kx, ky, kz)
eigenvalue, eigenvector = np.linalg.eig(H)
vector = eigenvector[:, np.argsort(np.real(eigenvalue))[0]] # 价带波函数
H_delta_kx = hamiltonian(kx+delta, ky, kz)
eigenvalue, eigenvector = np.linalg.eig(H_delta_kx)
vector_delta_kx = eigenvector[:, np.argsort(np.real(eigenvalue))[0]] # 略偏离kx的波函数
H_delta_ky = hamiltonian(kx, ky+delta, kz)
eigenvalue, eigenvector = np.linalg.eig(H_delta_ky)
vector_delta_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]] # 略偏离ky的波函数
H_delta_kx_ky = hamiltonian(kx+delta, ky+delta, kz)
eigenvalue, eigenvector = np.linalg.eig(H_delta_kx_ky)
vector_delta_kx_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]] # 略偏离kx和ky的波函数
Ux = np.dot(np.conj(vector), vector_delta_kx)/abs(np.dot(np.conj(vector), vector_delta_kx))
Uy = np.dot(np.conj(vector), vector_delta_ky)/abs(np.dot(np.conj(vector), vector_delta_ky))
Ux_y = np.dot(np.conj(vector_delta_ky), vector_delta_kx_ky)/abs(np.dot(np.conj(vector_delta_ky), vector_delta_kx_ky))
Uy_x = np.dot(np.conj(vector_delta_kx), vector_delta_kx_ky)/abs(np.dot(np.conj(vector_delta_kx), vector_delta_kx_ky))
F = cmath.log(Ux*Uy_x*(1/Ux_y)*(1/Uy))
# 陈数(chern number)
chern_number = chern_number + F
chern_number = chern_number/(2*pi*1j)
print('Chern number = ', chern_number, '\n')
chern_number_array[i0] = np.real(chern_number)
i0 += 1
end_time = time.time()
print('运行时间(min)=', (end_time-start_time)/60)
plt.plot(kz_array, chern_number_array, 'o-')
plt.xlabel('kz')
plt.ylabel('Chern number')
plt.show()
if __name__ == '__main__':
main()计算结果为：
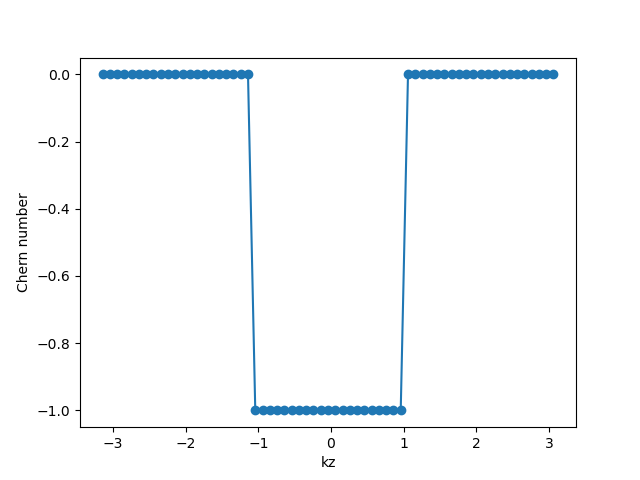
可以看出：在两个外尔点之间的动量截面上，陈数不为零。
使用Guan开源软件包（https://py.guanjihuan.com），代码如下：
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/6896
"""
import numpy as np
import guan
import functools
def main():
kz_array = np.arange(-np.pi, np.pi, 0.1)
chern_number_array = []
for kz in kz_array:
print(kz)
hamiltonian_function = functools.partial(hamiltonian, kz=kz)
chern_number = guan.calculate_chern_number_for_square_lattice_with_efficient_method(hamiltonian_function)
chern_number_array.append(chern_number)
guan.plot(kz_array, chern_number_array, style='-o')
def hamiltonian(kx,ky,kz): # Weyl semimetal
A = 1
M0 = 1
M1 = 1
H = A*(np.sin(kx)*guan.sigma_x()+np.sin(ky)*guan.sigma_y())+(M0-M1*(2*(1-np.cos(kx))+2*(1-np.cos(ky))+2*(1-np.cos(kz))))*guan.sigma_z()
return H
if __name__ == '__main__':
main()
【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】
想看看博主出一期强关联计算的文章
谢谢你的建议。我对这方面还不是很了解，接触的不多，之后如果有学习到，可能会写。
博主，我看到你今年文章里面有计算Loop Polarization，可以出一篇相关的文章嘛
我也想过，一直没写，哈哈。谢谢提醒。已更博：在霍普夫半金属中的圈极化现象（Loop Polarization in Hopf Semimetals）。主要介绍那边文章的内容。有什么问题随时可以联系。
赞赞赞，谢谢博主！
嗯嗯