多端体系的量子输运（附Python代码）

这是之前的一篇博文，计算的是两端体系的量子输运：非平衡格林函数计算电导（附Python代码）。这里计算六端口体系的量子输运，以方格子为例，给出三份代码：

第一个写出全部算法的代码。
第二个调用了Guan开源软件包（https://py.guanjihuan.com）。
第三个用Kwant进行计算（https://www.kwant-project.org/）。

一、代码1

说明：这里只是一个测试例子。在实际计算中，需要把四个电极往中间移一点，即move>0，否则相邻电极会相互接触，达不到预期结果。

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/6075
"""

import numpy as np
import matplotlib.pyplot as plt
import copy
import time


def get_lead_h00(width):  
    h00 = np.zeros((width, width))
    for i0 in range(width-1):
        h00[i0, i0+1] = 1
        h00[i0+1, i0] = 1
    return h00


def get_lead_h01(width):
    h01 = np.identity(width)
    return h01


def get_center_hamiltonian(Nx, Ny):
    h = np.zeros((Nx*Ny, Nx*Ny))
    for x0 in range(Nx-1):
        for y0 in range(Ny):
            h[x0*Ny+y0, (x0+1)*Ny+y0] = 1 # x方向的跃迁
            h[(x0+1)*Ny+y0, x0*Ny+y0] = 1
    for x0 in range(Nx):
        for y0 in range(Ny-1):
            h[x0*Ny+y0, x0*Ny+y0+1] = 1 # y方向的跃迁
            h[x0*Ny+y0+1, x0*Ny+y0] = 1 
    return h


def main():
    start_time = time.time()
    width = 5
    length = 50 
    fermi_energy_array = np.arange(-4, 4, .01)

    # 中心区的哈密顿量
    H_center = get_center_hamiltonian(Nx=length, Ny=width)

    # 电极的h00和h01
    lead_h00 = get_lead_h00(width)
    lead_h01 = get_lead_h01(width)
    
    transmission_12_array = []
    transmission_13_array = []
    transmission_14_array = []
    transmission_15_array = []
    transmission_16_array = []
    transmission_1_all_array = []

    for fermi_energy in fermi_energy_array:
        print(fermi_energy)
        # 表面格林函数
        right_lead_surface, left_lead_surface = surface_green_function_lead(fermi_energy + 1e-9j, lead_h00, lead_h01, dim=width)

        # 由于镜面对称以及xy各项同性，因此这里六个电极的表面格林函数具有相同的形式
        lead_1 = copy.deepcopy(right_lead_surface)  # 镜面对称使得lead_1=lead_4
        lead_2 = copy.deepcopy(right_lead_surface)  # xy各向同性使得lead_2=lead_4
        lead_3 = copy.deepcopy(right_lead_surface)
        lead_4 = copy.deepcopy(right_lead_surface)  
        lead_5 = copy.deepcopy(right_lead_surface)
        lead_6 = copy.deepcopy(right_lead_surface)

        #   几何形状如下所示：
        #               lead2         lead3
        #   lead1(L)                          lead4(R)  
        #               lead6         lead5 

        # 电极到中心区的跃迁矩阵
        H_lead_1_to_center = np.zeros((width, width*length), dtype=complex)
        H_lead_2_to_center = np.zeros((width, width*length), dtype=complex)
        H_lead_3_to_center = np.zeros((width, width*length), dtype=complex)
        H_lead_4_to_center = np.zeros((width, width*length), dtype=complex)
        H_lead_5_to_center = np.zeros((width, width*length), dtype=complex)
        H_lead_6_to_center = np.zeros((width, width*length), dtype=complex)
        move = 0 # the step of leads 2,3,6,5 moving to center
        for i0 in range(width):
            H_lead_1_to_center[i0, i0] = 1
            H_lead_2_to_center[i0, width*(move+i0)+(width-1)] = 1
            H_lead_3_to_center[i0, width*(length-move-1-i0)+(width-1)] = 1
            H_lead_4_to_center[i0, width*(length-1)+i0] = 1
            H_lead_5_to_center[i0, width*(length-move-1-i0)+0] = 1
            H_lead_6_to_center[i0, width*(move+i0)+0] = 1

        # 自能    
        self_energy_1 = np.dot(np.dot(H_lead_1_to_center.transpose().conj(), lead_1), H_lead_1_to_center)
        self_energy_2 = np.dot(np.dot(H_lead_2_to_center.transpose().conj(), lead_2), H_lead_2_to_center)
        self_energy_3 = np.dot(np.dot(H_lead_3_to_center.transpose().conj(), lead_3), H_lead_3_to_center)
        self_energy_4 = np.dot(np.dot(H_lead_4_to_center.transpose().conj(), lead_4), H_lead_4_to_center)
        self_energy_5 = np.dot(np.dot(H_lead_5_to_center.transpose().conj(), lead_5), H_lead_5_to_center)
        self_energy_6 = np.dot(np.dot(H_lead_6_to_center.transpose().conj(), lead_6), H_lead_6_to_center)

        # 整体格林函数
        green = np.linalg.inv(fermi_energy*np.eye(width*length)-H_center-self_energy_1-self_energy_2-self_energy_3-self_energy_4-self_energy_5-self_energy_6)

        # Gamma矩阵
        gamma_1 = 1j*(self_energy_1-self_energy_1.transpose().conj())
        gamma_2 = 1j*(self_energy_2-self_energy_2.transpose().conj())
        gamma_3 = 1j*(self_energy_3-self_energy_3.transpose().conj())
        gamma_4 = 1j*(self_energy_4-self_energy_4.transpose().conj())
        gamma_5 = 1j*(self_energy_5-self_energy_5.transpose().conj())
        gamma_6 = 1j*(self_energy_6-self_energy_6.transpose().conj())

        # Transmission
        transmission_12 = np.trace(np.dot(np.dot(np.dot(gamma_1, green), gamma_2), green.transpose().conj()))
        transmission_13 = np.trace(np.dot(np.dot(np.dot(gamma_1, green), gamma_3), green.transpose().conj()))
        transmission_14 = np.trace(np.dot(np.dot(np.dot(gamma_1, green), gamma_4), green.transpose().conj()))
        transmission_15 = np.trace(np.dot(np.dot(np.dot(gamma_1, green), gamma_5), green.transpose().conj()))
        transmission_16 = np.trace(np.dot(np.dot(np.dot(gamma_1, green), gamma_6), green.transpose().conj()))

        transmission_12_array.append(np.real(transmission_12))
        transmission_13_array.append(np.real(transmission_13))
        transmission_14_array.append(np.real(transmission_14))
        transmission_15_array.append(np.real(transmission_15))
        transmission_16_array.append(np.real(transmission_16))
        transmission_1_all_array.append(np.real(transmission_12+transmission_13+transmission_14+transmission_15+transmission_16))
    
    Plot_Line(fermi_energy_array, transmission_12_array, xlabel='Fermi energy', ylabel='Transmission_12', title='', filename='a')
    Plot_Line(fermi_energy_array, transmission_13_array, xlabel='Fermi energy', ylabel='Transmission_13', title='', filename='a')
    Plot_Line(fermi_energy_array, transmission_14_array, xlabel='Fermi energy', ylabel='Transmission_14', title='', filename='a')
    Plot_Line(fermi_energy_array, transmission_15_array, xlabel='Fermi energy', ylabel='Transmission_15', title='', filename='a')
    Plot_Line(fermi_energy_array, transmission_16_array, xlabel='Fermi energy', ylabel='Transmission_16', title='', filename='a')
    Plot_Line(fermi_energy_array, transmission_1_all_array, xlabel='Fermi energy', ylabel='Transmission_1_all', title='', filename='a')
    end_time = time.time()
    print('运行时间=', end_time-start_time)



def Plot_Line(x, y, xlabel='x', ylabel='y', title='', filename='a'): 
    import matplotlib.pyplot as plt
    fig, ax = plt.subplots()
    plt.subplots_adjust(bottom=0.20, left=0.18) 
    ax.plot(x, y, '-')
    ax.grid()
    ax.set_title(title, fontsize=20, fontfamily='Times New Roman')
    ax.set_xlabel(xlabel, fontsize=20, fontfamily='Times New Roman') 
    ax.set_ylabel(ylabel, fontsize=20, fontfamily='Times New Roman') 
    ax.tick_params(labelsize=20) 
    labels = ax.get_xticklabels() + ax.get_yticklabels()
    [label.set_fontname('Times New Roman') for label in labels]  
    # plt.savefig(filename+'.jpg', dpi=300) 
    plt.show()
    plt.close('all')

def transfer_matrix(fermi_energy, h00, h01, dim):   # 转移矩阵T
    transfer = np.zeros((2*dim, 2*dim))*(0+0j)  
    transfer[0:dim, 0:dim] = np.dot(np.linalg.inv(h01), fermi_energy*np.identity(dim)-h00)  
    transfer[0:dim, dim:2*dim] = np.dot(-1*np.linalg.inv(h01), h01.transpose().conj())
    transfer[dim:2*dim, 0:dim] = np.identity(dim)
    transfer[dim:2*dim, dim:2*dim] = 0 
    return transfer  # 返回转移矩阵


def surface_green_function_lead(fermi_energy, h00, h01, dim):  # 电极的表面格林函数
    transfer = transfer_matrix(fermi_energy, h00, h01, dim)
    eigenvalue, eigenvector = np.linalg.eig(transfer)
    ind = np.argsort(np.abs(eigenvalue))
    temp = np.zeros((2*dim, 2*dim))*(1+0j)
    i0 = 0
    for ind0 in ind:
        temp[:, i0] = eigenvector[:, ind0]
        i0 += 1
    s1 = temp[dim:2*dim, 0:dim]
    s2 = temp[0:dim, 0:dim]
    s3 = temp[dim:2*dim, dim:2*dim]
    s4 = temp[0:dim, dim:2*dim]
    right_lead_surface = np.linalg.inv(fermi_energy*np.identity(dim)-h00-np.dot(np.dot(h01, s2), np.linalg.inv(s1)))
    left_lead_surface = np.linalg.inv(fermi_energy*np.identity(dim)-h00-np.dot(np.dot(h01.transpose().conj(), s3), np.linalg.inv(s4)))
    return right_lead_surface, left_lead_surface  # 返回右电极的表面格林函数和左电极的表面格林函数


if __name__ == '__main__':
    main()

计算结果为：

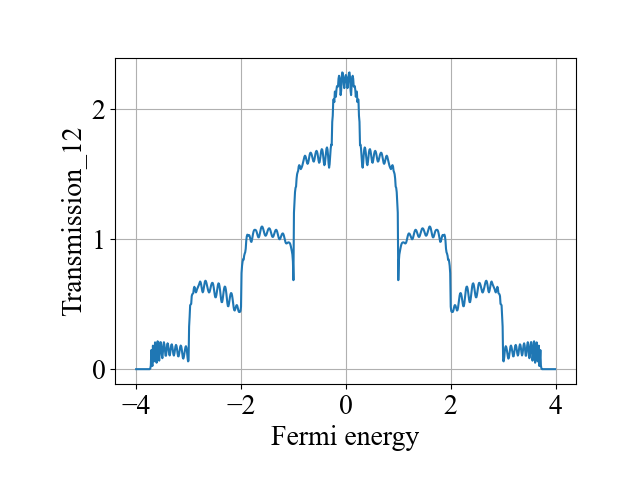
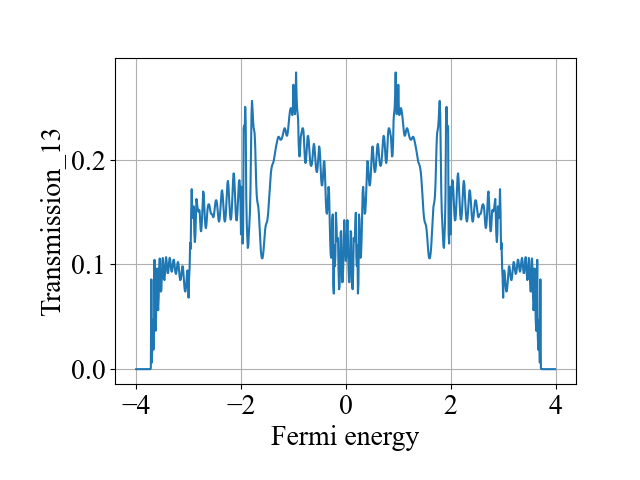
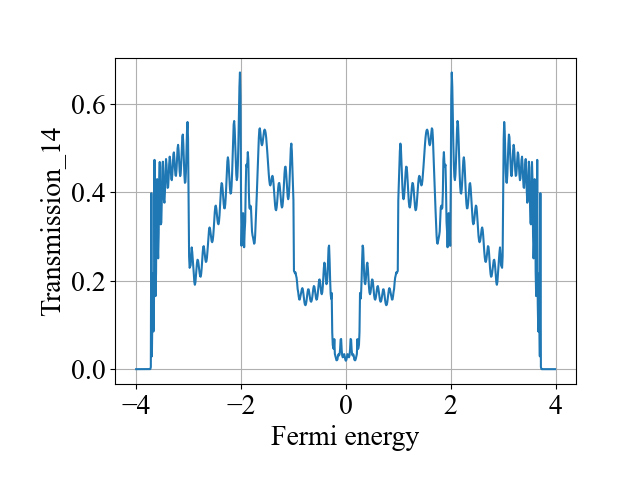
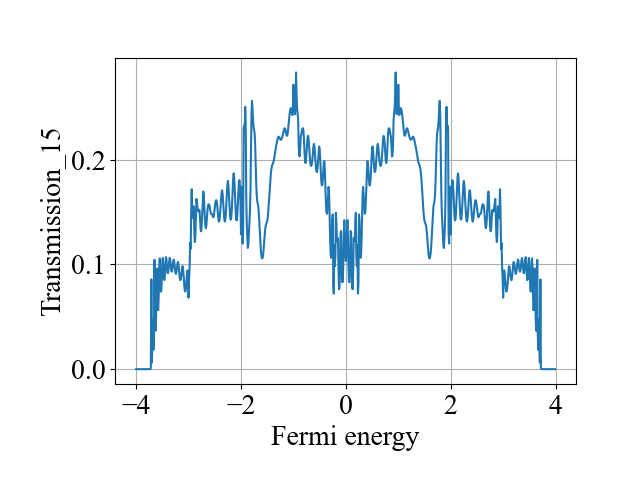
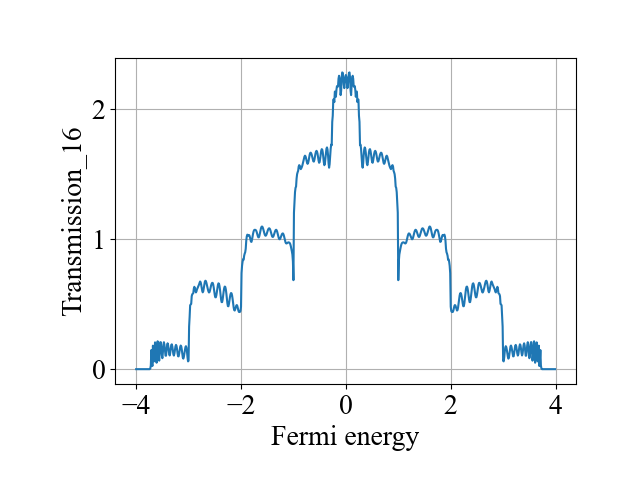
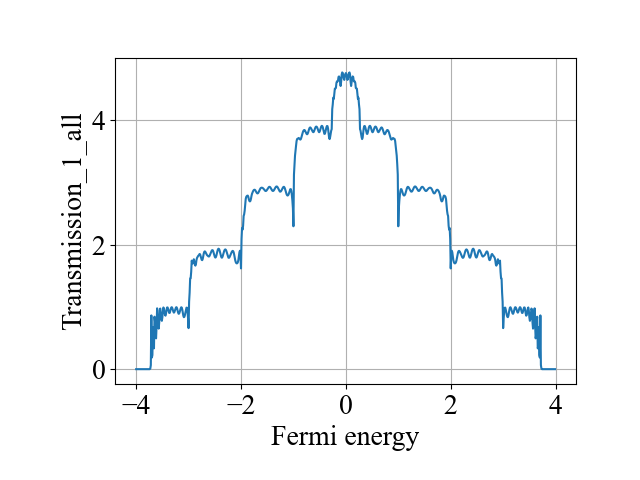
二、代码2

如果用Guan开源软件包：https://py.guanjihuan.com，可省去部分代码，程序会更简洁一些，代码如下：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/6075
"""

import numpy as np
import time
import guan

def get_lead_h00(width):  
    h00 = np.zeros((width, width))
    for i0 in range(width-1):
        h00[i0, i0+1] = 1
        h00[i0+1, i0] = 1
    return h00


def get_lead_h01(width):
    h01 = np.identity(width)
    return h01


def get_center_hamiltonian(Nx, Ny):
    h = np.zeros((Nx*Ny, Nx*Ny))
    for x0 in range(Nx-1):
        for y0 in range(Ny):
            h[x0*Ny+y0, (x0+1)*Ny+y0] = 1 # x方向的跃迁
            h[(x0+1)*Ny+y0, x0*Ny+y0] = 1
    for x0 in range(Nx):
        for y0 in range(Ny-1):
            h[x0*Ny+y0, x0*Ny+y0+1] = 1 # y方向的跃迁
            h[x0*Ny+y0+1, x0*Ny+y0] = 1 
    return h


def main():
    start_time = time.time()
    width = 5
    length = 50 
    fermi_energy_array = np.arange(-4, 4, .01)
    # 中心区的哈密顿量
    center_hamiltonian = get_center_hamiltonian(Nx=length, Ny=width)
    # 电极的h00和h01
    lead_h00 = get_lead_h00(width)
    lead_h01 = get_lead_h01(width)
    transmission_12_array = []
    transmission_13_array = []
    transmission_14_array = []
    transmission_15_array = []
    transmission_16_array = []
    transmission_1_all_array = []
    for fermi_energy in fermi_energy_array:
        print(fermi_energy)
        #   几何形状如下所示：
        #               lead2         lead3
        #   lead1(L)                          lead4(R)  
        #               lead6         lead5 

        transmission_12, transmission_13, transmission_14, transmission_15, transmission_16 = guan.calculate_six_terminal_transmissions_from_lead_1(fermi_energy, h00_for_lead_4=lead_h00, h01_for_lead_4=lead_h01, h00_for_lead_2=lead_h00, h01_for_lead_2=lead_h01, center_hamiltonian=center_hamiltonian, width=width, length=length, internal_degree=1, moving_step_of_leads=0)
        transmission_12_array.append(transmission_12)
        transmission_13_array.append(transmission_13)
        transmission_14_array.append(transmission_14)
        transmission_15_array.append(transmission_15)
        transmission_16_array.append(transmission_16)
        transmission_1_all_array.append(\
            transmission_12+transmission_13+transmission_14+transmission_15+transmission_16)

        # transmission_matrix = guan.calculate_six_terminal_transmission_matrix(fermi_energy, h00_for_lead_4=lead_h00, h01_for_lead_4=lead_h01, h00_for_lead_2=lead_h00, h01_for_lead_2=lead_h01, center_hamiltonian=center_hamiltonian, width=width, length=length, internal_degree=1, moving_step_of_leads=0)
        # transmission_12_array.append(transmission_matrix[0, 1])
        # transmission_13_array.append(transmission_matrix[0, 2])
        # transmission_14_array.append(transmission_matrix[0, 3])
        # transmission_15_array.append(transmission_matrix[0, 4])
        # transmission_16_array.append(transmission_matrix[0, 5])
        # transmission_1_all_array.append(transmission_matrix[0, 1]+transmission_matrix[0, 2]+transmission_matrix[0, 3]+transmission_matrix[0, 4]+transmission_matrix[0, 5])

    guan.plot(fermi_energy_array, transmission_12_array, xlabel='Fermi energy', ylabel='Transmission_12')
    guan.plot(fermi_energy_array, transmission_13_array, xlabel='Fermi energy', ylabel='Transmission_13')
    guan.plot(fermi_energy_array, transmission_14_array, xlabel='Fermi energy', ylabel='Transmission_14')
    guan.plot(fermi_energy_array, transmission_15_array, xlabel='Fermi energy', ylabel='Transmission_15')
    guan.plot(fermi_energy_array, transmission_16_array, xlabel='Fermi energy', ylabel='Transmission_16')
    guan.plot(fermi_energy_array, transmission_1_all_array, xlabel='Fermi energy', ylabel='Transmission_1_all')
    end_time = time.time()
    print('运行时间（分）=', (end_time-start_time)/60)


if __name__ == '__main__':
    main()

三、代码3

使用Kwant来计算：https://www.kwant-project.org/，代码如下：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/6075
"""

import kwant
import numpy as np
from matplotlib import pyplot

def make_system():
    a = 1
    lat = kwant.lattice.square(a)
    syst = kwant.Builder()
    t = 1.0
    W = 5
    L = 50
    syst[(lat(x, y) for x in range(L) for y in range(W))] = 0
    syst[lat.neighbors()] = -t  
    #   几何形状如下所示：
    #               lead2         lead3
    #   lead1(L)                          lead4(R)  
    #               lead6         lead5

    move = 0 # the step of leads 2,3,6,5 moving to center

    lead1 = kwant.Builder(kwant.TranslationalSymmetry((-a, 0)))
    lead1[(lat(0, j) for j in range(W))] = 0
    lead1[lat.neighbors()] = -t
    syst.attach_lead(lead1) 

    lead2 = kwant.Builder(kwant.TranslationalSymmetry((0, -a)))
    lead2[(lat(move+j, 0) for j in range(W))] = 0
    lead2[lat.neighbors()] = -t  
    syst.attach_lead(lead2) 

    lead3 = kwant.Builder(kwant.TranslationalSymmetry((0, -a)))
    lead3[(lat(j+(L-W-move), 0) for j in range(W))] = 0
    lead3[lat.neighbors()] = -t  
    syst.attach_lead(lead3) 

    syst.attach_lead(lead1.reversed())   # lead4
    syst.attach_lead(lead3.reversed())   # lead5
    syst.attach_lead(lead2.reversed())   # lead6

    kwant.plot(syst) 
    syst = syst.finalized() 
    return syst


def main():
    syst = make_system()
    energies = np.linspace(-4, 4, 800)
    data1 = []
    data2 = []
    data3 = []
    data4 = []
    data5 = []
    data6 = []
    for energy in energies:
        smatrix = kwant.smatrix(syst, energy)  
        data1.append(smatrix.transmission(1, 0))   # compute the transmission probability from lead 0 to lead 1
        data2.append(smatrix.transmission(2, 0))
        data3.append(smatrix.transmission(3, 0))
        data4.append(smatrix.transmission(4, 0))
        data5.append(smatrix.transmission(5, 0))
        data6.append(smatrix.transmission(1, 0)+smatrix.transmission(2, 0)+smatrix.transmission(3, 0)+smatrix.transmission(4, 0)+smatrix.transmission(5, 0))
    pyplot.plot(energies, data1)
    pyplot.xlabel("energy [t]")
    pyplot.ylabel("Transmission_12 [e^2/h]")
    pyplot.show()
    pyplot.plot(energies, data2)
    pyplot.xlabel("energy [t]")
    pyplot.ylabel("Transmission_13 [e^2/h]")
    pyplot.show()
    pyplot.plot(energies, data3)
    pyplot.xlabel("energy [t]")
    pyplot.ylabel("Transmission_14 [e^2/h]")
    pyplot.show()
    pyplot.plot(energies, data4)
    pyplot.xlabel("energy [t]")
    pyplot.ylabel("Transmission_15 [e^2/h]")
    pyplot.show()
    pyplot.plot(energies, data5)
    pyplot.xlabel("energy [t]")
    pyplot.ylabel("Transmission_16 [e^2/h]")
    pyplot.show()
    pyplot.plot(energies, data6)
    pyplot.xlabel("energy [t]")
    pyplot.ylabel("Transmission_1_all [e^2/h]")
    pyplot.show()


if __name__ == '__main__':
    main()

当move=0时，运行结果：

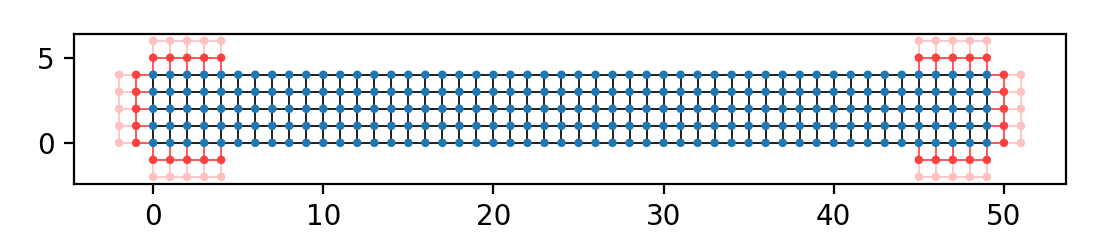
计算得到的透射率和以上程序的结果相同。

当move=5时，运行结果：

3,730 次浏览

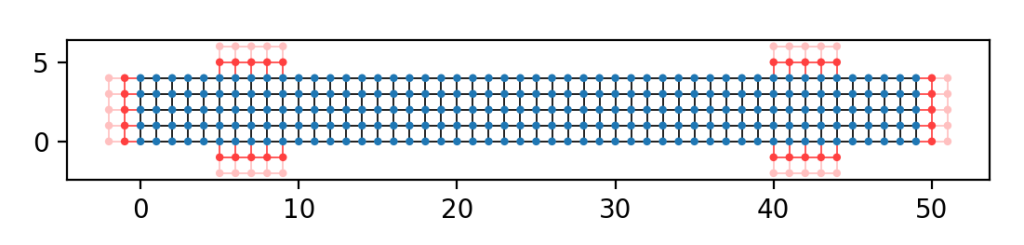
【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】

25 thoughts on “多端体系的量子输运（附Python代码）”

匿名说道：

2024年11月21日 15:13

作者您好！我再计算陈绝缘体的六端口体系的时候自能是用Sigma=h10*gr*h01来计算的，在Ef接近0的时候霍尔电阻突然发散，我检查了数据发现Ef接近0时Gamma函数也接近0，但在Ef取其他的值时都正常，想请教您一下这是由什么原因产生的。（ps：我是用matlab来计算的霍尔电阻）

回复
1. guanjihuan说道：
  
  2024年11月22日 08:22
  
  这个问题应该不是bug，是正常数值计算现象。可能的原因是这个地方能带是平的或者有交叉点，可能的解决方法是可以把虚部的小量增大一些，或者哈密顿量上加上极小的对角项，或者直接不考虑E=0的值，只考虑零附近的值。
  
  回复
  1. 匿名说道：
    
    2024年11月22日 10:09
    
    我画了一下能带，发现霍尔电阻发散时，Ef正处于带隙之中，正常情况应该是当Ef在gap中时，Rxy=1。
    
    回复
    1. guanjihuan说道：
      
      2024年11月25日 02:10
      
      哦哦，那可能不是物理上的结果，只是数值的上的错误。我也不清楚是什么原因，这有可能是当E=0时，某个矩阵求逆或者其他运算时发散了。解决方法可以考虑上面说的，或者直接不考虑这个导致错误的特殊的值。
      
      回复
      1. 匿名说道：
        
        2024年11月26日 15:14
        
        好的，感谢指导！
        
        回复
匿名说道：

2024年8月2日 18:17

感谢作者大大！还有一个问题就是我在这个模型中外加了磁场，参考了您写的方格子的霍夫斯塔特蝴蝶这篇文章，在跳跃能加上了相位因子，然后跑出来的图像还是和不加磁场的是一样的，请问这种情况是对的吗？而且加上磁场后T12=T21,有相位的改变，对称被破坏还会出现这种情况吗？

回复
1. guanjihuan说道：
  
  2024年8月2日 19:21
  
  加了磁场，有朗道能级和对应的边缘态，结果应该是相邻的电极之间有传输，可以参考：介观体系中的Landauer–Büttiker公式、方格子紧束缚模型中朗道能级的陈数/霍尔电导（附Python代码）。
  
  回复
  1. 匿名说道：
    
    2024年8月3日 20:06
    
    十分感谢！！！！！！！
    
    回复
匿名说道：

2024年7月29日 15:13

作者您好！请问一下这个透射系数T是可能大于1的嘛？因为在您的结果中T12已经到达2了。

回复
1. guanjihuan说道：
  
  2024年7月29日 21:56
  
  一个电极中有多个通道模式，例如，这里宽度取为5，能带在费米能为零的位置有5个通道模式，因此T_{1->other leads}之和最高可以达到5，如果包括了反射系数，那么值就是5。
  
  回复
  1. 匿名说道：
    
    2024年8月28日 18:26
    
    作者您好，我想问一下如果只链接一个通道是需要修改电极这个部分吗？怎么修改呀？
    def get_lead_h00(width):
    h00 = np.zeros((width, width))
    for i0 in range(width-1):
    h00[i0, i0+1] = 1
    h00[i0+1, i0] = 1
    return h00
    def get_lead_h01(width):
    h01 = np.identity(width)
    return h01
    
    回复
    1. guanjihuan说道：
      
      2024年8月28日 19:07
      
      如果只是修改电极的通道数，那么把电极的 width 取为1，而中心区的 width 为其他值。这时候主要修改 H_lead_1_to_center 这个电极和中心区的耦合矩阵。
      
      回复
匿名说道：

2021年12月24日 13:16

博主你好，为什么transmission fuction 有震荡呢？

回复
1. guanjihuan说道：
  
  2021年12月25日 15:38
  
  电极对电子也会有散射的，以“自能”的形式考虑进去了
  
  回复
匿名说道：

2021年12月17日 16:43

博主您好，我想问一下有的时候H01不存在逆，这时候该咋办？

回复
1. guanjihuan说道：
  
  2021年12月17日 18:45
  
  对角线上加无穷小量，或者换一种编号方式。
  
  回复
zhangjiayan说道：

2021年12月9日 21:37

博主您好，首先感谢您分享那么多的知识和代码。然后我有一个问题想请教您。我目前在画外尔体系的霍尔电导，我是利用非平衡格林函数方法，根据Landauer-Buttiker公式来获得体系霍尔电导。然后我的电极选择的是利用金属电极。我想问一下，就是我们在计算霍尔电导的时候(也就是计算表面格林函数的时候)，四个端口是不是各自要设置一个费米能啊？如果要，请问该如何设置啊？

回复
1. guanjihuan说道：
  
  2021年12月10日 20:52
  
  看你考虑的是什么情况了。可以看下Datta的这本书《Electronic Transport In Mesoscopic Systems》。这是摘抄于第42页：For linear response we conceptually let the bias tend to zero; that is,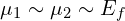 $\mu_1 \sim \mu_2\sim E_f$ .
  如果考虑大偏压，费米能可以取为固定，改变电极的on-site值，参照这篇文章的做法：Quantized four-terminal resistances in a ferromagnetic graphene p–n junction。另外也可以直接改变费米能来计算。我做了简单的数值验证，两种方法好像是等价的，因为求出的电极自能是相同的。
  
  回复
  1. 匿名说道：
    
    2021年12月10日 22:14
    
    好的，非常感谢，我仔细看看这篇文章！！！
    
    回复
    1. zhangjiayan说道：
      
      2021年12月14日 19:38
      
      博主您好，首先感谢您之前的回答，我下去也进行了验证。然后我想再请教一个问题。就是根据Landaur-Buttiker公式来计算霍尔电导，那编代码的时候该如何考虑每个端口的电压啊？我是通过调节端口的费米能，然后端口的费米能调来调去，但还是无法完全和文献相对应，总是差一截。
      
      回复
      1. guanjihuan说道：
        
        2021年12月15日 00:03
        
        我也不清楚，没算过这方面的。具体得看器件的设计吧，文献中应该会说明。也可以找其他文献看看。
        
        回复
        
        zhangjiayan说道：
        
        2021年12月15日 10:08
        
        好的，谢谢！
        
        回复
匿名说道：

2021年11月24日 11:07

博主您好！我想请教个问题。您在求表面格林函数的时候，根据镜面对称以及xy对称得到所有电极的表面格林函数是一样的，这里是不是因为左右的hopping以及xy方向的hopping都相同(您的代码参数设的是1)才可以，如果Tx≠Tx' Ty≠Ty'的话，就不能这样做了，而是需要每个电极求一次表面格林函数。

回复
1. guanjihuan说道：
  
  2021年11月25日 23:29
  
  是的。左右电极之所以用相同的表面格林函数，是因为h01等于h01^{dagger}。
  
  回复
  1. 匿名说道：
    
    2021年11月26日 10:30
    
    好的好的，非常感谢！
    
    回复

多端体系的量子输运（附Python代码）

一、代码1

二、代码2

三、代码3

Published by guanjihuan

25 thoughts on “多端体系的量子输运（附Python代码）”

发表评论取消回复

一、代码1

二、代码2

三、代码3

Published by guanjihuan

25 thoughts on “多端体系的量子输运（附Python代码）”

发表评论 取消回复

发表评论取消回复