1. Peierls substitution
在紧束缚模型中,磁场是通过Peierls substitution来引入的,即在跃迁项中多了一个相位
![]()
其中,![]() 表示的是磁通量子,
表示的是磁通量子,![]() 表示的是磁势,
表示的是磁势,![]() 表示的是坐标位置。
表示的是坐标位置。
这是之前的一篇:磁场和磁势的选取。这里以选取磁场为![]() 方向为例,磁势可以选为
方向为例,磁势可以选为![]() ,于是Peierls substitution可以写为:
,于是Peierls substitution可以写为:
![]()
其中,![]() 表示的是原子间距,
表示的是原子间距,![]() 表示的是在每个元格
表示的是在每个元格![]() 内磁通量子
内磁通量子![]() 的个数。
的个数。
额外说明:对于非方格子的情况,磁通B*S中的面积S一般是二维体系的元胞面积。例如:通过计算石墨烯中的Peierls substitution,可以发现只有凑出一个六角格子的面积,才能使得Hofstadter蝴蝶在满一个周期时,某个跃迁在每个元胞中的的相位始终都是2pi的整数倍。也就是说如果某个元胞的某个跃迁的相位是零,那么在下一个元胞的相同的位置相位应该为2pi,这样整体体系才会完全重复。具体参考:六角格子的佩尔斯替换和石墨烯条带的Hofstadter蝴蝶(附Python代码)。
2. 关于磁通量子的单位
根据公式![]() ,磁场的单位可以通过以下换算:
,磁场的单位可以通过以下换算:
![Rendered by QuickLaTeX.com \begin{aligned} 1T&=1N\cdot s/(C \cdot m)\\&=1N \cdot m \cdot s/(C \cdot m^2)\\&=1J \cdot s/(C \cdot m^2)\\&=\frac{1}{1.60217663410\times 10^{-19}}eV \cdot s/(C \cdot m^2)\\&=\frac{1}{1.60217663410\times 10^{-1}}eV \cdot s/[C \cdot (nm)^2]\\&=6.24150907407eV \cdot s/[C \cdot (nm)^2]\end{aligned}](https://www.guanjihuan.com/wp-content/ql-cache/quicklatex.com-6010baf55325204618c3609561889341_l3.png)
磁通量单位:![]()
普朗克常数![]() 的单位:
的单位:![]() 或
或![]()
磁通量子![]() 的单位与磁通量的单位一致。
的单位与磁通量的单位一致。
3. 关于磁通量子的大小
普朗克常数:![]()
电荷:![]()
磁通量子:

此外,磁通量子在文献中也经常定义为:
![]()
4. 每个元格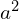 内磁通量子
内磁通量子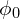 的个数
的个数
假设![]() ,磁场
,磁场![]() ,每个元格
,每个元格![]() 内磁通量子
内磁通量子![]() 的个数:
的个数:
![Rendered by QuickLaTeX.com \begin{aligned}n_z=\frac{Ba^2}{\phi_0}&=\frac{1T\times 1(nm)^2}{2.58128074575\times 10^{4}eV\cdot s/C}\\&=\frac{6.24150907407eV \cdot s/[C \cdot (nm)^2]\times 1(nm)^2}{2.58128074575\times 10^{4}eV\cdot s/C}\\&=2.4179892421 \times 10^{-4}\end{aligned}](https://www.guanjihuan.com/wp-content/ql-cache/quicklatex.com-7c0229dae9bd5009aff277df0c9ce155_l3.png)
5. 磁场大小的选取
在数值上,磁场一般选取为: ![]() 。 其中,
。 其中,![]() 是在数值上赋予的无量纲值。
是在数值上赋予的无量纲值。
当![]() ,原子间距
,原子间距![]() ,那么对应的实际磁场大小为
,那么对应的实际磁场大小为
![Rendered by QuickLaTeX.com \begin{aligned}B&=\frac{1}{c}\frac{\phi_0}{a^2}\\&=\frac{1}{1}\frac{2.58128074575\times 10^{4}eV\cdot s/C}{1(nm)^2}|\\&=2.58128074575\times 10^{4}eV\cdot s/[C \cdot (nm)^2]\\&=\frac{2.58128074575\times 10^{4}}{6.24150907407}T\\&=4.1356677\times 10^{3}T\end{aligned}](https://www.guanjihuan.com/wp-content/ql-cache/quicklatex.com-0cc45a7c64670dc3aaaa9a4c5a81e178_l3.png)
- 当原子间距
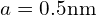 ,
,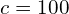 (
(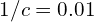 ),对应的实际磁场大小为
),对应的实际磁场大小为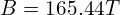 。
。 - 当原子间距
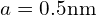 ,
,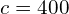 (
(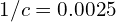 ),对应的实际磁场大小为
),对应的实际磁场大小为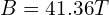 。
。 - 当原子间距
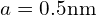 ,
,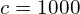 (
(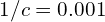 ),对应的实际磁场大小为
),对应的实际磁场大小为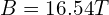 。
。 - 当原子间距
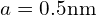 ,
,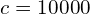 (
(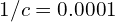 ),对应的实际磁场大小为
),对应的实际磁场大小为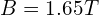 。
。 - 当原子间距
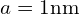 ,
,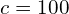 (
(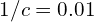 ),对应的实际磁场大小为
),对应的实际磁场大小为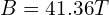 。
。 - 当原子间距
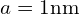 ,
,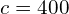 (
(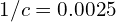 ),对应的实际磁场大小为
),对应的实际磁场大小为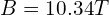
- 当原子间距
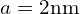 ,
,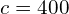 (
(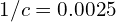 ),对应的实际磁场大小为
),对应的实际磁场大小为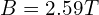 。
。
参考资料:
[1] R. E. Peierls, Z. Phys. 80, 763 (1933)
[2] Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields
[4] Magnetic-field effects on localization in a fractal lattice
[5] Magnetoconductance of the quantum spin Hall state
[6] 百度百科:普朗克常数
[7] 百度百科:磁通量量子
[8] 百度百科:基本电荷
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】
请问连续模型离散化也可以用佩尔斯替换加磁场吗
感谢
离散化后类似于晶格模型, 是可以加磁场的,得到的物理性质一般是指那个连续模型的K点的性质。但连续模型离散化这个近似操作,有的人可能无法接受,只能说研究得到的结论在某种程度上可以成立。
谢谢
老师想请教一下转角双层过度金属二硫化物加上垂直磁场,还可以画全空间的能带图吗
如果有周期性重复单元,即元胞,那么可以画能带。加了磁场,不过是把元胞变成了磁元胞,元胞大小会变大(和取的最小磁场有关)。
博主你好,请问第五点的c是怎么出现的?
c相当于数值计算中磁场B的取值,也就是一个量子磁通的1/c倍。如果c为1,表示的是磁场的选取刚好使得磁通为一个量子。
博主您好!我在文献时有一个疑问,请问peierls substitution和将磁矢势考虑到动量之内这两种方法有什么关系吗?谢谢您!
我认为是一回事,一个是从实空间角度来说,一个是从倒空间角度来说。应该是等价的,你可以找找文献看有没有相关证明,证明过程可能是从薛定谔方程出发的。
以下是在ChatGPT官网问询后生成的内容:
Peierls substitution(佩里尔斯替换)和将磁矢势考虑到动量之内这两种方法在一定程度上是相关的。
Peierls substitution 是一种用于处理带电粒子在存在磁场的情况下的量子力学问题的技巧。在使用该技巧时,我们将哈密顿量中的矢势替换为一个空间位置相关的相位因子,这个相位因子描述了粒子在电磁场中运动时积累的相位。这个相位因子的形式与将磁矢势考虑到动量之内时出现的相位因子是非常相似的。
在将磁矢势考虑到动量之内时,我们将哈密顿量中的动量项 $p$ 替换为 $p-eA/c$,其中 $A$ 是磁矢势,$c$ 是光速,$e$ 是元电荷。这个替换同样涉及到一个相位因子,即 $\exp(-ie\int A\cdot ds/\hbar)$,这个相位因子与 Peierls substitution 中的相位因子的形式非常相似。
因此,可以说 Peierls substitution 是将磁矢势考虑到动量之内这种方法的一种等效表述。两种方法都是为了描述带电粒子在磁场中的运动时积累的相位。不过,它们的应用场景和具体形式还是有所不同的。
这个磁场大小的选取是什么意思,指的是能产生磁通量子化带来的可观测效应的临界磁场?
不是,是指在数值计算上选取的值和真实磁场的关系
如果体系有内禀自旋轨道耦合,在次近邻跃迁项上会多一个相位吗
会的,形式差不多,有的相位可能是pi/2。参考:
[1] Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the "Parity Anomaly"
[2] Z 2 Topological Order and the Quantum Spin Hall Effect
关于Peierls substitution和Peierls tight-binding model 有课参考的数目或文献吗
参考资料已经列出来了。其他的资料应该有很多,可以自行搜索,例如:https://topocondmat.org/w2_majorana/Peierls.html。
请问这句话是什么意思(某个跃迁在每个元胞中的的相位始终都是2pi的整数倍)?对于方格子在一个原胞一周的相位是2*pi*nz/a吗?
当磁场加到一定的值时,会进入下一个Hofstadter蝴蝶周期,这时候整个体系应该是完全一样的。在这个新周期,如果某个元胞的某个跃迁的相位是零,那么在下一个元胞的相同的位置相位应该为2pi,这样才会完全重复。
方格子元胞一周的相位应该是2*pi*nz。