在介观体系中,两端口的电导由Landauer公式给出[1]:
![]()
其中,![]() 表示电子的透射几率(transmission)。
表示电子的透射几率(transmission)。
推广到多端口体系,有Landauer–Büttiker公式[1]:
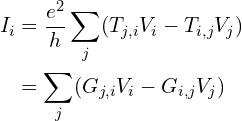
其中,![]() 也可以写为
也可以写为![]() ,表示的是从第
,表示的是从第![]() 个端口散射到第
个端口散射到第![]() 个端口的几率。
个端口的几率。
一、四端口
以四端口体系为例,上面的公式可以写为矩阵形式:
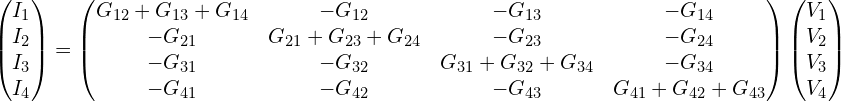
其中矩阵对角线上用到了以下关系:
![]()
该关系式的证明如下:当所有电极的电压都相等时,在![]() 端的电极的电流
端的电极的电流![]() 应为零,代入Landauer–Büttiker公式,证毕。
应为零,代入Landauer–Büttiker公式,证毕。
电极形状可定义为:
lead1 lead3
lead4
一般可令![]() ,
,![]() 。表达式写为:
。表达式写为:
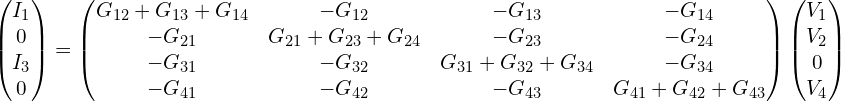
在强磁场下(朗道能级)或只存在边缘态的情况下,假设电流只有从1->2->3->4->1这个过程,以上可化简为:
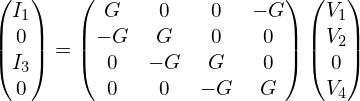
其中,![]() 。“2”来源于电子的自旋自由度,“M”表示通道数。
。“2”来源于电子的自旋自由度,“M”表示通道数。
展开得:
得到:![]() ,
, ![]() ,
,![]() 。
。
所以霍尔电阻:![]() 。
。
二、六端口
以下考虑六端口。公式显示比较小,可在公式上右键,选择“在新标签页中打开图像”。
六端口的形式:
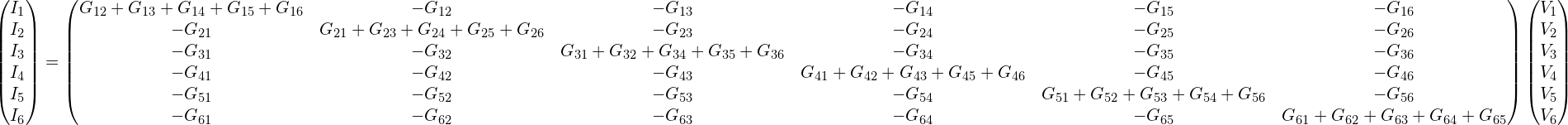
电极形状可定义为:
lead1 lead4
lead6 lead5
一般可令![]() ,
,![]() 。表达式写为:
。表达式写为:
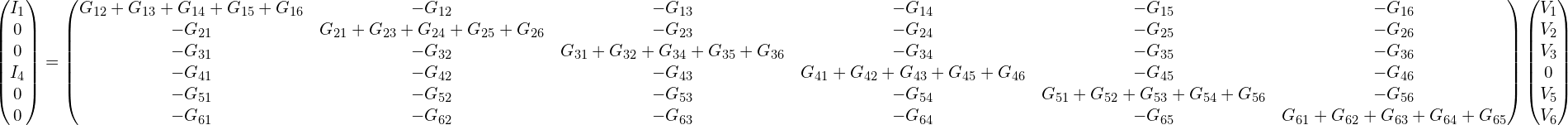
强磁场下(朗道能级)或只存在边缘态的情况下,假设电流只有从1->2->3->4->5->6->1这个过程,以上可化简为:
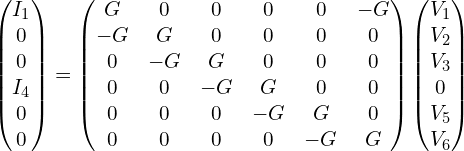
展开得:
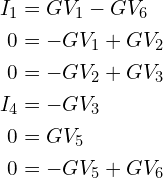
得到:![]() ,
,![]() ,
,![]() 。
。
所以霍尔电阻:![]() 。
。
补充说明:如果没有使得某些矩阵元为零,那么推导霍尔电阻或纵向电阻似乎有点难度。
参考资料:
[1] Supriyo Datta, Electronic transport in mesoscopic systems, 2004.
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】
您好,对于多端口,可以是奇数的情况吗,比如3,5,是否能用kwant去计算电导,谢谢。
也是可以的,按Kwant官方文档中的方法添加电极。
博主,对于多端口体系,任意两个端口的电导与其透射率还是(e^2/h)倍的关系么?
由于存在电极的散射,所以无法达到绝对的(e^2/h)倍。如果把所有透射和反射全部加起来,还是(e^2/h)倍。