BHZ模型的自旋陈数和Z2不变量（附Python、Matlab代码）

发布时间：2020年9月5日2022年7月14日

最近修改时间：2022年7月14日

BHZ模型的能带图参考：BHZ模型哈密顿量与准一维体系的能带图（附Python代码）。

BHZ模型哈密顿量：

$H_{\mathrm{eff}}(k_x, k_y)= \begin{pmatrix} H(k) & 0 \\ 0 & H^{*}(-k) \\ \end{pmatrix}$

$H(k)= \varepsilon(k)+d_i(k) \sigma_i$

$d_1+id_2=A[\sin(k_x)+i\sin(k_ y)]$

$d_3=-2B[2-(M/2B)-\cos(k_x)-\cos(k_y)]$

$\varepsilon(k)=C-2D[2-\cos(k_x)-\cos(k_y)]$

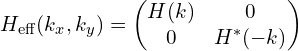
一、自旋陈数

因为自旋向上和自旋向下是两个相互独立的子体系（对应的陈数刚好相反），自旋是守恒的，因此可以定义自旋陈数。

陈数的计算方法为：陈数Chern number的计算（高效法，附Python/Matlab代码）。

代码如下：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/5778
"""

import numpy as np
import matplotlib.pyplot as plt
from math import *   # 引入pi, cos等
import cmath
import time


def hamiltonian1(kx, ky):  # Half BHZ for spin up
    A=0.3645/5
    B=-0.686/25
    C=0
    D=-0.512/25
    M=-0.01
    matrix = np.zeros((2, 2))*(1+0j) 
    varepsilon = C-2*D*(2-cos(kx)-cos(ky))
    d3 = -2*B*(2-(M/2/B)-cos(kx)-cos(ky))
    d1_d2 = A*(sin(kx)+1j*sin(ky))

    matrix[0, 0] = varepsilon+d3
    matrix[1, 1] = varepsilon-d3
    matrix[0, 1] = np.conj(d1_d2)
    matrix[1, 0] = d1_d2 
    return matrix

def hamiltonian2(kx, ky):  # Half BHZ for spin down
    A=0.3645/5
    B=-0.686/25
    C=0
    D=-0.512/25
    M=-0.01
    matrix = np.zeros((2, 2))*(1+0j) 
    varepsilon = C-2*D*(2-cos(-kx)-cos(-ky))
    d3 = -2*B*(2-(M/2/B)-cos(-kx)-cos(-ky))
    d1_d2 = A*(sin(-kx)+1j*sin(-ky))

    matrix[0, 0] = varepsilon+d3
    matrix[1, 1] = varepsilon-d3
    matrix[0, 1] = d1_d2 
    matrix[1, 0] = np.conj(d1_d2)
    return matrix


def main():
    start_clock = time.perf_counter()
    delta = 0.1 
    for i0 in range(2):
        if i0 == 0:
            hamiltonian = hamiltonian1
        else:
            hamiltonian = hamiltonian2
        chern_number = 0  # 陈数初始化
        for kx in np.arange(-pi, pi, delta):
            print(kx)
            for ky in np.arange(-pi, pi, delta):
                H = hamiltonian(kx, ky) 
                eigenvalue, eigenvector = np.linalg.eig(H)
                vector = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 价带波函数
            
                H_delta_kx = hamiltonian(kx+delta, ky) 
                eigenvalue, eigenvector = np.linalg.eig(H_delta_kx)
                vector_delta_kx = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]   # 略偏离kx的波函数

                H_delta_ky = hamiltonian(kx, ky+delta)  
                eigenvalue, eigenvector = np.linalg.eig(H_delta_ky)
                vector_delta_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 略偏离ky的波函数
                
                H_delta_kx_ky = hamiltonian(kx+delta, ky+delta)  
                eigenvalue, eigenvector = np.linalg.eig(H_delta_kx_ky)
                vector_delta_kx_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 略偏离kx和ky的波函数
                
                Ux = np.dot(np.conj(vector), vector_delta_kx)/abs(np.dot(np.conj(vector), vector_delta_kx))
                Uy = np.dot(np.conj(vector), vector_delta_ky)/abs(np.dot(np.conj(vector), vector_delta_ky))
                Ux_y = np.dot(np.conj(vector_delta_ky), vector_delta_kx_ky)/abs(np.dot(np.conj(vector_delta_ky), vector_delta_kx_ky))
                Uy_x = np.dot(np.conj(vector_delta_kx), vector_delta_kx_ky)/abs(np.dot(np.conj(vector_delta_kx), vector_delta_kx_ky))

                F = cmath.log(Ux*Uy_x*(1/Ux_y)*(1/Uy))
                # 陈数(chern number)
                chern_number = chern_number + F
        chern_number = chern_number/(2*pi*1j)
        if i0 == 0:
            chern_number_up = chern_number
        else:
            chern_number_down = chern_number
    spin_chern_number = (chern_number_up-chern_number_down)/2
    print('Chern number for spin up = ', chern_number_up)
    print('Chern number for spin down = ', chern_number_down)
    print('Spin chern number = ', spin_chern_number)
    end_clock = time.perf_counter()
    print('CPU执行时间(min)=', (end_clock-start_clock)/60)


if __name__ == '__main__':
    main()

计算结果为：

二、Z2不变量

如果自旋不守恒，一般情况下自旋陈数失去了物理意义（但可以通过特殊的处理方式来定义自旋陈数，这里不进行讨论）。在时间反演对称性下可以定义Z2不变量，计算方法见参考资料[1-5]。

计算BHZ模型Z2不变量的代码（仍以自旋守恒的体系为例）：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/5778
"""

import numpy as np
import matplotlib.pyplot as plt
from math import *   # 引入pi, cos等
import cmath
import time


def hamiltonian(kx, ky):  # BHZ模型
    A=0.3645/5
    B=-0.686/25
    C=0
    D=-0.512/25
    M=-0.01
    matrix = np.zeros((4, 4))*(1+0j) 

    varepsilon = C-2*D*(2-cos(kx)-cos(ky))
    d3 = -2*B*(2-(M/2/B)-cos(kx)-cos(ky))
    d1_d2 = A*(sin(kx)+1j*sin(ky))
    matrix[0, 0] = varepsilon+d3
    matrix[1, 1] = varepsilon-d3
    matrix[0, 1] = np.conj(d1_d2)
    matrix[1, 0] = d1_d2 

    varepsilon = C-2*D*(2-cos(-kx)-cos(-ky))
    d3 = -2*B*(2-(M/2/B)-cos(-kx)-cos(-ky))
    d1_d2 = A*(sin(-kx)+1j*sin(-ky))
    matrix[2, 2] = varepsilon+d3
    matrix[3, 3] = varepsilon-d3
    matrix[2, 3] = d1_d2 
    matrix[3, 2] = np.conj(d1_d2)
    return matrix


def main():
    start_clock = time.perf_counter()
    delta = 0.1
    Z2 = 0  # Z2数
    for kx in np.arange(-pi, 0, delta):
        print(kx)
        for ky in np.arange(-pi, pi, delta):
            H = hamiltonian(kx, ky) 
            eigenvalue, eigenvector = np.linalg.eig(H)
            vector = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 价带波函数1
            vector2 = eigenvector[:, np.argsort(np.real(eigenvalue))[1]]  # 价带波函数2
        
            H_delta_kx = hamiltonian(kx+delta, ky) 
            eigenvalue, eigenvector = np.linalg.eig(H_delta_kx)
            vector_delta_kx = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]   # 略偏离kx的波函数1
            vector_delta_kx2 = eigenvector[:, np.argsort(np.real(eigenvalue))[1]]   # 略偏离kx的波函数2

            H_delta_ky = hamiltonian(kx, ky+delta)  
            eigenvalue, eigenvector = np.linalg.eig(H_delta_ky)
            vector_delta_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 略偏离ky的波函数1
            vector_delta_ky2 = eigenvector[:, np.argsort(np.real(eigenvalue))[1]]  # 略偏离ky的波函数2
            
            H_delta_kx_ky = hamiltonian(kx+delta, ky+delta)  
            eigenvalue, eigenvector = np.linalg.eig(H_delta_kx_ky)
            vector_delta_kx_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 略偏离kx和ky的波函数1
            vector_delta_kx_ky2 = eigenvector[:, np.argsort(np.real(eigenvalue))[1]]  # 略偏离kx和ky的波函数2
            
            Ux = dot_and_det(vector, vector_delta_kx, vector2, vector_delta_kx2)
            Uy = dot_and_det(vector, vector_delta_ky, vector2, vector_delta_ky2)
            Ux_y = dot_and_det(vector_delta_ky, vector_delta_kx_ky, vector_delta_ky2, vector_delta_kx_ky2)
            Uy_x = dot_and_det(vector_delta_kx, vector_delta_kx_ky, vector_delta_kx2, vector_delta_kx_ky2)

            F = np.imag(cmath.log(Ux*Uy_x*np.conj(Ux_y)*np.conj(Uy)))
            A = np.imag(cmath.log(Ux))+np.imag(cmath.log(Uy_x))+np.imag(cmath.log(np.conj(Ux_y)))+np.imag(cmath.log(np.conj(Uy)))
            Z2 = Z2 + (A-F)/(2*pi)
    print('Z2 = ', Z2)  # Z2数
    end_clock = time.perf_counter()
    print('CPU执行时间(min)=', (end_clock-start_clock)/60)


def dot_and_det(a1, b1, a2, b2): # 内积组成的矩阵对应的行列式
    x1 = np.dot(np.conj(a1), b1)
    x2 = np.dot(np.conj(a2), b2)
    x3 = np.dot(np.conj(a1), b2)
    x4 = np.dot(np.conj(a2), b1)
    return x1*x2-x3*x4


if __name__ == '__main__':
    main()

计算结果为：

在自旋守恒的情况下，自旋陈数和Z2不变量是一致的。

Matlab代码为（内容同上）：

% This code is supported by the website: https://www.guanjihuan.com
% The newest version of this code is on the web page: https://www.guanjihuan.com/archives/5778

clear;clc;
delta=0.1;
Z2=0; 
for kx=-pi:0.1:0
    for ky=-pi:0.1:pi
        [V1,V2]=get_vector(Hamiltonian(kx,ky));
        [Vkx1,Vkx2]=get_vector(Hamiltonian(kx+delta,ky)); % 略偏离kx的波函数
        [Vky1,Vky2]=get_vector(Hamiltonian(kx,ky+delta)); % 略偏离ky的波函数
        [Vkxky1,Vkxky2]=get_vector(Hamiltonian(kx+delta,ky+delta)); % 略偏离kx，ky的波函数
        
        Ux = dot_and_det(V1, Vkx1, V2, Vkx2);
        Uy = dot_and_det(V1, Vky1, V2, Vky2);
        Ux_y = dot_and_det(Vky1, Vkxky1, Vky2, Vkxky2);
        Uy_x = dot_and_det(Vkx1, Vkxky1, Vkx2, Vkxky2);
        
        F=imag(log(Ux*Uy_x*(conj(Ux_y))*(conj(Uy))));
        A=imag(log(Ux))+imag(log(Uy_x))+imag(log(conj(Ux_y)))+imag(log(conj(Uy)));
        
        Z2 = Z2+(A-F)/(2*pi);
    end
end
Z2= mod(Z2, 2)


function dd = dot_and_det(a1,b1,a2,b2)   % 内积组成的矩阵对应的行列式
x1=a1'*b1;
x2=a2'*b2;
x3=a1'*b2;
x4=a2'*b1;
dd =x1*x2-x3*x4;
end


function [vector_new_1, vector_new_2] = get_vector(H)
[vector,eigenvalue] = eig(H);
[eigenvalue, index]=sort(diag(eigenvalue), 'ascend');
vector_new_2 = vector(:, index(2));
vector_new_1 = vector(:, index(1));
end


function H=Hamiltonian(kx,ky)  % BHZ模型
A=0.3645/5;
B=-0.686/25;  
C=0;
D=-0.512/25;
M=-0.01;

H=zeros(4,4);
varepsilon = C-2*D*(2-cos(kx)-cos(ky));
d3 = -2*B*(2-(M/2/B)-cos(kx)-cos(ky));
d1_d2 = A*(sin(kx)+1j*sin(ky));
H(1, 1) = varepsilon+d3;
H(2, 2) = varepsilon-d3;
H(1, 2) = conj(d1_d2);
H(2, 1) = d1_d2 ;

varepsilon = C-2*D*(2-cos(-kx)-cos(-ky));
d3 = -2*B*(2-(M/2/B)-cos(-kx)-cos(-ky));
d1_d2 = A*(sin(-kx)+1j*sin(-ky));
H(3, 3) = varepsilon+d3;
H(4, 4) = varepsilon-d3;
H(3, 4) = d1_d2 ;
H(4, 3) = conj(d1_d2);
end

额外说明：代码严格来说可能还需要处理下高对称点和高对称线的情况，具体可以看参考资料中的说明。目前这个例子计算结果没有出现问题，估计是这些位置的数值刚好为零。

参考资料：

[1] Z2拓扑不变量与拓扑绝缘体

[2] Time reversal polarization and a Z2 adiabatic spin pump

[3] Chern number and Z2 invariant

[4] Quantum Spin Hall Effect in Three Dimensional Materials: Lattice Computation of Z₂ Topological Invariants and Its Application to Bi and Sb

[5] First-principles calculation of Z2topological invariants within the FP-LAPW formalism

6,228 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】

Published by guanjihuan

View all posts by guanjihuan

39 thoughts on “BHZ模型的自旋陈数和Z2不变量（附Python、Matlab代码）”

我搞不好real说道：

2024年12月7日 15:14

matlab代码的delta步长改变的话，Z2会错误，是为什么呀

回复
1. guanjihuan说道：
  
  2024年12月7日 20:11
  
  很有可能是要处理高对称点和高对称线的情况，当步长比较刚好时，会落在高对称点或高对称线上。这里代码没有处理，你可以根据文献中的说明对代码进行修改。
  
  回复
匿名说道：

2024年8月26日 23:39

老师您好，我有几个trivial的问题想请教一下。1）我看到您在计算自旋陈数时，对于spin-up 和spin-down部分的哈密顿量只是把k变成-k, 其他都不变，这样处理是为什么呢，是根据时间反演算符对态的作用来的吗？对于Kane_Mele 模型也可以这样算吗？如果两部分的能带有交叉，或者有Rashba SOC, 还可以这样分别算吗？

我在看文献时发现对于不同的模型，很多算符（比如C2, TRS, PHS等等）的形式都是不同的，如果我有一个已知哈密顿量，但是不知道对称性的模型，我要怎么构建它的各种算符呢？我可以把算符的矩阵元都设为未知数，然后根据反对易/对易关系列方程组，看它有没有解吗？

回复
1. guanjihuan说道：
  
  2024年8月27日 22:35
  
  （1）spin-up 和spin-down部分的哈密顿量的这个区别，确实是为了满足时间反演对称性。这个哈密顿量是由文献中给出的：Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells。
  （2）如果两部分不是独立的，那么不大好定义自旋陈数，通常用Z2数来描述，不能分开算。
  （3）时间反演等算符通常具有比较固定的形式；C2等晶体对称性的算符形式一般和哈密顿量的编号有关，从结构上能直接看出，然后可以给于一个对应的表达形式。你说的那个方法，方程组数量应该不够吧，无法求解所有的矩阵元。我对对称性的了解不是很多，你也可以查找一些文献，看看别人是怎么研究的。
  
  回复
  1. 匿名说道：
    
    2024年8月28日 20:44
    
    好的，非常感谢您的回复！
    
    回复
匿名说道：

2024年6月23日 00:18

关老师您好，非常感谢您的代码！我在用Wilson Loop 方法计算Chern number 时，出现了在一些高对称点得到本征向量为0的情况，请问应该怎么处理呢？我看到您标注了一些参考资料，但是没有从其中找到处理方法。

回复
1. guanjihuan说道：
  
  2024年6月23日 09:56
  
  本征向量不能为零向量，看下有没有算错。另外，在时间反演对称性下，计算时只对半个布里渊区积分，可能是需要绕过高对称点，可以看下参考文献[1]的图3。
  
  回复
  1. 匿名说道：
    
    2024年6月27日 05:21
    
    非常感谢您，我其实是在用Wilson Loop (简并能带) 情况计算自旋陈数，在高对称点会有单纯自旋向上或向下的情况，如果这个时候用自旋投影算符，就会得到为0的本征向量，请问这种情况应该怎么处理呢？
    
    回复
    1. guanjihuan说道：
      
      2024年6月27日 09:33
      
      这个我也不清楚，没法回答你的问题。按理来说，得到0的本征向量不是物理的结果，甚至不是数学的结果，本征向量不应该为0的。可以检查下公式，看投影的过程是否是对的，或者可能本身是不存在解。另外，对于简并的情况，波函数可能需要正交归一化处理一下。
      
      回复
匿名说道：

2024年4月23日 15:40

好的，感谢您的回复

回复
匿名说道：

2024年4月22日 22:54

您好，想问一下这里自旋陈数的计算看起来和陈数的计算是一样的，因为两个自旋的子空间是解耦的，所以可以分别计算，这样定义的自旋陈数和PHYSICAL REVIEW B 80, 125327, 2009自旋陈数的定义看起来是不同的

回复
1. guanjihuan说道：
  
  2024年4月22日 23:00
  
  是的，这里的定义只是对于解耦的情况才成立。通用的定义方式这里没给出来，感兴趣的可以自己算下。
  
  回复
魏某说道：

2022年11月6日 20:56

你好，请问一下对于BHZ模型，如何构造时间反演算符T，使得满足时间反演对称性TH_kT^{-1}=H_{-k}^*且T^2=-1

回复
1. guanjihuan说道：
  
  2022年11月6日 21:34
  
  大概跟这个差不多，这个算符矩阵是二维的：时间反演算符 Time Reversal Operator。
  如果这个算符矩阵和二阶的单位矩阵进行张量积就可以变成四维的，但要注意张量积的前后顺序，有一个顺序是对的，刚好和BHZ模型的分块形式对应上。张量积参考这篇：泡利矩阵以及泡利矩阵的张量积。
  
  回复
匿名说道：

2021年11月9日 17:09

请问如果我要算的哈密顿有四条价带，function dd = dot_and_det(a1,b1,a2,b2) % 内积组成的矩阵对应的行列式
x1=a1'*b1;
x2=a2'*b2;
x3=a1'*b2;
x4=a2'*b1;
dd =x1*x2-x3*x4;
end
那么这个偏函数里求得dd，应该是8X8的矩阵的行列式吗

回复
1. guanjihuan说道：
  
  2021年11月10日 19:05
  
  是2x2矩阵的行列式。内积后是一个数，不是矩阵。
  
  回复
匿名说道：

2021年11月9日 16:28

[eigenvalue, index]=sort(diag(eigenvalue), 'ascend');
vector_new_2 = vector(:, index(2));
vector_new_1 = vector(:, index(1));
请问楼主上面的代码是取了导带来计算吗，取价带3，4来算的话会不会Z2是相反数啊

回复
1. guanjihuan说道：
  
  2021年11月10日 19:01
  
  取的是价带。ascend是上升的意思，最前面两个带是价带。另外两条带我没考虑过，你可以算算。理论上如果考虑所有的带，Z2应该等于0。
  
  回复
  1. 匿名说道：
    
    2021年11月28日 10:39
    
    请问这里取的两条带必须要是不同自旋贡献的兼并的两条带吗，要算Z2是不是模型必须要有这个自由度啊
    
    回复
    1. guanjihuan说道：
      
      2021年11月28日 19:40
      
      如果算自旋陈数，那么需要两个自旋是独立的。算Z2没有这个要求。
      至于Z2是否必须考虑自旋，目前我看到的都是有考虑，且需要满足时间反演对称性。其他情况我不是很了解，没深入研究过，你可以查下文献看看。
      
      回复
      1. 匿名说道：
        
        2021年11月29日 16:36
        
        多谢指导
        
        回复
匿名说道：

2021年11月9日 16:20

请问bhz模型的陈数是两个自旋陈数之和（-1）+（1）=0吗

回复
1. guanjihuan说道：
  
  2021年11月10日 18:56
  
  不是之和，是相减后除以2。
  
  回复
灰色XT说道：

2020年11月26日 18:33

作者可以出一篇运用wannier function center的计算Z2不变量的文章吗？然后比较说明一下和用贝里曲率算法的比较说明，这两个方法的对比，看了文献，并不是非常的理解。谢谢

回复
1. guanjihuan说道：
  
  2020年11月26日 19:43
  
  这方面的文章我看的也不多，目前不是很了解。之后有空的时候可能会考虑。你可以多找些文献看看，看不同文献中的描述。
  
  回复
杨柠境说道：

2020年11月26日 14:58

请问这里面的积分空间是根据什么来选取的呢？

回复
1. guanjihuan说道：
  
  2020年11月26日 18:51
  
  如果是计算Z2不变量，在这个方法中是选取一半的布里渊区。
  
  回复
  1. 杨柠境说道：
    
    2020年11月26日 19:43
    
    嗯嗯，是的。对于简单的BHZ正方晶格的积分选取是比较显而易见的。那如果对于非正方晶格比如三角晶格或六角晶格，就会出现缺角啊，还是说根据话高对称点之间的能带图的取法来选取呢？
    
    回复
    1. guanjihuan说道：
      
      2020年11月26日 19:52
      
      一样的，可以通过程序把积分限制半个布里渊内，不管是什么图形。
      
      回复
      1. 杨柠境说道：
        
        2020年11月27日 20:14
        
        如何还是按照离散矩阵的形式来积分吗？
        
        回复
        
        guanjihuan说道：
        
        2020年11月28日 04:58
        
        可以参考这一篇中的积分方法：Haldane模型中陈数的计算（附Python代码）
        
        回复
灰色XT说道：

2020年11月23日 22:22

作者可以出一个matlab的求Z2不变量的参考程序吗？谢谢

回复
1. guanjihuan说道：
  
  2020年11月24日 18:29
  
  在博文的最后更新了matlab代码，供参考。内容是一样的。
  
  回复
  1. 杨柠境说道：
    
    2020年11月24日 19:30
    
    十分感谢博主，对于一个初次接触拓扑的研究生帮助甚大，希望可以多交流。
    
    回复
匿名说道：

2020年11月23日 17:11

博主您好，我想请问一下，对于这样的二能带系统，里面的A具体是怎么定义的，能展开说说吗？因为对于二能带，A（联络）应该是矩阵形式，那么对应于U，U的具体形式是怎么样的呢？看程序看的不太明显…麻烦了

回复
1. guanjihuan说道：
  
  2020年11月23日 18:09
  
  公式参考这篇中给的文献：陈数Chern number的计算（高效法，附Python/Matlab代码）。A或U都是标量吧，不是矩阵，内积的结果是一个值。
  
  回复
  1. 匿名说道：
    
    2020年11月23日 18:47
    
    能带有两个指标很明显A的分量为A11，A12，A21，A22，数字为能带指标啊…为啥不是矩阵呢
    
    回复
    1. guanjihuan说道：
      
      2020年11月23日 23:13
      
      是有形成一个矩阵，不同能带上的波函数是正交的，非对角线上的矩阵元（内积值）应该为零。U最后是取了一个行列式，具体公式你可以参照参考资料[2]的PPT，或者其他参考资料。我对这方面也没有仔细研究过，只是简单算了下。
      
      回复
      1. 匿名说道：
        
        2021年11月9日 22:58
        
        参考文献3中的6式，内积的两个波函数分别是两个相似变换矩阵（2n列向量排列形成），两个方阵相乘再求行列式，
        应该是这样不，感觉和代码里不一样
        
        回复

一、 自旋陈数

二、Z2不变量

Published by guanjihuan

39 thoughts on “BHZ模型的自旋陈数和Z2不变量（附Python、Matlab代码）”

发表评论 取消回复

一、自旋陈数

发表评论取消回复