粒子-空穴对称性 Particle-Hole Symmetry

发布时间：2020年8月9日2024年3月3日

最近修改时间：2024年3月3日

1. 定义

粒子-空穴对称性体系的哈密顿量满足：

$\hat{P}\hat{H}\hat{P}^{\dagger}=-\hat{H}$

其中， $\hat{P}$ 为反幺正算符。对于两带体系，粒子-空穴对称性（particle-hole symmetry）算符可以写为 $\hat{P}=\sigma_x K$ 。 $K$ 是取复数的算符； $\sigma_x$ 是泡利矩阵，作用在粒子和空穴的矩阵元或子矩阵上。关于反幺正算符可以参照这篇：时间反演算符 Time Reversal Operator。

粒子-空穴对称性一般出现在超导中。BdG（ Bogoliubov-de Gennes）模型的哈密顿量为

$\hat{H}_{BdG}=\begin{pmatrix}H & \Delta\\-\Delta^{*} & -H^{*}\\\end{pmatrix}$

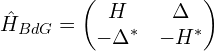
该哈密顿量完全满足粒子-空穴对称性。泡利矩阵作用在矩阵上可参考这篇：矩阵两边乘上向量或者泡利矩阵后的形式。 $\sigma_x$ 的作用使得：矩阵对角线的两个元素互换，非对角线的两个元素互换。此外，再考虑上取复数算符 $K$ 的作用。

2. 能谱

和手征对称性 Chiral Symmetry类似，满足粒子-空穴对称性的体系也有上下对称的能带。

假设 $|\psi \rangle$ 为具有粒子-空穴对称性的哈密顿量的波函数，对应本征值为 $E$ ，即

$\hat{H}|\psi \rangle=E|\psi \rangle$

那么 $\hat{P}|\psi \rangle$ 也是该哈密顿量的波函数，且对应的本征值为 $-E$ ，这是因为

$\hat{H}\hat{P}|\psi \rangle=-\hat{P}\hat{H}|\psi \rangle=-\hat{P} E|\psi \rangle=-E \hat{P} |\psi \rangle$

其中，第一步推导用到了上面粒子-空穴对称性的定义。

3. 总结

Time-reversal symmetry (T), particle-hole symmetry (P) and chiral symmetry (C) [3,4,5]：

其他：Rice-Mele模型

从SSH模型可以推广到Rice-Mele模型，Rice-Mele哈密顿量写为

$\hat{H}(k)=\begin{pmatrix} m & h(k)\\ h^*(k) & -m\\ \end{pmatrix}, \quad h(k)=d_x-id_y$

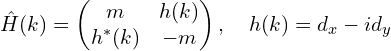
Rice-Mele模型满足时间反演对称性，不满足手征对称性和粒子空穴对称性，但它的能带也是上下对称的。

关于Rice-Mele模型的对称性可以阅读这篇文献（由马超同学提供）：Topological features of ground states and topological solitons in generalized Su-Schrieffer-Heeger models using generalized time-reversal, particle-hole, and chiral symmetries。在这篇文献中给出的是：PT-symmetric particle-hole and chiral symmetry. 文献截图为：

说明：之前在这里贴出的内容有误，已做删除，感谢马超同学提供的文献和讨论。

参考资料：

[1] https://topocondmat.org/w1_topointro/0d.html

[2] A Short Course on Topological Insulators: Band-structure topology and edge states in one and two dimensions

[3] https://topocondmat.org/w8_general/classification.html

[4] 手征对称性 Chiral Symmetry

[5] 时间反演算符 Time Reversal Operator

6,734 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】

Published by guanjihuan

View all posts by guanjihuan

10 thoughts on “粒子-空穴对称性 Particle-Hole Symmetry”

匿名说道：

2024年3月1日 10:49

BDG哈密顿里，左下角配对势为什么有个负号

回复
1. guanjihuan说道：
  
  2024年3月3日 07:23
  
  我也是觉得有点奇怪，不同地方写的不一样，这里的形式主要是为了满足粒子-空穴对称性，所以有个负号。
  
  我问了GPT，以下是机器给的回答，供参考，不一定是对的。可以多找几篇文献或书籍看看。
  
  ————————————————————————————
  
  两种形式的Bogoliubov-de Gennes (BdG) 哈密顿量都是正确的，只是它们针对系统的不同方面做了不同的描述。哪一个是更适合使用取决于你感兴趣的具体问题以及处理问题的数学方法。
  
  1. 第一个形式的BdG哈密顿量是：
  $\mathcal{H} = \begin{pmatrix} H_0 & \Delta \\ \Delta^\dagger & -H_0^* \end{pmatrix}$
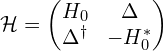
  在这个形式中，哈密顿量是一个厄米的矩阵。这种形式适用于许多问题，特别是当你需要研究超导/超流系统中的能谱和激发态时。
  
  2. 第二个形式的BdG哈密顿量是：
  $\hat{H}_{BdG}=\begin{pmatrix} H & \Delta\\ -\Delta^{*} & -H^{*}\\ \end{pmatrix}$
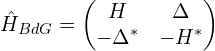
  在这个形式中，哈密顿量不是厄米的，但它仍然是一个有效的描述超导/超流系统的工具。这种形式适用于处理与超导/超流配对效应密切相关的问题。
  
  因此，哪个哈密顿量是正确的取决于你所研究的具体系统和问题的特性。
  
  回复
匿名说道：

2022年11月4日 18:21

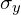请问 $\sigma_y$ 能当做ph对称性吗？

回复
1. guanjihuan说道：
  
  2022年11月6日 02:31
  
  这个我不清楚，你可以看文献中有没有用这个。常见的是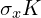 $\sigma_x K$ 。
  
  回复
匿名说道：

2022年9月23日 20:15

粒子空穴对称性是，电子和空穴互换后，系统保持不变，为什么这里哈密顿量前面要取负数

回复
1. guanjihuan说道：
  
  2022年9月24日 00:16
  嗯，物理上那么理解是对的。对称性表达式的为什么有个负号，可以参考这个答案：https://physics.stackexchange.com/questions/381328/why-particle-hole-symmetry-and-chiral-symmetry-are-called-symmetries。以及所给出的参考文献：
  
  Topological phases: classification of topological insulators and superconductors of non-interacting fermions, and beyond
  
  Topological insulators and superconductors: tenfold way and dimensional hierarchy
  回复
匿名说道：

2022年5月24日 22:30

请问知道对称性所满足的形式后（比如P*H*P'=-H），如何得到矩阵的具体形式（P=sigma_x*K）呢，不同模型下这个幺正矩阵的形式会不同吗

回复
1. guanjihuan说道：
  
  2022年5月24日 23:49
  
  好像不是唯一的，跟模型有关。对于BdG模型，粒子-空穴对称算符是这个表达式P=sigma_x*K。对于某个模型，具体怎么得到这个表达式，我也没做过深入调研和研究。
  
  回复
  1. 匿名说道：
    
    2022年5月25日 12:00
    
    BDG模型是从超导中提出来的吗，如果对于类SSH这种模型的话还一样吗
    
    回复
    1. guanjihuan说道：
      
      2022年5月25日 14:31
      
      嗯，BdG模型就是一个超导模型。说到粒子-空穴对称性，比较多的是谈到超导模型，因为有库伯对，电子和空穴是等价的。
      其他的模型可以查下文献看看，我也不了解。物理图像是清楚的，但具体表达式得根据哈密顿量的具体形式来讨论。
      
      回复