哈密顿量常见的三种形式

哈密顿量是一个算符，常见有以下三种形式：

1. 用Dirac记号表示

波函数可以写成Dirac记号： $\psi=|\psi \rangle$

对应的厄米共轭波函数为： $\psi=\langle \psi|$

内积： $\langle \phi|\psi \rangle=\int \phi^{*}(q) \psi(q) dq$

外积： $|\psi\rangle \langle \phi|$ ，表示为一个算符。

当 $\psi =\phi$ ，外积 $\hat{P}=|\psi \rangle \langle \psi|$ 也被称为投影算符。

在 $A$ 表象下，有一组正交归一的完备基 $\{|a_{i} \rangle\}$ ，满足

完备性： $\sum_{i} |a_i \rangle\langle a_i |= 1$

正交归一性： $\langle a_i | a_j \rangle = \delta_{ij}$

在该表象下，波函数写为：

$|\psi \rangle= \sum_{i} |a_i \rangle \langle a_i| \psi \rangle = \sum_{i} c_{i} |a_{i} \rangle$

在该表象下，算符写为：

$\begin{aligned}\hat{H}&=\sum_{i}|a_i \rangle \langle a_i|\hat{H} \sum_{j}|a_j \rangle \langle a_j|\\&=\sum_{ij}|a_i \rangle \langle a_i| \hat{H}|a_j \rangle \langle a_j|\\&=\sum_{ij}H_{ij} |a_i \rangle \langle a_j|\end{aligned}$

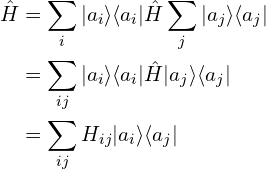
2. 用产生/湮灭算符来表示

在粒子数表象（二次量子化）下，单体算符 $\hat{H}=\sum_{i}\hat{h}(q_i)$ 可以写为：

$\hat{H}=\sum_{i j}h_{ij}\hat{c}_{i}^{\dagger}\hat{c}_j$

证明过程略。其中， $\hat{c}$ 是湮灭算符， $\hat{c}^{\dagger}$ 是产生算符，对于费米子系统，有 $\{\hat{c}_i, \hat{c}_j\}=\delta_{ij}$ 。系数为 $h_{ij}=\langle i|\hat{h}| j\rangle$ 。 $\hat{h}$ 表示的是某个粒子态对应的算符（单粒子态算符）。

需要说明的是：这里的表达式与第一种用Dirac记号表示的表达式十分类似，但这里表象是已经选定为粒子数表象，给出的表达式只适用于单体算符，如果是二体算符或者多体算符，表达式会更复杂一些。而第一种用Dirac记号表示的表达式是一般的、抽象的结论，适用于所有表象，其中基矢量 $\{|a_{i} \rangle\}$ 还没有给出具体的形式，要求是正交归一完备的即可。当表象选取为粒子数表象，同时只考虑单体问题时，这两种表示方式在物理上是等价的。

3. 用场算符来表示

场算符的定义为：

$\hat{\psi}(q)=\sum_{i} \hat{c}_{i}\psi_{i}(q)$

对应的厄米共轭场算符为：

$\hat{\psi}^{\dagger}(q)=\sum_{i} \hat{c}_{i}^{\dagger}\psi_{i}^{*}(q)$

单体算符 $\hat{H}=\sum_{i}\hat{h}(q_i)$ 可以写为：

$\hat{H}=\int \hat{\psi}^{\dagger}(q)\hat{h}(q)\hat{\psi}(q)dq$

其中， $\hat{h}(q)$ 表示的是某个粒子态对应的算符（单粒子态算符）。

证明：把定义式代入上述表达式，得到

$\begin{aligned}\hat{H}&=\int \hat{\psi}^{\dagger}(q)\hat{h}(q)\hat{\psi}(q)dq\\&=\int\sum_{i} \hat{c}_{i}^{\dagger}\psi_{i}^{*}(q)\hat{h}(q)\sum_{j} \hat{c}_{j}\psi_{j}(q)dq\\&=\sum_{ij}\hat{c}_{i}^{\dagger}\hat{c}_{j}\int\psi_{i}^{*}(q)\hat{h}(q)\psi_{j}(q)dq\\&=\sum_{ij}\langle i|\hat{h}| j\rangle \hat{c}_{i}^{\dagger}\hat{c}_{j}\\&=\sum_{ij}h_{ij} \hat{c}_{i}^{\dagger}\hat{c}_{j}\end{aligned}$

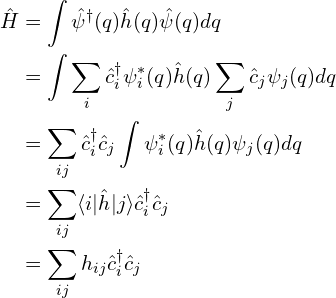
得到第二种用产生/湮灭算符来表示的表达式，证毕。

参考资料：

[1] 国科大金彪老师高等量子力学课堂笔记

[2] 季燕江《量子力学讲义》

[3] 百度百科：狄拉克符号

[4] 百度文库：P(四章第四讲)狄拉克符号

14,584 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】

4 thoughts on “哈密顿量常见的三种形式”

博主您好，请问里面的公式是怎么换行的啊？我使用了您推荐的，但是貌似worldpress下不识别latex中的&，导致我无法公式换行，您是怎么解决的？谢谢！

guanjihuan说道：

2021年1月31日 12:21

可以用aligned环境，例如：$$\begin{aligned} aligned&12345\\ &xyz\end{aligned}$$。也可以用array环境，或者矩阵环境。参考这篇：Latex公式常用符号

回复
1. 匿名说道：
  
  2021年1月31日 13:18
  
  我用的align环境，带公式排序的那种，前面加了那个latexpage，但是就是不换行也识别不了&，试了您的方法，虽然试别了&但是换行不对齐……
  
  回复
  1. guanjihuan说道：
    
    2021年1月31日 13:52
    
    换行需要两个反斜杠\\。对齐好像是需要每一行都有&。
    
    回复

哈密顿量常见的三种形式

1. 用Dirac记号表示

2. 用产生/湮灭算符来表示

3. 用场算符来表示

Published by guanjihuan

4 thoughts on “哈密顿量常见的三种形式”

发表评论取消回复

1. 用Dirac记号表示

2. 用产生/湮灭算符来表示

3. 用场算符来表示

Published by guanjihuan

4 thoughts on “哈密顿量常见的三种形式”

发表评论 取消回复

发表评论取消回复