Haldane模型中陈数的计算（附Python代码）

发布时间：2020年7月13日2022年9月15日

最近修改时间：2022年9月15日

之前一篇关于Haldane模型的博文：Haldane模型哈密顿量与能带图（附Python代码）。

在该博文中画出了Haldane模型条带（准一维）的能带，可以看到在体带隙中存在一个交叉的边缘态（可态密度验证属于边缘态）。该边缘态是受到拓扑保护的。本篇将给出Haldane模型中陈数的计算代码和计算结果。

方法仍然是采用这篇博文中的方法：陈数Chern number的计算（高效法，附Python/Matlab代码）。

一、积分方法1：限制积分范围在六角晶格内

需要注意的是，在方格子中，布里渊区是方格子，因此kx和ky的积分范围都在[-pi, pi]。而在六角格子中，布里渊区是六角格子，在写程序的时候需要对六角格子的布里渊区积分。

六角格子实空间中坐标位置为：

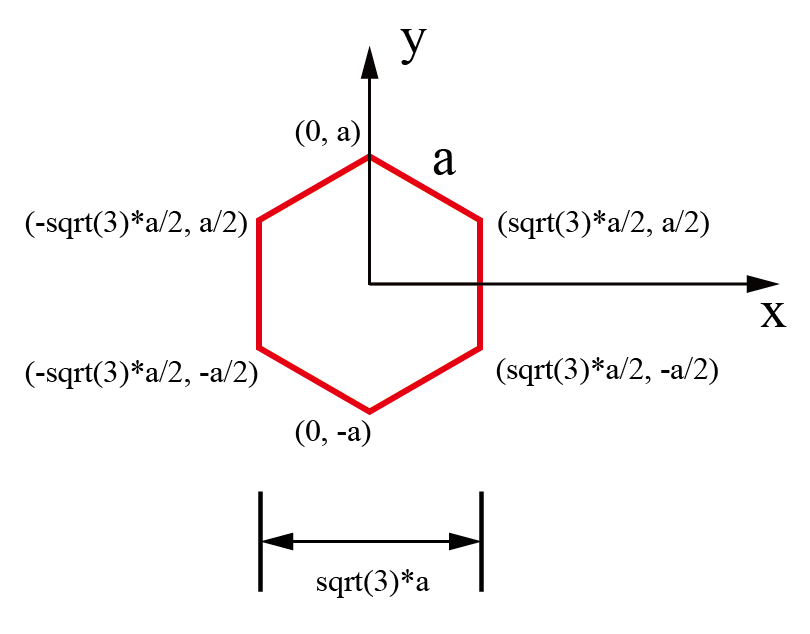
对应倒空间中的坐标为：

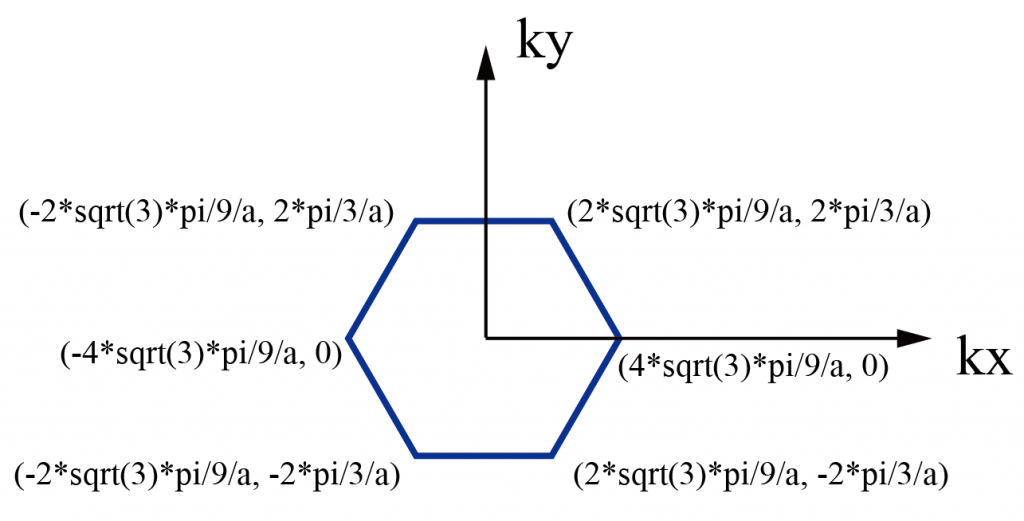
倒格子的坐标可参考：倒格子基矢的计算（附数值计算、符号计算Python代码）。

以下是计算Haldane模型陈数的Python代码，积分时要用判断语句限制在布里渊区内。

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/5133
"""

import numpy as np
from math import *   # 引入pi, cos等
import cmath
import time
import functools  # 使用偏函数functools.partial()


def hamiltonian(k1, k2, M, t1, t2, phi, a=1/sqrt(3)):  # Haldane哈密顿量（a为原子间距，不赋值的话默认为1/sqrt(3)）
    # 初始化为零矩阵
    h0 = np.zeros((2, 2), dtype=complex)
    h1 = np.zeros((2, 2), dtype=complex)
    h2 = np.zeros((2, 2), dtype=complex)

    # 质量项(mass term), 用于打开带隙
    h0[0, 0] = M
    h0[1, 1] = -M

    # 最近邻项
    h1[1, 0] = t1*(cmath.exp(1j*k2*a)+cmath.exp(1j*sqrt(3)/2*k1*a-1j/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j/2*k2*a))
    h1[0, 1] = h1[1, 0].conj()

    # # 最近邻项也可写成这种形式
    # h1[1, 0] = t1+t1*cmath.exp(1j*sqrt(3)/2*k1*a-1j*3/2*k2*a)+t1*cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a)
    # h1[0, 1] = h1[1, 0].conj()

    #次近邻项 # 对应陈数为-1
    h2[0, 0] = t2*cmath.exp(-1j*phi)*(cmath.exp(1j*sqrt(3)*k1*a)+cmath.exp(-1j*sqrt(3)/2*k1*a+1j*3/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a))
    h2[1, 1] = t2*cmath.exp(1j*phi)*(cmath.exp(1j*sqrt(3)*k1*a)+cmath.exp(-1j*sqrt(3)/2*k1*a+1j*3/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a))
    
    # # 次近邻项  # 对应陈数为1
    # h2[0, 0] = t2*cmath.exp(1j*phi)*(cmath.exp(1j*sqrt(3)*k1*a)+cmath.exp(-1j*sqrt(3)/2*k1*a+1j*3/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a))
    # h2[1, 1] = t2*cmath.exp(-1j*phi)*(cmath.exp(1j*sqrt(3)*k1*a)+cmath.exp(-1j*sqrt(3)/2*k1*a+1j*3/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a))

    matrix = h0 + h1 + h2 + h2.transpose().conj()
    return matrix


def main():
    start_clock = time.perf_counter()
    delta = 0.005
    chern_number = 0  # 陈数初始化
    
    # 几个坐标中常出现的项
    a = 1/sqrt(3)
    aa1 = 4*sqrt(3)*pi/9/a
    aa2 = 2*sqrt(3)*pi/9/a
    bb1 = 2*pi/3/a

    hamiltonian0 = functools.partial(hamiltonian, M=2/3, t1=1, t2=1/3, phi=pi/4, a=a)   # 使用偏函数，固定一些参数

    for kx in np.arange(-aa1, aa1, delta):
        print(kx)
        for ky in np.arange(-bb1, bb1, delta):
            if (-aa2<=kx<=aa2) or (kx>aa2 and -(aa1-kx)*tan(pi/3)<=ky<=(aa1-kx)*tan(pi/3)) or (kx<-aa2 and  -(kx-(-aa1))*tan(pi/3)<=ky<=(kx-(-aa1))*tan(pi/3)):  # 限制在六角格子布里渊区内

                H = hamiltonian0(kx, ky) 
                eigenvalue, eigenvector = np.linalg.eig(H)
                vector = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 价带波函数
            
                H_delta_kx = hamiltonian0(kx+delta, ky) 
                eigenvalue, eigenvector = np.linalg.eig(H_delta_kx)
                vector_delta_kx = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]   # 略偏离kx的波函数

                H_delta_ky = hamiltonian0(kx, ky+delta)  
                eigenvalue, eigenvector = np.linalg.eig(H_delta_ky)
                vector_delta_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 略偏离ky的波函数
                
                H_delta_kx_ky = hamiltonian0(kx+delta, ky+delta)  
                eigenvalue, eigenvector = np.linalg.eig(H_delta_kx_ky)
                vector_delta_kx_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 略偏离kx和ky的波函数
                
                Ux = np.dot(np.conj(vector), vector_delta_kx)/abs(np.dot(np.conj(vector), vector_delta_kx))
                Uy = np.dot(np.conj(vector), vector_delta_ky)/abs(np.dot(np.conj(vector), vector_delta_ky))
                Ux_y = np.dot(np.conj(vector_delta_ky), vector_delta_kx_ky)/abs(np.dot(np.conj(vector_delta_ky), vector_delta_kx_ky))
                Uy_x = np.dot(np.conj(vector_delta_kx), vector_delta_kx_ky)/abs(np.dot(np.conj(vector_delta_kx), vector_delta_kx_ky))

                F = cmath.log(Ux*Uy_x*(1/Ux_y)*(1/Uy))

                # 陈数(chern number)
                chern_number = chern_number + F

    chern_number = chern_number/(2*pi*1j)
    print('Chern number = ', chern_number)
    end_clock = time.perf_counter()
    print('CPU执行时间(min)=', (end_clock-start_clock)/60)


if __name__ == '__main__':
    main()

计算结果为：

如果改变相位phi的符号，对应的计算结果为：

当选取的积分步长越小，计算结果越接近1。因为这里是用Python写的，所以计算效率不会太高；如果用Fortran写，计算所耗的时间会更短些。

量子自旋霍尔效应中比较简单的情况是这样的：通过引入自旋，让一个自旋对应的陈数为-1，一个自旋对应的陈数为1，这时整体的陈数为0，满足时间反演不变性，需要引入Z2不变量。可参考博文：Kane-Mele模型的哈密顿量和能带图（不考虑Rashba自旋轨道耦合的情况）。

二、积分方法2：布里渊区平移成方形

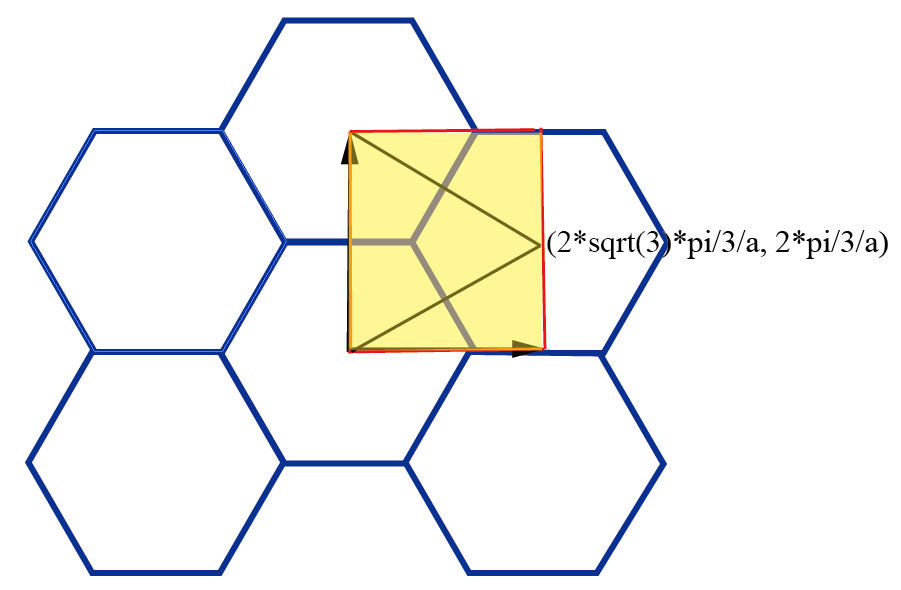
示意图如上所示。代码为：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/5133
"""

import numpy as np
import matplotlib.pyplot as plt
from math import *   # 引入pi, cos等
import cmath
import time
import functools  # 使用偏函数functools.partial()


def hamiltonian(k1, k2, M, t1, t2, phi, a=1/sqrt(3)):  # Haldane哈密顿量（a为原子间距，不赋值的话默认为1/sqrt(3)）
    # 初始化为零矩阵
    h0 = np.zeros((2, 2), dtype=complex)
    h1 = np.zeros((2, 2), dtype=complex)
    h2 = np.zeros((2, 2), dtype=complex)

    # 质量项(mass term), 用于打开带隙
    h0[0, 0] = M
    h0[1, 1] = -M

    # 最近邻项
    h1[1, 0] = t1*(cmath.exp(1j*k2*a)+cmath.exp(1j*sqrt(3)/2*k1*a-1j/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j/2*k2*a))
    h1[0, 1] = h1[1, 0].conj()

    # # 最近邻项也可写成这种形式
    # h1[1, 0] = t1+t1*cmath.exp(1j*sqrt(3)/2*k1*a-1j*3/2*k2*a)+t1*cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a)
    # h1[0, 1] = h1[1, 0].conj()

    #次近邻项 # 对应陈数为-1
    h2[0, 0] = t2*cmath.exp(-1j*phi)*(cmath.exp(1j*sqrt(3)*k1*a)+cmath.exp(-1j*sqrt(3)/2*k1*a+1j*3/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a))
    h2[1, 1] = t2*cmath.exp(1j*phi)*(cmath.exp(1j*sqrt(3)*k1*a)+cmath.exp(-1j*sqrt(3)/2*k1*a+1j*3/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a))
    
    # # 次近邻项  # 对应陈数为1
    # h2[0, 0] = t2*cmath.exp(1j*phi)*(cmath.exp(1j*sqrt(3)*k1*a)+cmath.exp(-1j*sqrt(3)/2*k1*a+1j*3/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a))
    # h2[1, 1] = t2*cmath.exp(-1j*phi)*(cmath.exp(1j*sqrt(3)*k1*a)+cmath.exp(-1j*sqrt(3)/2*k1*a+1j*3/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a))

    matrix = h0 + h1 + h2 + h2.transpose().conj()
    return matrix


def main():
    start_clock = time.perf_counter()
    delta = 0.005
    chern_number = 0  # 陈数初始化
    
    # 常出现的项
    a = 1/sqrt(3)
    bb1 = 2*sqrt(3)*pi/3/a
    bb2 = 2*pi/3/a

    hamiltonian0 = functools.partial(hamiltonian, M=2/3, t1=1, t2=1/3, phi=pi/4, a=a)   # 使用偏函数，固定一些参数

    for kx in np.arange(0 , bb1, delta):
        print(kx)
        for ky in np.arange(0, 2*bb2, delta):
            H = hamiltonian0(kx, ky) 
            eigenvalue, eigenvector = np.linalg.eig(H)
            vector = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 价带波函数
        
            H_delta_kx = hamiltonian0(kx+delta, ky) 
            eigenvalue, eigenvector = np.linalg.eig(H_delta_kx)
            vector_delta_kx = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]   # 略偏离kx的波函数

            H_delta_ky = hamiltonian0(kx, ky+delta)  
            eigenvalue, eigenvector = np.linalg.eig(H_delta_ky)
            vector_delta_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 略偏离ky的波函数
            
            H_delta_kx_ky = hamiltonian0(kx+delta, ky+delta)  
            eigenvalue, eigenvector = np.linalg.eig(H_delta_kx_ky)
            vector_delta_kx_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 略偏离kx和ky的波函数
            
            Ux = np.dot(np.conj(vector), vector_delta_kx)/abs(np.dot(np.conj(vector), vector_delta_kx))
            Uy = np.dot(np.conj(vector), vector_delta_ky)/abs(np.dot(np.conj(vector), vector_delta_ky))
            Ux_y = np.dot(np.conj(vector_delta_ky), vector_delta_kx_ky)/abs(np.dot(np.conj(vector_delta_ky), vector_delta_kx_ky))
            Uy_x = np.dot(np.conj(vector_delta_kx), vector_delta_kx_ky)/abs(np.dot(np.conj(vector_delta_kx), vector_delta_kx_ky))

            F = cmath.log(Ux*Uy_x*(1/Ux_y)*(1/Uy))
            # 陈数(chern number)
            chern_number = chern_number + F

    chern_number = chern_number/(2*pi*1j)
    print('Chern number = ', chern_number)
    end_clock = time.perf_counter()
    print('CPU执行时间(min)=', (end_clock-start_clock)/60)


if __name__ == '__main__':
    main()

计算结果为：

三、积分方法3：坐标变换

此外，还有一种计算六角格子的方法，是直接对六角格子的基矢做积分。这个计算方法是由知乎网友“青春银河”提供：

“用基矢生成一组倒矢之后，两个倒矢的长度分别是k1与k2的周期，每一组kx与ky的值可以用每一组k1与k2的值分别乘以两个单位倒矢，再进行矢量加法得到。这么做的好处是不同的模型只需要改哈密顿量以及基矢，计算陈数部分全部都统一了。”

这种方法其实挺不好理解的，没有前面两种直观。编程时需要注意：for循环是以k1和k2来取点，变换到kx和ky，取点的个数保持不变，但步长发生了变化。做了变换后，积分的个数和步长不是很统一。

根据文献中给的基矢（位置刚好对调），我画了示意图如下：

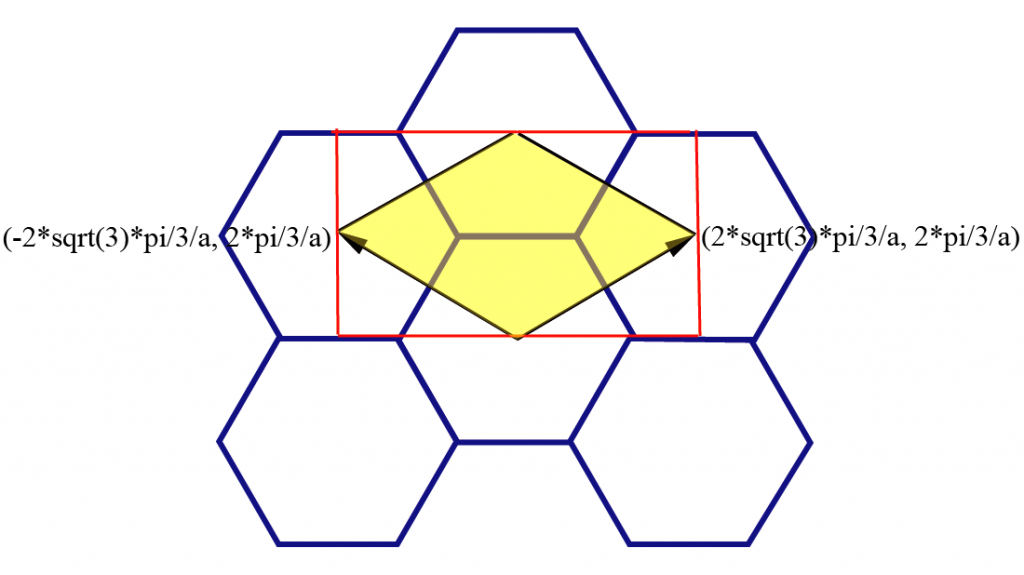
其中，基矢和基矢方向上某个长度为

$\overrightarrow{k_{10}}=(\frac{2\sqrt{3}\pi}{3a}, \frac{2\pi}{3a})$

$\overrightarrow{k_{20}}=(-\frac{2\sqrt{3}\pi}{3a}, \frac{2\pi}{3a})$

$k_{1}\overrightarrow{k_{10}}=(k_{1}\frac{2\sqrt{3}\pi}{3a}, k_{1}\frac{2\pi}{3a})$

$k_{2}\overrightarrow{k_{20}}=(-k_{2}\frac{2\sqrt{3}\pi}{3a}, k_{2}\frac{2\pi}{3a})$

因此， $k_x$ 和 $k_y$ 用基矢方向上的长度来表示为

$k_x=(k_{1}-k_{2})\frac{2\sqrt{3}\pi}{3a}$

$k_y=(k_{1}+k_{2})\frac{2\pi}{3a}$

需要注意的是坐标变换后，步长也要跟着一起变化，要保证步长与积分个数的乘积刚好为布里渊区面积，即S（布里渊区）=∫dkx*dky。

坐标变换前：

积分步长为：delta

积分个数：1/delta

坐标变换后：

令 bb1 = 2*sqrt(3)*pi/3/a 以及 bb2 = 2*pi/3/a

积分步长为：delta_x = delta*bb1*constant；delta_y= delta*bb2*constant

积分个数仍然是：1/delta

如果不包括积分函数项时，这里直接积分的结果是：bb1*bb2*constant*constant

当constant=1时，直接积分的面积是红色长方形的四份之一，是黄色布里渊区面积的二分之一。因此constant要取 $\sqrt{2}$ ，或者一个constant取2，一个constant取1。只要坐标变换后直接积分的结果是布里渊区的面积，步长不影响结果。尤其是当步长足够小时，在数值上没有太大区别。

代码如下：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/5133
"""

import numpy as np
import matplotlib.pyplot as plt
from math import *   # 引入pi, cos等
import cmath
import time
import functools  # 使用偏函数functools.partial()


def hamiltonian(k1, k2, M, t1, t2, phi, a=1/sqrt(3)):  # Haldane哈密顿量# Haldane哈密顿量（a为原子间距，不赋值的话默认为1/sqrt(3)）
    # 初始化为零矩阵
    h0 = np.zeros((2, 2), dtype=complex)
    h1 = np.zeros((2, 2), dtype=complex)
    h2 = np.zeros((2, 2), dtype=complex)

    # 质量项(mass term), 用于打开带隙
    h0[0, 0] = M
    h0[1, 1] = -M

    # 最近邻项
    h1[1, 0] = t1*(cmath.exp(1j*k2*a)+cmath.exp(1j*sqrt(3)/2*k1*a-1j/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j/2*k2*a))
    h1[0, 1] = h1[1, 0].conj()

    # # 最近邻项也可写成这种形式
    # h1[1, 0] = t1+t1*cmath.exp(1j*sqrt(3)/2*k1*a-1j*3/2*k2*a)+t1*cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a)
    # h1[0, 1] = h1[1, 0].conj()

    #次近邻项 # 对应陈数为-1
    h2[0, 0] = t2*cmath.exp(-1j*phi)*(cmath.exp(1j*sqrt(3)*k1*a)+cmath.exp(-1j*sqrt(3)/2*k1*a+1j*3/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a))
    h2[1, 1] = t2*cmath.exp(1j*phi)*(cmath.exp(1j*sqrt(3)*k1*a)+cmath.exp(-1j*sqrt(3)/2*k1*a+1j*3/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a))
    
    # # 次近邻项  # 对应陈数为1
    # h2[0, 0] = t2*cmath.exp(1j*phi)*(cmath.exp(1j*sqrt(3)*k1*a)+cmath.exp(-1j*sqrt(3)/2*k1*a+1j*3/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a))
    # h2[1, 1] = t2*cmath.exp(-1j*phi)*(cmath.exp(1j*sqrt(3)*k1*a)+cmath.exp(-1j*sqrt(3)/2*k1*a+1j*3/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a))

    matrix = h0 + h1 + h2 + h2.transpose().conj()
    return matrix


def main():
    start_clock = time.perf_counter()
    delta = 0.005
    chern_number = 0  # 陈数初始化
    
    # 常出现的项
    a = 1/sqrt(3)
    bb1 = 2*sqrt(3)*pi/3/a
    bb2 = 2*pi/3/a

    hamiltonian0 = functools.partial(hamiltonian, M=2/3, t1=1, t2=1/3, phi=pi/4, a=a)   # 使用偏函数，固定一些参数

    for k1 in np.arange(0 , 1, delta):
        print(k1)
        for k2 in np.arange(0, 1, delta):
            # 坐标变换
            kx = (k1-k2)*bb1
            ky = (k1+k2)*bb2

            # 这里乘2或除以2是为了保证“步长与积分个数的乘积刚好为布里渊区面积”
            delta_x = delta*bb1*2    
            delta_y = delta*bb2*2/2

            H = hamiltonian0(kx, ky) 
            eigenvalue, eigenvector = np.linalg.eig(H)
            vector = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 价带波函数
        
            H_delta_kx = hamiltonian0(kx+delta_x, ky) 
            eigenvalue, eigenvector = np.linalg.eig(H_delta_kx)
            vector_delta_kx = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]   # 略偏离kx的波函数

            H_delta_ky = hamiltonian0(kx, ky+delta_y)  
            eigenvalue, eigenvector = np.linalg.eig(H_delta_ky)
            vector_delta_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 略偏离ky的波函数
            
            H_delta_kx_ky = hamiltonian0(kx+delta_x, ky+delta_y)  
            eigenvalue, eigenvector = np.linalg.eig(H_delta_kx_ky)
            vector_delta_kx_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 略偏离kx和ky的波函数
            
            Ux = np.dot(np.conj(vector), vector_delta_kx)/abs(np.dot(np.conj(vector), vector_delta_kx))
            Uy = np.dot(np.conj(vector), vector_delta_ky)/abs(np.dot(np.conj(vector), vector_delta_ky))
            Ux_y = np.dot(np.conj(vector_delta_ky), vector_delta_kx_ky)/abs(np.dot(np.conj(vector_delta_ky), vector_delta_kx_ky))
            Uy_x = np.dot(np.conj(vector_delta_kx), vector_delta_kx_ky)/abs(np.dot(np.conj(vector_delta_kx), vector_delta_kx_ky))

            F = cmath.log(Ux*Uy_x*(1/Ux_y)*(1/Uy))
            # 陈数(chern number)
            chern_number = chern_number + F

    chern_number = chern_number/(2*pi*1j)
    print('Chern number = ', chern_number)
    end_clock = time.perf_counter()
    print('CPU执行时间(min)=', (end_clock-start_clock)/60)


if __name__ == '__main__':
    main()

计算结果为：

这里计算耗时会更少一些，可能的原因有：（1）没有if判断，节省计算时间；（2）经过变换后，可能是数值上恰好更容易收敛。

8,760 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】

Published by guanjihuan

View all posts by guanjihuan

43 thoughts on “Haldane模型中陈数的计算（附Python代码）”

li storm说道：

2023年11月28日 17:11

关老师，我能重复您石墨烯单带的数据但是用高效法（多能带）计算石墨烯超导时，只要加上例子空穴的部分，即使没用加超导，只是能带简并多了，也算不出正确的拓扑数。比如体内有gap，没有边界态，chern数应该为零。但是算出的为几百。

回复
1. guanjihuan说道：
  
  2023年11月28日 17:57
  
  有简并的情况参考这篇：陈数Chern number的计算（多条能带的高效法，附Python代码）。
  
  回复
匿名说道：

2023年10月26日 09:03

你好，如果更改最近邻与次近邻的强度，是否会影响布里渊区的大小？

回复
1. guanjihuan说道：
  
  2023年10月26日 22:11
  
  最近邻与次近邻的强度不影响布里渊区的大小。布里渊区的和元胞选取的大小以及晶格常数有关。
  
  回复
LYS说道：

2022年4月26日 16:53

你好，请问使用坐标变换方法，“这么做的好处是不同的模型只需要改哈密顿量以及基矢，计算陈数部分全部都统一了”这句话怎么理解？如何改哈密顿量以及基失？

回复
1. guanjihuan说道：
  
  2022年4月26日 18:32
  
  这句话不是我说的，大概可能是这样的意思：一般来说布里渊区是由基矢来决定，所以使用基矢量时，不管是什么模型，都可以用相同的方式积分，而不用适配于不同哈密顿量中不同形状的布里渊区。
  
  回复
  1. 匿名说道：
    
    2022年4月26日 19:07
    
    对于三角格子而言，布里渊区都是正六边形的。是不是所有的三角格子都可以这样积分，不需要管哈密顿量的具体形式（不同配置的三角格子哈密顿量不同，但布里渊区相似）
    
    回复
    1. guanjihuan说道：
      
      2022年4月27日 18:53
      
      嗯，总之要确保对布里渊区积分就行了，注意k的区间范围。
      
      回复
希夷说道：

2021年10月6日 16:44

非常感谢您的网页。
您的方法不太直观，而且有些步骤很绕。我把它做了另一个实现，欢迎围观。
https://zhuanlan.zhihu.com/p/416909597

回复
1. guanjihuan说道：
  
  2021年10月7日 21:46
  
  好的，关注了
  
  回复
匿名说道：

2021年7月29日 11:53

您好，我想问一个如果考虑磁子之间的相互作用，怎么把哈密顿量对角化来画色散关系呢

回复
1. guanjihuan说道：
  
  2021年7月29日 20:01
  
  不清楚，没考虑过，得看哈密顿量的具体形式吧。能带一般体现的是单体的性质，多体作用可能需要处理后才可以并入。
  
  回复
  1. 石墨烯条带陈数计算说道：
    
    2022年4月21日 10:15
    
    关老师，我现在计算石墨烯条带的陈数，因为考虑了边界效应，感觉计算陈数非常复杂，我没有理清楚思路，你能否给我介绍一下计算思路呢，万分感谢
    
    回复
    1. guanjihuan说道：
      
      2022年4月21日 11:40
      
      条带是没法算陈数的，因为陈数是bulk的性质，需要有kx和ky，维度为偶数维。如果需算了解石墨烯条带的拓扑性质，可以直接算二维石墨烯的陈数。石墨烯不考虑其他项时，陈数应该为零。
      还有一种是算实空间的陈数，那是另外一回事了。
      
      回复

博主这里只考虑了能带非简并情况，简并情况的代码如下，哈密顿量是一个kagome格子的：

%chen数高效法,布里渊区平移成矩形，简并陈数计算，算多条能带简并时，改的是函数M1、M2、u，有几个
%band_index就有几个u函数
function []=degen_chen_number_main2()
clear;clc
global delta band_index1 band_index2   band_index3   a
tic
delta = 0.01;
chern_number =0;  %陈数初始化
band_index1=1;%第几条能带索引？本征值最小的能带到本征值最大的能带，最大为矩阵阶数
band_index2=2;%简并带索引
band_index3=3;%简并带索引
%算某一能带的陈数可能在index中设置
% 几个坐标中常出现的项
%matlab的dot函数算复数似乎不是很好
a=1;
aa1=pi/a;
bb1=2*sqrt(3)*pi/(3*a);
ky0=0:delta:bb1;
kx0=0:delta:aa1;
temp1=length(kx0);
temp2=length(ky0);
for i=1:temp1
    i/temp1
    for j=1:temp2
        
            kx=kx0(i);ky=ky0(j);
            % 陈数(chern number)
            chern_number=chern_number + F(kx,ky);
        
    end
end
 
chern_number=chern_number/(2*pi*1j);
disp(['Chern number=',num2str(chern_number)])
toc
end

%%%%%%%%%%%%%%%%%%%%%%%%%

function [oput]=F(kx,ky)
global delta
oput=log(U1(kx,ky)*U2(kx+delta,ky)*(U1(kx, ky +delta)^(-1))*(U2(kx, ky)^(-1)));
end


function [op1]=U1(kx,ky)
op1=det(M1(kx,ky))/abs(det(M1(kx,ky)));
end

function [op2]=U2(kx,ky)
op2=det(M2(kx,ky))/abs(det(M2(kx,ky)));
end

function [o1]=M1(kx,ky)
global delta
o1=zeros(3);
o1(1,1)=u1(kx,ky)'*u1(kx + delta, ky);%u的排列和它的位置是有关的
o1(1,2)=u1(kx,ky)'*u2(kx + delta, ky);
o1(1,3)=u1(kx,ky)'*u3(kx + delta, ky);
o1(2,1)=u2(kx,ky)'*u1(kx + delta, ky);
o1(2,2)=u2(kx,ky)'*u2(kx + delta, ky);
o1(2,3)=u2(kx,ky)'*u3(kx + delta, ky);
o1(3,1)=u3(kx,ky)'*u1(kx + delta, ky);
o1(3,2)=u3(kx,ky)'*u2(kx + delta, ky);
o1(3,3)=u3(kx,ky)'*u3(kx + delta, ky);

end


function [o2]=M2(kx,ky)
global delta
o2=zeros(3);
o2(1,1)=u1(kx,ky)'*u1(kx , ky+ delta);
o2(1,2)=u1(kx,ky)'*u2(kx , ky+ delta);
o2(1,3)=u1(kx,ky)'*u3(kx , ky+ delta);
o2(2,1)=u2(kx,ky)'*u1(kx , ky+ delta);
o2(2,2)=u2(kx,ky)'*u2(kx , ky+ delta);
o2(2,3)=u2(kx,ky)'*u3(kx , ky+ delta);
o2(3,1)=u3(kx,ky)'*u1(kx , ky+ delta);
o2(3,2)=u3(kx,ky)'*u2(kx , ky+ delta);
o2(3,3)=u3(kx,ky)'*u3(kx , ky+ delta);

end


function [output]=u1(kx,ky)
global band_index1
getH=hamiltonian0(kx,ky);
[vector,value]=eig(getH);
[~,index]=sort(real(diag(value)));
output=vector(:,index(band_index1));%列向量
end

function [output]=u2(kx,ky)
global band_index2
getH=hamiltonian0(kx,ky);
[vector,value]=eig(getH);
[~,index]=sort(real(diag(value)));
output=vector(:,index(band_index2));%列向量
end

function [output]=u3(kx,ky)
global band_index3
getH=hamiltonian0(kx,ky);
[vector,value]=eig(getH);
[~,index]=sort(real(diag(value)));
output=vector(:,index(band_index3));%列向量
end

function [matrix]=hamiltonian0(kx, ky) %晶格常数a一般等于1
global a
phi=0;
t2=0;
t1=1;
 
a1=[-0.5,-sqrt(3)/2]*a;
a2=[1,0]*a;
a3=[-0.5,sqrt(3)/2]*a;
h1=zeros(3);
h2=zeros(3);

        k=[kx,ky];
        ezhen=exp(1i*phi/3);
        efu=exp(-1i*phi/3);
        c1=cos(k*a1');
        c2=cos(k*a2');
        c3=cos(k*a3');
        
        c32=cos(k*(a3-a2)');
        c21=cos(k*(a2-a1)');
        c31=cos(k*(a3-a1)');
        h1(1,2)=c1*efu;
        h1(2,1)=c1*ezhen;
        h1(1,3)=c3*ezhen;
        h1(3,1)=c3*efu;
        h1(2,3)=c2*efu;
        h1(3,2)=c2*ezhen;
        
        h1=h1*(-2*t1);%最终,最近临
        
        h2(1,2)=c32;
        h2(1,3)=c21;
        h2(2,1)=c32;
        h2(2,3)=c31;
        h2(3,1)=c21;
        h2(3,2)=c31;
        h2=h2*(-2*t2);%最终，次近临
        
       matrix=h1+h2;
 
end

guanjihuan说道：

2021年7月9日 19:11

嗯，感谢提供代码。问下：简并情况遇到的是什么问题？代码中需要修改和注意的是哪个地方？

回复
1. 匿名说道：
  
  2021年10月21日 10:20
  
  简并情况就是多个能带共用一个陈数
  
  回复
  1. 小王说道：
    
    2021年11月26日 13:25
    
    没有理解简并情况。。简并情况陈数还有好的定义吗
    
    回复
    1. guanjihuan说道：
      
      2021年11月27日 17:51
      
      如果能够区分开简并能带的波函数，然后就可以各自算陈数。在数值计算过程中可能会存在一些问题，比如每个k点得到的简并能带的波函数完全不同，需要额外的代码进行变换处理。
      
      此外，在数值上还有一种方法是加个极小的微扰使得能带退简并，这种方法比较简单，缺点是可能会略微破坏原本的对称性。如果对称性对整个体系的性质没太大影响，可以这么做。
      
      应该有更好的算法来计算简并的情况，有需要可以查些文献看看。我之后可能也会考虑下。
      
      回复
    2. 匿名说道：
      
      2021年12月30日 11:46
      
      简并陈数并不是什么新奇的概念，相关文献很多
      
      回复
li说道：

2022年4月24日 21:50

您好，我有一个问题，就是对于二阶简并陈数，是否可以先用这个程序算出F_xy,F_zw, F_xz,.....代入二阶陈数表达式中？

回复

匿名说道：

2021年6月23日 16:57

这个似乎都是非简并陈数的算法，简并陈数的算法没有写进去吗？

回复
1. guanjihuan说道：
  
  2021年6月23日 20:15
  
  嗯，这里没考虑简并的情况。
  
  回复

我把积分方法1的python代码改成了matlab的，但是算的陈数是几百，不知道错在哪里了，哪位大神可以帮忙看下错在哪？

function []=chen_number_main()
    tic
    delta = 0.005;
    chern_number = 0;  %陈数初始化
    
    % 几个坐标中常出现的项
    a = 1/sqrt(3);
    aa1 = 4*sqrt(3)*pi/9/a;
    aa2 = 2*sqrt(3)*pi/9/a;
    bb1 = 2*pi/3/a;

   
    for kx =-aa1:delta:aa1%in np.arange(-aa1, aa1, delta):
        kx
        for ky=-bb1:delta:bb1%in np.arange(-bb1, bb1, delta):
            if (-aa2<=kxaa2 && -(aa1-kx)*tan(pi/3)<=ky<=(aa1-kx)*tan(pi/3))...
                || (kx<-aa2 && -(kx-(-aa1))*tan(pi/3)<=ky<=(kx-(-aa1))*tan(pi/3))  % 限制在六角格子布里渊区内

                H=hamiltonian0(kx, ky); 
                [eigenvector,eigenvalue]=eig(H);
                [~,index]=sort(real(eigenvalue));
                vector = eigenvector(:,index(1));%价带波函数,本征值最小的点对应的波函数列向量
               
                
                H_delta_kx=hamiltonian0(kx+delta, ky); 
                [eigenvector, eigenvalue]=eig(H_delta_kx);
                [~,index]=sort(real(eigenvalue));
                vector_delta_kx=eigenvector(:,index(1));   % 略偏离kx的波函数

                H_delta_ky=hamiltonian0(kx, ky+delta);  
                [eigenvector, eigenvalue]=eig(H_delta_ky);
                [~,index]=sort(real(eigenvalue));
                vector_delta_ky=eigenvector(:,index(1));  % 略偏离ky的波函数
                
                H_delta_kx_ky=hamiltonian0(kx+delta, ky+delta);  
               [eigenvector, eigenvalue]=eig(H_delta_kx_ky);
               [~,index]=sort(real(eigenvalue));
               vector_delta_kx_ky=eigenvector(:,index(1));  %略偏离kx和ky的波函数
                
                Ux=dot(conj(vector),vector_delta_kx)./abs(dot(conj(vector),...
                                                                         vector_delta_kx));
                Uy=dot(conj(vector),vector_delta_ky)./abs(dot(conj(vector),...
                                                                         vector_delta_ky));
                Ux_y=dot(conj(vector_delta_ky),vector_delta_kx_ky)./abs(...
                dot(conj(vector_delta_ky),vector_delta_kx_ky));
                Uy_x=dot(conj(vector_delta_kx),vector_delta_kx_ky)./abs(...
                dot(conj(vector_delta_kx),vector_delta_kx_ky));

                F = log(Ux.*Uy_x.*(1/Ux_y).*(1/Uy));

                % 陈数(chern number)
                chern_number=chern_number + F;
            end
        end
    end
    
    chern_number=chern_number/(2*pi*1j);
    disp(['Chern number=',num2str(chern_number)])
    toc
end


function [out]=hamiltonian0(kx,ky)
out=hamiltonian(kx, ky, 2/3, 1, 1/3, pi/4, 1/sqrt(3));
end


function [matrix]=hamiltonian(k1, k2, M, t1, t2, phi, a) %Haldane哈密顿量(a为原子间距，不赋值的话默认为1/sqrt(3)）
  
    h0 = zeros(2,2);  
    h2 = zeros(2,2);

   % 质量项(mass term), 用于打开带隙
    h0(1,1) = M;
    h0(2,2)= -M;

   %最近邻项
    h1(2,1) = t1*(exp(1j*k2*a)+...
    exp(1j*(sqrt(3)/2)*k1*a-(1j/2)*k2*a)+exp(-1j*(sqrt(3)/2)*k1*a-(1j/2)*k2*a));
    h1(1,2) = conj(h1(2,1));

    %次近邻项 # 对应陈数为-1
    h2(1,1) = t2*exp(-1j*phi)*(exp(1j*sqrt(3)*k1*a)+...
    exp(-1j*(sqrt(3)/2)*k1*a+1j*3/2*k2*a)+exp(-1j*(sqrt(3)/2)*k1*a-1j*(3/2)*k2*a));
    h2(2,2) = t2*exp(1j*phi)*(exp(1j*sqrt(3)*k1*a)+...
    exp(-1j*(sqrt(3)/2)*k1*a+1j*(3/2)*k2*a)+exp(-1j*(sqrt(3)/2)*k1*a-1j*(3/2)*k2*a));
    
    % 次近邻项  # 对应陈数为1
   % h2[0, 0] = t2*cmath.exp(1j*phi)*(cmath.exp(1j*sqrt(3)*k1*a)+cmath.exp(-1j*sqrt(3)/2*k1*a+1j*3/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a))
    %h2[1, 1] = t2*cmath.exp(-1j*phi)*(cmath.exp(1j*sqrt(3)*k1*a)+cmath.exp(-1j*sqrt(3)/2*k1*a+1j*3/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a))

    matrix = h0 + h1 + h2 + h2';
    
end

匿名说道：

2021年6月10日 21:02

可以复制到matlab里看一下

回复

如果是一一对应的，应该不会有太大问题。你可以关闭循环，以某个值代替，然后在某个语句前后都分别输出数值结果，一步步对比验证，找到导致数值不一样的语句，就是出错的地方。

修改好的matlab代码，可以运行，速度较python快了很多，方法1：

function []=chen_number_main()
clear;clc
tic
delta = 0.005;
chern_number = 0;  %陈数初始化
%算某一能带的陈数可能在index中设置
% 几个坐标中常出现的项
%matlab的dot函数算复数似乎不是很好
a = 1/sqrt(3);
aa1 = 4*sqrt(3)*pi/9/a;
aa2 = 2*sqrt(3)*pi/9/a;
bb1 = 2*pi/3/a;
ky0=-bb1:delta:bb1;
kx0=-aa1:delta:aa1;
temp1=length(kx0);
temp2=length(ky0);
for i=1:temp1
    kx0(i)
    for j=1:temp2
        if abs(kx0(i))<=aa2+tand(30)*(bb1-abs(ky0(j)))  % 限制在六角格子布里渊区内,只适用于正六角格子,新的限制算法，ref：https://blog.csdn.net/cuixiping/article/details/11716805?utm_medium=distribute.pc_relevant.none-task-blog-baidujs_title-0&spm=1001.2101.3001.4242
            kx=kx0(i);ky=ky0(j);
            H=hamiltonian0(kx, ky);
            [eigenvector,eigenvalue]=eig(H);
            [~,index]=sort(real(diag(eigenvalue)));
            vector = eigenvector(:,index(1));%价带波函数,本征值最小的点对应的波函数列向量
            
            
            H_delta_kx=hamiltonian0(kx+delta, ky);
            [eigenvector, eigenvalue]=eig(H_delta_kx);
            [~,index]=sort(real(diag(eigenvalue)));
            vector_delta_kx=eigenvector(:,index(1));   % 略偏离kx的波函数
            
            H_delta_ky=hamiltonian0(kx, ky+delta);
            [eigenvector, eigenvalue]=eig(H_delta_ky);
            [~,index]=sort(real(diag(eigenvalue)));
            vector_delta_ky=eigenvector(:,index(1));  % 略偏离ky的波函数
            
            H_delta_kx_ky=hamiltonian0(kx+delta, ky+delta);
            [eigenvector, eigenvalue]=eig(H_delta_kx_ky);
            [~,index]=sort(real(diag(eigenvalue)));
            vector_delta_kx_ky=eigenvector(:,index(1));  %略偏离kx和ky的波函数
            
            
            Ux=(vector'*vector_delta_kx)./abs((vector'*vector_delta_kx));
            Uy=(vector'*vector_delta_ky)./abs((vector'*vector_delta_ky));
            Ux_y=(vector_delta_ky'*vector_delta_kx_ky)./abs((vector_delta_ky'*vector_delta_kx_ky));
            Uy_x=(vector_delta_kx'*vector_delta_kx_ky)./abs((vector_delta_kx'*vector_delta_kx_ky));
            
            
            F = log(Ux.*Uy_x.*(1/Ux_y).*(1/Uy));
            
            % 陈数(chern number)
            chern_number=chern_number + F;
        end
    end
end

chern_number=chern_number/(2*pi*1j);
disp(['Chern number=',num2str(chern_number)])
toc
end


function [out]=hamiltonian0(kx,ky)
out=hamiltonian(kx, ky, 2/3, 1, 1/3, pi/4, 1/sqrt(3));
end


function [matrix]=hamiltonian(k1, k2, M, t1, t2, phi, a) %Haldane哈密顿量(a为原子间距，不赋值的话默认为1/sqrt(3)）

h0 = zeros(2,2);
h2 = zeros(2,2);

% 质量项(mass term), 用于打开带隙
h0(1,1) = M;
h0(2,2)= -M;

%最近邻项
h1(2,1) = t1*(exp(1j*k2*a)+...
    exp(1j*(sqrt(3)/2)*k1*a-(1j/2)*k2*a)+exp(-1j*(sqrt(3)/2)*k1*a-(1j/2)*k2*a));
h1(1,2) = conj(h1(2,1));

%次近邻项 # 对应陈数为-1
h2(1,1) = t2*exp(-1j*phi)*(exp(1j*sqrt(3)*k1*a)+...
    exp(-1j*(sqrt(3)/2)*k1*a+1j*3/2*k2*a)+exp(-1j*(sqrt(3)/2)*k1*a-1j*(3/2)*k2*a));
h2(2,2) = t2*exp(1j*phi)*(exp(1j*sqrt(3)*k1*a)+...
    exp(-1j*(sqrt(3)/2)*k1*a+1j*(3/2)*k2*a)+exp(-1j*(sqrt(3)/2)*k1*a-1j*(3/2)*k2*a));

% 次近邻项  # 对应陈数为1
% h2[0, 0] = t2*cmath.exp(1j*phi)*(cmath.exp(1j*sqrt(3)*k1*a)+cmath.exp(-1j*sqrt(3)/2*k1*a+1j*3/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a))
%h2[1, 1] = t2*cmath.exp(-1j*phi)*(cmath.exp(1j*sqrt(3)*k1*a)+cmath.exp(-1j*sqrt(3)/2*k1*a+1j*3/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a))

matrix = h0 + h1 + h2 + h2';

end

guanjihuan说道：

2021年6月11日 19:50

嗯，在有一些情况下（比如可能是循环），Matlab会比Python快很多。我之所以不怎么爱用Matlab，是因为不是开源的，而且软件安装比较麻烦，体积太大。如果追求运行效率，我一般会用Fortran或者C语言。

回复
1. 匿名说道：
  
  2021年6月14日 16:01
  
  限制在六边形的算法改了
  
  回复
  1. guanjihuan说道：
    
    2021年6月15日 08:54
    
    嗯，都可以的
    
    回复
    1. 匿名说道：
      
      2021年12月27日 21:37
      
      我又弄了新的更简洁的限制在六边形布里渊区内的代码，如下：
      function [out]=shape_f(xx,yy,xp,yp)
      %xx、yy是输入的要判断的点，
      %xp 、yp是多边形的顶点(顺时针或逆时针，首尾相连)
      %xp、yp是向量
      %如果在多边形内或边上，out为1，否则为0
      out=double(inpolygon(xx,yy,xp,yp));
      
      end
      
      回复
      1. guanjihuan说道：
        
        2021年12月28日 13:49
        
        嗯，都是可以的。我这里的代码也没有做过多的优化，只是作为例子实现对应的功能。此外，这个对运行速度的影响应该不是很大。

灰色XT说道：

2020年12月8日 14:18

# 这里乘2或除以2是为了保证“步长与积分个数的乘积刚好为布里渊区面积”
delta_x = delta*bb1*2
delta_y = delta*bb2*2/2

这个地方的delta_x,y根据文中说法不应该是在bb1,2后面成以sqrt(2)吗？
所以是不是手误打错了？

回复
1. guanjihuan说道：
  
  2020年12月8日 14:52
  
  不算是错的，两种都可以。constant取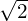 $\sqrt{2}$ ，或者一个constant取2，一个constant取1。只要坐标变换后直接积分的结果是布里渊区的面积，步长的选取不影响结果。尤其是当步长足够小时，在数值上没有太大区别。（在博文中也添加这个评论）
  
  回复
LHC说道：

2020年11月25日 17:12

博主你好

不同于这篇文章的陈数，请问博主接触过高阶拓扑绝缘体的拓扑不变量（Bulk Polarization）吗？

例如计算出kagome模型的陈数是变化的，但是其Bulk Polarization就是 (1/3, 1/3) ，近期一直尝试计算，可是一直一直出错。。。：(

https://zhuanlan.zhihu.com/p/175953375

回复
1. guanjihuan说道：
  
  2020年11月26日 19:57
  
  我目前还没怎么接触高阶拓扑绝缘体的拓扑不变量，之后可能也会考虑。你可以多看些文献，确保对该不变量的理解是正确的，或者用简单体系做一下测试，找找程序的问题。
  
  回复
  1. LHC说道：
    
    2020年11月27日 08:54
    
    ok,谢谢博主
    
    回复
Zhuof说道：

2020年9月21日 17:38

您好，感谢分享。我觉得你这里程序中的“a = 1/sqrt(3)”是错误的，应该是"a=1"，如果a是 carbon-carbon distance的话。可以参考review “The electronic properties of graphene”。

回复
1. guanjihuan说道：
  
  2020年9月21日 21:44
  
  不影响的，a可以取任何相对的值，对应的布里渊区大小会有变化。在博文中我是取次近邻原子间的距离为1，所以a = 1/sqrt(3)。如果a取为1也是可以的。
  
  回复
  1. Zhuof说道：
    
    2020年9月22日 09:23
    
    嗯，我没注意看你的哈密顿量。
    
    回复

我用你的“陈数Chern number的计算（定义法）（附Python、Matlab代码）”博文里面提到的matlab代码，并且结合你在“Haldane模型哈密顿量与能带图（附Python代码）”博文开头提到的Haldane模型的哈密顿量（含泡利矩阵那个），选取原子间距为1时，得到陈数为2.8690，原子间距为1/sqrt(3)时得到陈数为0.6313（m=2/3，t1=1,t2=2/3,phi=0.25pi），一直想不通哪里出了问题，回到你现在这篇博文的代码里发现你这里的哈密顿量好像有一点点不一样...

matlab代码（a=1）：

%陈数定义法
clear;clc;
n=100;%积分密度
delta=1e-5;%求导的偏离量
C=0;%陈数初始化
for kx=-pi:(1/n):pi
    for ky=-pi:(1/n):pi
        VV=get_vector(HH(kx,ky));
        Vkx=get_vector(HH(kx+delta,ky));%略偏离kx的波函数
        Vky=get_vector(HH(kx,ky+delta));%略偏离ky的波函数
        Vkxky=get_vector(HH(kx+delta,ky+delta));%略偏离kx，ky的波函数
        if  sum((abs(Vkx-VV)))>0.01   %为了波函数的连续性（这里的不连续只遇到符号问题，所以可以直接这么处理）
            Vkx=-Vkx;
        end
        
        if  sum((abs(Vky-VV)))>0.01
            Vky=-Vky;
        end
        
        if  sum(abs(Vkxky-VV))>0.01
            Vkxky=-Vkxky;
        end
        %价带的波函数的berry connection，求导后内积
        Ax=VV'*(Vkx-VV)/delta;%Berry connection Ax
        Ay=VV'*(Vky-VV)/delta;%Berry connection Ay
        Ax_delta_ky=Vky'*(Vkxky-Vky)/delta;%略偏离ky的berry connection Ax
        Ay_delta_kx=Vkx'*(Vkxky-Vkx)/delta;%略偏离kx的berry connection Ay
        %berry curvature
        F=((Ay_delta_kx-Ay)-(Ax_delta_ky-Ax))/delta;
        %chern number
        C=C+F*(1/n)^2;  
    end
end
C=C/(2*pi*1i)


function vector_new = get_vector(H)
[vector,eigenvalue] = eig(H);
[eigenvalue, index]=sort(diag(eigenvalue), 'descend');
vector_new = vector(:, index(2));
end

function H=HH(kx,ky)
H(1,1)=-2*1/3*cos(0.25*pi).*(cos(sqrt(3)*1*kx)+cos(-0.5*sqrt(3)*1*kx+3/2*1*ky)+cos(0.5*sqrt(3)*1*kx+3/2*1*ky))+2/3+2*1/3*sin(0.25*pi).*(sin(sqrt(3)*1*kx)+sin(-0.5*sqrt(3)*1*kx+3/2*1*ky)+sin(-0.5*sqrt(3)*1*kx-3/2*1*ky));
H(1,2)=-1*(cos(1*ky)+cos(-0.5*sqrt(3)*1*kx-0.5*1*ky)+cos(0.5*sqrt(3)*1*kx-0.5*1*ky))-1i*(1*(sin(1*ky)+sin(-0.5*sqrt(3)*1*kx-0.5*1*ky)+sin(0.5*sqrt(3)*1*kx-0.5*1*ky)));
H(2,1)=-1*(cos(1*ky)+cos(-0.5*sqrt(3)*1*kx-0.5*1*ky)+cos(0.5*sqrt(3)*1*kx-0.5*1*ky))+1i*(1*(sin(1*ky)+sin(-0.5*sqrt(3)*1*kx-0.5*1*ky)+sin(0.5*sqrt(3)*1*kx-0.5*1*ky)));
H(2,2)=-2*1/3*cos(0.25*pi).*(cos(sqrt(3)*1*kx)+cos(-0.5*sqrt(3)*1*kx+3/2*1*ky)+cos(0.5*sqrt(3)*1*kx+3/2*1*ky))-(2/3+2*1/3*sin(0.25*pi).*(sin(sqrt(3)*1*kx)+sin(-0.5*sqrt(3)*1*kx+3/2*1*ky)+sin(-0.5*sqrt(3)*1*kx-3/2*1*ky)));
end

然后我就去按照你有关python博文里面搞了一下python，把我上面matlab代码里面的哈密顿量化简后替代现在这篇博文里面代码的哈密顿量，得到
chern number=1.0000000000000133+2.363979843223985e-13j

python代码：

import numpy as np
import matplotlib.pyplot as plt
from math import *   # 引入pi, cos等
import cmath
import time
import functools  # 使用偏函数functools.partial()


def hamiltonian(k1, k2, M, t1, t2, phi, a=1):  # Haldane哈密顿量(a为原子间距，不赋值的话默认为1/sqrt(3)）
    # 初始化为零矩阵
    h0 = np.zeros((2, 2))*(1+0j)   # 乘(1+0j)是为了把h0转为复数
    h1 = np.zeros((2, 2))*(1+0j)
    h2 = np.zeros((2, 2))*(1+0j)

    # 质量项(mass term), 用于打开带隙
    h0[0, 0] = M
    h0[1, 1] = -M

    # 最近邻项
#     h1[1, 0] = t1*(cmath.exp(1j*k2*a)+cmath.exp(1j*sqrt(3)/2*k1*a-1j/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j/2*k2*a))
#     h1[0, 1] = h1[1, 0].conj()
    h1[1, 0] = t1*(cmath.exp(1j*k2*a)+2*cmath.cos(0.5*sqrt(3)*k1*a)*cmath.exp(-1j*0.5*k2*a))
    h1[0, 1] = t1*(cmath.exp(-1j*k2*a)+2*cmath.cos(0.5*sqrt(3)*k1*a)*cmath.exp(1j*0.5*k2*a))
    #次近邻项 # 对应陈数为-1
#     h2[0, 0] = t2*cmath.exp(-1j*phi)*(cmath.exp(1j*sqrt(3)*k1*a)+cmath.exp(-1j*sqrt(3)/2*k1*a+1j*3/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a))
#     h2[1, 1] = t2*cmath.exp(1j*phi)*(cmath.exp(1j*sqrt(3)*k1*a)+cmath.exp(-1j*sqrt(3)/2*k1*a+1j*3/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a))
    h2[0, 0] = -2*t2*(-cmath.cos(phi+sqrt(3)*k1*a)-2*cmath.cos(3/2*k2*a)*cmath.cos(phi-0.5*sqrt(3)*k1*a))
    h2[1, 1] = 2*t2*(cmath.cos(phi-sqrt(3)*k1*a)+2*cmath.cos(3/2*k2*a)*cmath.cos(phi+0.5*sqrt(3)*k1*a))
    
    # # 次近邻项  # 对应陈数为1
    # h2[0, 0] = t2*cmath.exp(1j*phi)*(cmath.exp(1j*sqrt(3)*k1*a)+cmath.exp(-1j*sqrt(3)/2*k1*a+1j*3/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a))
    # h2[1, 1] = t2*cmath.exp(-1j*phi)*(cmath.exp(1j*sqrt(3)*k1*a)+cmath.exp(-1j*sqrt(3)/2*k1*a+1j*3/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a))

    matrix = h0 + h1 + h2
    return matrix


def main():
    start_clock = time.perf_counter()
    delta = 0.002
    chern_number = 0  # 陈数初始化
    
    # 常出现的项
    a = 1
    bb1 = 2*sqrt(3)*pi/3/a
    bb2 = 2*pi/3/a

    hamiltonian0 = functools.partial(hamiltonian, M=2/3, t1=1, t2=1/3, phi=pi/4, a=a)   # 使用偏函数，固定一些参数

    for k1 in np.arange(0 , 1, delta):
        print(k1)
        for k2 in np.arange(0, 1, delta):
            # 坐标变换
            kx = (k1-k2)*bb1
            ky = (k1+k2)*bb2

            # 这里乘2或除以2是为了保证“步长与积分个数的乘积刚好为布里渊区面积”
            delta_x = delta*bb1*2    
            delta_y = delta*bb2*2/2

            H = hamiltonian0(kx, ky) 
            eigenvalue, eigenvector = np.linalg.eig(H)
            vector = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 价带波函数
        
            H_delta_kx = hamiltonian0(kx+delta_x, ky) 
            eigenvalue, eigenvector = np.linalg.eig(H_delta_kx)
            vector_delta_kx = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]   # 略偏离kx的波函数

            H_delta_ky = hamiltonian0(kx, ky+delta_y)  
            eigenvalue, eigenvector = np.linalg.eig(H_delta_ky)
            vector_delta_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 略偏离ky的波函数
            
            H_delta_kx_ky = hamiltonian0(kx+delta_x, ky+delta_y)  
            eigenvalue, eigenvector = np.linalg.eig(H_delta_kx_ky)
            vector_delta_kx_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 略偏离kx和ky的波函数
            
            Ux = np.dot(np.conj(vector), vector_delta_kx)/abs(np.dot(np.conj(vector), vector_delta_kx))
            Uy = np.dot(np.conj(vector), vector_delta_ky)/abs(np.dot(np.conj(vector), vector_delta_ky))
            Ux_y = np.dot(np.conj(vector_delta_ky), vector_delta_kx_ky)/abs(np.dot(np.conj(vector_delta_ky), vector_delta_kx_ky))
            Uy_x = np.dot(np.conj(vector_delta_kx), vector_delta_kx_ky)/abs(np.dot(np.conj(vector_delta_kx), vector_delta_kx_ky))

            F = cmath.log(Ux*Uy_x*(1/Ux_y)*(1/Uy))
            # 陈数(chern number)
            chern_number = chern_number + F

    chern_number = chern_number/(2*pi*1j)
    print('Chern number = ', chern_number)
    end_clock = time.perf_counter()
    print('CPU执行时间(min)=', (end_clock-start_clock)/60)


if __name__ == '__main__':
    main()

嗯...可能那篇博文给的matlab代码算法上不适合算蜂窝格子吧...
对我帮助很大，非常感谢！！！

guanjihuan说道：

2020年7月21日 23:58

你前面matlab代码遇到的问题是因为你积分没有限制在布里渊区内。六角格子的布里渊区还是六角格子，已经不能在[-pi, pi]*[-pi, pi]区域积分了。有两种处理办法，一个是用条件语句把积分限制在布里渊区，还有一个办法是坐标变换。本篇列出的就是这两种处理办法。

此外，也尽量少用定义的方法吧。定义法可以作为入门，比较直观，但在计算中经常会遇到波函数不连续的问题。这里是2乘2的矩阵，波函数还不会遇到麻烦，而对于矩阵比较大的矩阵时，求解时波函数的连续性会比较难处理。

回复
1. lhc说道：
  
  2020年7月22日 16:57
  
  嗯嗯，感谢~~
  
  回复

一、积分方法1：限制积分范围在六角晶格内

二、积分方法2：布里渊区平移成方形

三、积分方法3：坐标变换

Published by guanjihuan

43 thoughts on “Haldane模型中陈数的计算（附Python代码）”

发表评论 取消回复

发表评论取消回复