在量子力学中,经常会遇到矩阵两侧乘上向量或者泡利矩阵,这里给出乘积后展开的形式,以便之后在阅读文献时,可以了解到中间被省略的推导过程。
假设矩阵为:
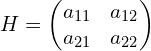
1. 矩阵两边乘上向量
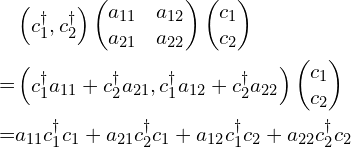
在最后的表达式中可以看到矩阵上的元素和向量中元素的对应关系。在文献中,哈密顿量一般会写成这两种形式:一个是矩阵的形式,一个是展开的形式。
2. 矩阵两边乘上泡利矩阵
矩阵两边乘上泡利矩阵一般会在幺正变换中出现,这包括哈密顿量满足某种对称性的情况。
(1)两边乘上![]()
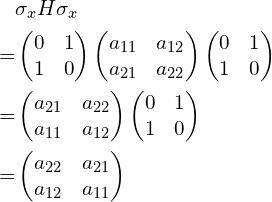
可以看到结果为:矩阵对角线的两个元素互换,非对角线的两个元素互换。
(2)两边乘上![]()
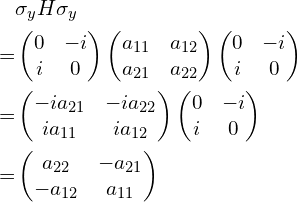
可以看到结果为:矩阵对角线的两个元素互换,非对角线的两个元素互换并且加上一个负号。
(3)两边乘上![]()
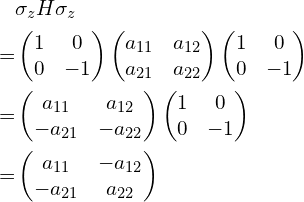
可以看到结果为:矩阵的元素位置都没有变,非对角线的两个元素加上一个负号。
综上,还可以发现![]() 和
和![]() 的联合作用效果等同于
的联合作用效果等同于![]() 的作用效果,这是因为
的作用效果,这是因为
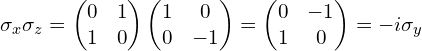
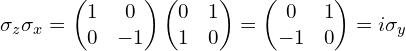
所以有
![]()
关于泡利矩阵的张量积(不是乘积),阅读博文:泡利矩阵以及泡利矩阵的张量积。
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】