Kane-Mele模型的哈密顿量和能带图（不考虑Rashba自旋轨道耦合的情况，附Python/Matlab代码）

Kane-Mele模型原始论文为：Z2 Topological Order and the Quantum Spin Hall Effect、Quantum Spin Hall Effect in Graphene。

这里考虑没有Rashba自旋轨道耦合的情况，哈密顿量为：

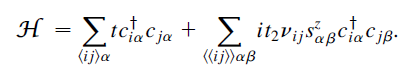
此时的哈密顿量可以分解成两个独立的Haldane模型。Haldane模型可以参考这篇：Haldane模型哈密顿量与能带图（附Python代码）。

自旋向上和自旋向下对应的Haldane模型给出相反的霍尔电导，整体满足时间反演对称性。

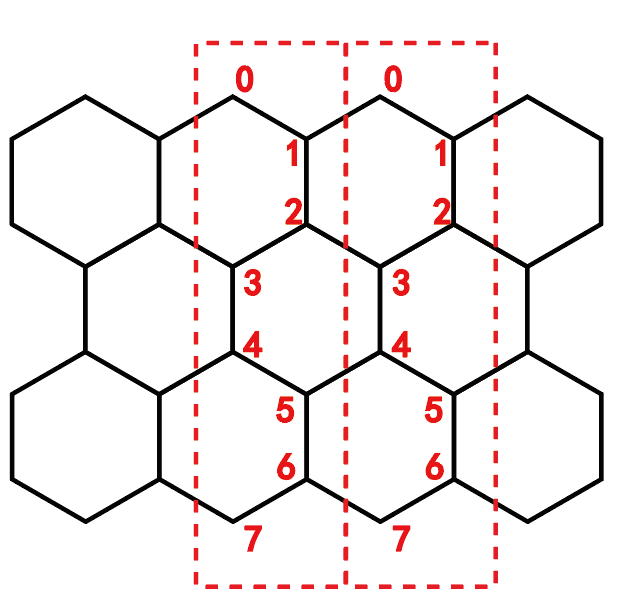
蜂窝格子的编号为：

准一维的Kane-Mele模型（不考虑Rashba自旋轨道耦合）能带图代码为：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/4829
"""

import numpy as np
import matplotlib.pyplot as plt
from math import * 
import cmath 
import functools


def hamiltonian(k, N, M, t1, t2, phi):  # Kane-Mele model
    # 初始化为零矩阵
    h00 = np.zeros((2*4*N, 2*4*N), dtype=complex) # 因为自旋有上有下，所以整个维度要乘2。这里4是元胞内部重复单位的大小，规定元胞大小以4来倍增。
    h01 = np.zeros((2*4*N, 2*4*N), dtype=complex)

    for spin in range(2):
        # 原胞内的跃迁h00
        for i in range(N):
            # 最近邻
            h00[i*4*2+0*2+spin, i*4*2+1*2+spin] = t1 
            h00[i*4*2+1*2+spin, i*4*2+0*2+spin] = t1

            h00[i*4*2+1*2+spin, i*4*2+2*2+spin] = t1  
            h00[i*4*2+2*2+spin, i*4*2+1*2+spin] = t1

            h00[i*4*2+2*2+spin, i*4*2+3*2+spin] = t1  
            h00[i*4*2+3*2+spin, i*4*2+2*2+spin] = t1

            # 次近邻
            h00[i*4*2+0*2+spin, i*4*2+2*2+spin] = t2*cmath.exp(-1j*phi)*sign_spin(spin)    
            h00[i*4*2+2*2+spin, i*4*2+0*2+spin] = h00[i*4*2+0*2+spin, i*4*2+2*2+spin].conj()
            h00[i*4*2+1*2+spin, i*4*2+3*2+spin] = t2*cmath.exp(-1j*phi)*sign_spin(spin) 
            h00[i*4*2+3*2+spin, i*4*2+1*2+spin] = h00[i*4*2+1*2+spin, i*4*2+3*2+spin].conj()
            
        for i in range(N-1):
            # 最近邻
            h00[i*4*2+3*2+spin, (i+1)*4*2+0*2+spin] = t1  
            h00[(i+1)*4*2+0*2+spin, i*4*2+3*2+spin] = t1

            # 次近邻
            h00[i*4*2+2*2+spin, (i+1)*4*2+0*2+spin] = t2*cmath.exp(1j*phi)*sign_spin(spin) 
            h00[(i+1)*4*2+0*2+spin, i*4*2+2*2+spin] = h00[i*4*2+2*2+spin, (i+1)*4*2+0*2+spin].conj()
            h00[i*4*2+3*2+spin, (i+1)*4*2+1*2+spin] = t2*cmath.exp(1j*phi)*sign_spin(spin) 
            h00[(i+1)*4*2+1*2+spin, i*4*2+3*2+spin] = h00[i*4*2+3*2+spin, (i+1)*4*2+1*2+spin].conj()

        # 原胞间的跃迁h01
        for i in range(N):
            # 最近邻
            h01[i*4*2+1*2+spin, i*4*2+0*2+spin] = t1  
            h01[i*4*2+2*2+spin, i*4*2+3*2+spin] = t1

            # 次近邻
            h01[i*4*2+0*2+spin, i*4*2+0*2+spin] = t2*cmath.exp(1j*phi)*sign_spin(spin)  
            h01[i*4*2+1*2+spin, i*4*2+1*2+spin] = t2*cmath.exp(-1j*phi)*sign_spin(spin) 
            h01[i*4*2+2*2+spin, i*4*2+2*2+spin] = t2*cmath.exp(1j*phi)*sign_spin(spin) 
            h01[i*4*2+3*2+spin, i*4*2+3*2+spin] = t2*cmath.exp(-1j*phi)*sign_spin(spin) 

            h01[i*4*2+1*2+spin, i*4*2+3*2+spin] = t2*cmath.exp(1j*phi)*sign_spin(spin)  
            h01[i*4*2+2*2+spin, i*4*2+0*2+spin] = t2*cmath.exp(-1j*phi)*sign_spin(spin) 

            if i != 0:
                h01[i*4*2+1*2+spin, (i-1)*4*2+3*2+spin] = t2*cmath.exp(1j*phi)*sign_spin(spin)   
                
        for i in range(N-1):
            h01[i*4*2+2*2+spin, (i+1)*4*2+0*2+spin] = t2*cmath.exp(-1j*phi)*sign_spin(spin) 

    matrix = h00 + h01*cmath.exp(1j*k) + h01.transpose().conj()*cmath.exp(-1j*k)
    return matrix


def sign_spin(spin):
    if spin==0:
        sign=1
    else:
        sign=-1
    return sign


def main():
    hamiltonian0 = functools.partial(hamiltonian, N=20, M=0, t1=1, t2=0.03, phi=pi/2)
    k = np.linspace(0, 2*pi, 300)
    plot_bands_one_dimension(k, hamiltonian0)


def plot_bands_one_dimension(k, hamiltonian):
    dim = hamiltonian(0).shape[0]
    dim_k = k.shape[0]
    eigenvalue_k = np.zeros((dim_k, dim)) 
    i0 = 0
    for k0 in k:
        matrix0 = hamiltonian(k0)
        eigenvalue, eigenvector = np.linalg.eig(matrix0)
        eigenvalue_k[i0, :] = np.sort(np.real(eigenvalue[:]))
        i0 += 1
    for dim0 in range(dim):
        plt.plot(k, eigenvalue_k[:, dim0], '-k')  
    plt.ylim(-1, 1)
    plt.show()


if __name__ == '__main__': 
    main()

计算出的能带图为：

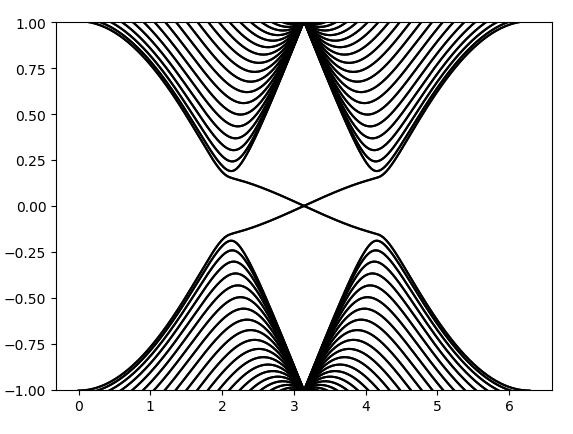
这里画出来的能带和Haldane模型对应参数的能带看起来完全一样，但这里的能带是二重简并的，且有不同的拓扑性质。这里的拓扑性质由Z2不变量来定义。

关于详细的讨论以及考虑Rashba自旋轨道耦合的情况，可以看原始论文或者相关综述。

实验上首先发现该量子自旋霍尔效应的是在Mercury Telluride Quantum Wells中，该体系由BHZ模型来描述，参考这篇：BHZ模型哈密顿量与能带图（附Python代码）。

附Matlab代码（由Zhong-Fu Li同学提供）：

% Purpose: Plot Kane-Mele's bands
% Date: Dec 07, 2021 @HNU
% Author: Ji-Huan Guan; 
% Modify by Zhong-Fu Li;
% More code can be found in https://www.guanjihuan.com/

close all
clc
clear all
tic;

k0 = linspace(0,2*pi,100);
for kk = 1:100
    k = k0(kk);
    H1 = HH(k);
    [VV,DD] = eig(H1);
    Ds(:,kk) = sort(diag(DD),'ascend'); % sort eigenvalue
end
plot(k0/2/pi,Ds,'k.');
ylim([-1 1])
set(gca,'xtick',[0:0.5:1])
set(gca,'XTickLabel',{'\bf 0','\bf \pi','\bf 2\pi'})
set(gcf,'color','w');
set(gca,'fontsize',16,'LineWidth',1.1);
ylabel('Energy(a.u.)','fontname','Arial');
toc

% define Hamiltonian
function H = HH(k)
N = 10;
M = 0;
t1 = 1;
t2 = 0.03;
phi = pi/2;
h00 = zeros(2 * 4 * N, 2 * 4 * N);
h01 = zeros(2 * 4 * N, 2 * 4 * N);
for spin = 1:2
    for ii = 0:N-1
        % nearest neighbor couplings
        h00(ii * 4 * 2 + 0 * 2 + spin, ii * 4 * 2 + 1 * 2 + spin) = t1;
        h00(ii * 4 * 2 + 1 * 2 + spin, ii * 4 * 2 + 0 * 2 + spin) = t1;
        
        h00(ii * 4 * 2 + 1 * 2 + spin, ii * 4 * 2 + 2 * 2 + spin) = t1;
        h00(ii * 4 * 2 + 2 * 2 + spin, ii * 4 * 2 + 1 * 2 + spin) = t1;
        
        h00(ii * 4 * 2 + 2 * 2 + spin, ii * 4 * 2 + 3 * 2 + spin) = t1;
        h00(ii * 4 * 2 + 3 * 2 + spin, ii * 4 * 2 + 2 * 2 + spin) = t1;
        %next nearest neighbor couplings
        h00(ii * 4 * 2 + 0 * 2 + spin, ii * 4 * 2 + 2 * 2 + spin) = t2 * exp(-1j * phi) * sign_spin(spin);
        h00(ii * 4 * 2 + 2 * 2 + spin, ii * 4 * 2 + 0 * 2 + spin) = conj(h00(...
            ii * 4 * 2 + 0 * 2 + spin, ii * 4 * 2 + 2 * 2 + spin));
        h00(ii * 4 * 2 + 1 * 2 + spin, ii * 4 * 2 + 3 * 2 + spin) = t2 * exp(-1j * phi) * sign_spin(spin);
        h00(ii * 4 * 2 + 3 * 2 + spin, ii * 4 * 2 + 1 * 2 + spin) = conj(h00(...
            ii * 4 * 2 + 1 * 2 + spin, ii * 4 * 2 + 3 * 2 + spin));
        %
    end
    for ii = 0:N-2
        % nearest neighbor couplings
        h00(ii * 4 * 2 + 3 * 2 + spin, (ii + 1) * 4 * 2 + 0 * 2 + spin) = t1;
        h00((ii + 1) * 4 * 2 + 0 * 2 + spin, ii * 4 * 2 + 3 * 2 + spin) = t1;
        
        % next nearest neighbor couplings
        h00(ii * 4 * 2 + 2 * 2 + spin, (ii + 1) * 4 * 2 + 0 * 2 + spin) = t2 *exp(1j * phi) * sign_spin(spin);
        h00((ii + 1) * 4 * 2 + 0 * 2 + spin, ii * 4 * 2 + 2 * 2 + spin) = conj(h00(...
            ii * 4 * 2 + 2 * 2 + spin, (ii + 1) * 4 * 2 + 0 * 2 + spin));
        h00(ii * 4 * 2 + 3 * 2 + spin, (ii + 1) * 4 * 2 + 1 * 2 + spin) = t2 * exp(1j * phi) * sign_spin(spin);
        h00((ii + 1) * 4 * 2 + 1 * 2 + spin, ii * 4 * 2 + 3 * 2 + spin) = conj(h00(...
            ii * 4 * 2 + 3 * 2 + spin, (ii + 1) * 4 * 2 + 1 * 2 + spin) );
    end
    % hopping of intercell h01
    for ii = 0:N-1
        % nearest neighbor couplings
        h01(ii * 4 * 2 + 1 * 2 + spin, ii * 4 * 2 + 0 * 2 + spin) = t1;
        h01(ii * 4 * 2 + 2 * 2 + spin, ii * 4 * 2 + 3 * 2 + spin) = t1;
        
        % next nearest neighbor couplings
        h01(ii * 4 * 2 + 0 * 2 + spin, ii * 4 * 2 + 0 * 2 + spin) = t2 * exp(1j * phi) * sign_spin(spin);
        h01(ii * 4 * 2 + 1 * 2 + spin, ii* 4 * 2 + 1 * 2 + spin) = t2 * exp(-1j * phi) * sign_spin(spin);
        h01(ii * 4 * 2 + 2 * 2 + spin, ii * 4 * 2 + 2 * 2 + spin) = t2 * exp(1j * phi) * sign_spin(spin);
        h01(ii * 4 * 2 + 3 * 2 + spin, ii * 4 * 2 + 3 * 2 + spin) = t2 * exp(-1j * phi) * sign_spin(spin);
        
        h01(ii * 4 * 2 + 1 * 2 + spin, ii * 4 * 2 + 3 * 2 + spin) = t2 * exp(1j * phi) * sign_spin(spin);
        h01(ii * 4 * 2 + 2 * 2 + spin, ii * 4 * 2 + 0 * 2 + spin) = t2 * exp(-1j * phi) * sign_spin(spin);
        if ii ~= 0
            h01(ii * 4 * 2 + 1 * 2 + spin, (ii - 1) * 4 * 2 + 3 * 2 + spin) = t2 * exp(1j * phi) * sign_spin(spin);
        end
    end
   for ii = 0:N-2
    h01(ii * 4 * 2 + 2 * 2 + spin, (ii + 1) * 4 * 2 + 0 * 2 + spin) = t2 *exp(-1j * phi) * sign_spin(spin);
   end
end
H = h00 + h01 * exp(1j * k) + h01' * exp(-1j * k);
end

function sign = sign_spin(spin)
if spin == 1
    sign = 1;
else
    sign = -1;
end
end

运行结果：

8,482 次浏览

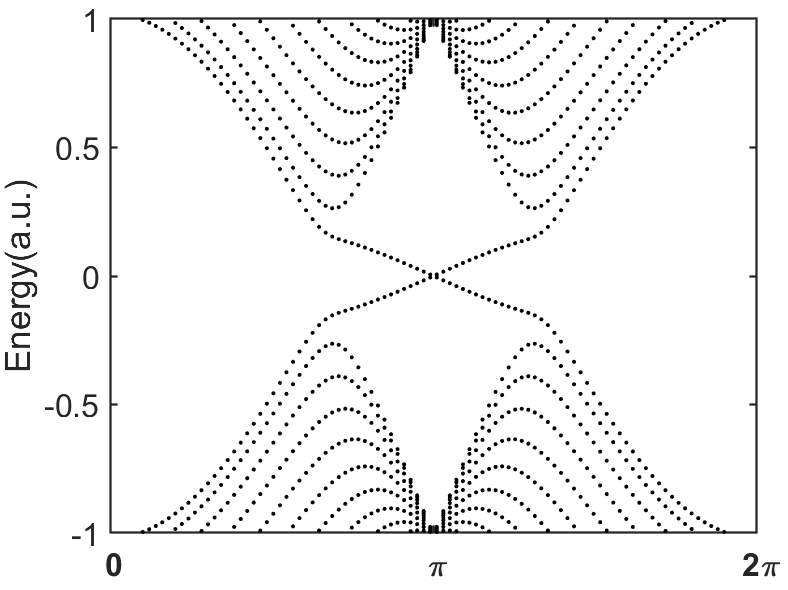
【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】