格林函数中Dyson方程的数值验证（附Python代码）

戴森方程（Dyson equation）为[1]：

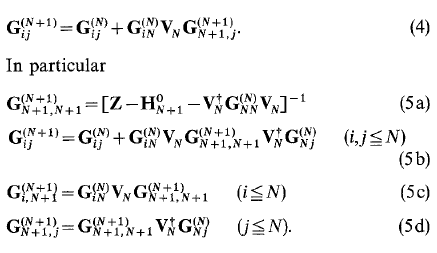
以方格子为例，我们将从数值上验证一下Dyson方程得到的格林函数G_0n和整体格林中对应的分块矩阵是否完全相同。

代码为：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/4396
"""

import numpy as np
import matplotlib.pyplot as plt
import copy
import time


def matrix_00(width):    # 一个切片（slide)内的哈密顿量
    h00 = np.zeros((width, width))
    for width0 in range(width-1):
        h00[width0, width0+1] = 1
        h00[width0+1, width0] = 1
    return h00


def matrix_01(width):    # 切片之间的跃迁项（hopping）
    h01 = np.identity(width)
    return h01


def matrix_whole(width, length):   # 方格子整体的哈密顿量，宽度为width，长度为length
    hamiltonian = np.zeros((width*length, width*length))
    for x in range(length):
        for y in range(width-1):
            hamiltonian[x*width+y, x*width+y+1] = 1
            hamiltonian[x*width+y+1, x*width+y] = 1
    for x in range(length-1):
        for y in range(width):
            hamiltonian[x*width+y, (x+1)*width+y] = 1
            hamiltonian[(x+1)*width+y, x*width+y] = 1
    return hamiltonian


def main():
    width =4   # 方格子的宽度
    length = 200  # 方格子的长度
    h00 = matrix_00(width)  # 一个切片（slide)内的哈密顿量
    h01 = matrix_01(width)   # 切片之间的跃迁项（hopping）
    hamiltonian = matrix_whole(width, length)  # 方格子整体的哈密顿量，宽度为width，长度为length
    fermi_energy = 0.1   # 费米能取为0.1为例。按理来说计算格林函数时，这里需要加上一个无穷小的虚数，但Python中好像不加也不会有什么问题。

    start_1= time.perf_counter()
    green = General_way(fermi_energy, hamiltonian)  # 利用通常直接求逆的方法得到整体的格林函数green
    end_1 = time.perf_counter()
    start_2= time.perf_counter()
    green_0n_n = Dyson_way(fermi_energy, h00, h01, length)  # 利用Dyson方程得到的格林函数green_0n
    end_2 = time.perf_counter()

    # print(green)
    print('\n整体格林函数中的一个分块矩阵green_0n：\n', green[0:width, (length-1)*width+0:(length-1)*width+width])  # a:b代表 a <= x < b，左闭右开
    print('Dyson方程得到的格林函数green_0n：\n', green_0n_n)
    print('观察以上两个矩阵，可以直接看出两个矩阵完全相同。\n')

    print('General_way执行时间=', end_1-start_1) 
    print('Dyson_way执行时间=', end_2-start_2)


def General_way(fermi_energy, hamiltonian):
    dim_hamiltonian = hamiltonian.shape[0]
    green = np.linalg.inv((fermi_energy)*np.eye(dim_hamiltonian)-hamiltonian)
    return green


def Dyson_way(fermi_energy, h00, h01, length):
    dim = h00.shape[0]
    for ix in range(length):
        if ix == 0:
            green_nn_n = np.linalg.inv(fermi_energy*np.identity(dim)-h00)   # 如果有左电极，还需要减去左电极的自能left_self_energy
            green_0n_n = copy.deepcopy(green_nn_n)  # 如果直接用等于，两个变量会指向相同的id，改变一个值，另外一个值可能会发生改变，容易出错，所以要用上这个COPY
        elif ix != length-1:
            green_nn_n = np.linalg.inv(fermi_energy*np.identity(dim)-h00-np.dot(np.dot(h01.transpose().conj(), green_nn_n), h01))
            green_0n_n = np.dot(np.dot(green_0n_n, h01), green_nn_n)
        else:  # 这里和（elif ix != length-1）中的内容完全一样，但如果有右电极，这里是还需要减去右电极的自能right_self_energy
            green_nn_n = np.linalg.inv(fermi_energy*np.identity(dim)-h00-np.dot(np.dot(h01.transpose().conj(), green_nn_n), h01))  
            green_0n_n = np.dot(np.dot(green_0n_n, h01), green_nn_n)
    return green_0n_n


if __name__ == '__main__':
    main()

计算结果为：

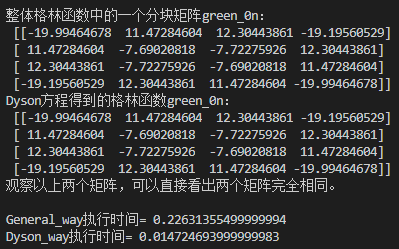
结论：

Dyson方程得到的格林函数green_0n和体系的整体格林函数green中的一个对应分块矩阵green_0n完全对应。

同时可以发现，用Dyson方程的计算方法比通常方法时间用更少，这是因为整体格林函数包含了所有的信息，而利用Dyson方程，我们只需要计算需要的那个分块矩阵即可。数值上的理解是，Dyson方程只需要对width维的矩阵求逆，而通常的方法是需要对width*length维的矩阵求逆，耗的时间更多【矩阵求逆的时间复杂度为O(n^3)】。尤其是当length足够长时，这个计算时间的差别会更加明显。

参考资料：

[1] The calculation of transport properties and density of states of disordered solids

[2] F. J. Dyson, The S Matrix in Quantum Electrodynamics, Phys. Rev. 75: 1736.

2,955 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】