这是之前的一篇:用于概率事件中决策的凯利公式。
本篇给出凯利公式的 Python 数值验证代码,并对做决策的次数进行讨论。
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/43508
"""
import numpy as np
import matplotlib.pyplot as plt
investment_ratio_array = np.arange(0.1, 1.1, 0.1)
investment_times = 1000
test_times = 100
# 几个例子:https://www.guanjihuan.com/archives/43412
# 例子(2)的参数
p = 0.6 # 胜率
b = 1 # 收益
a = 1 # 损失
# # 例子(3)的参数
# p = 0.5
# b = 1
# a = 0.5
win_array = [] # 胜出的仓位
for i0 in range(test_times):
# print(i0)
capital_array = []
for f in investment_ratio_array:
capital = 1
for _ in range(investment_times):
investment = capital*f
if investment>0:
random_value = np.random.uniform(0, 1)
if random_value<p:
capital = capital+investment*b
else:
capital = capital-investment*a
capital_array.append(capital)
max_capital_index = capital_array.index(max(capital_array))
win_array.append(investment_ratio_array[max_capital_index])
def kelly_formula(p, b, a):
f=(p/a)-((1-p)/b)
return f
print(kelly_formula(p=p, b=b, a=a))
plt.hist(win_array, bins=100, color='skyblue')
plt.show()以下是运行结果。可以看出,只有当独立做决策的次数的成百上千时,凯利公式才会发挥作用。有时 100 次的决策还不一定稳定,可能需要到 1000 次。
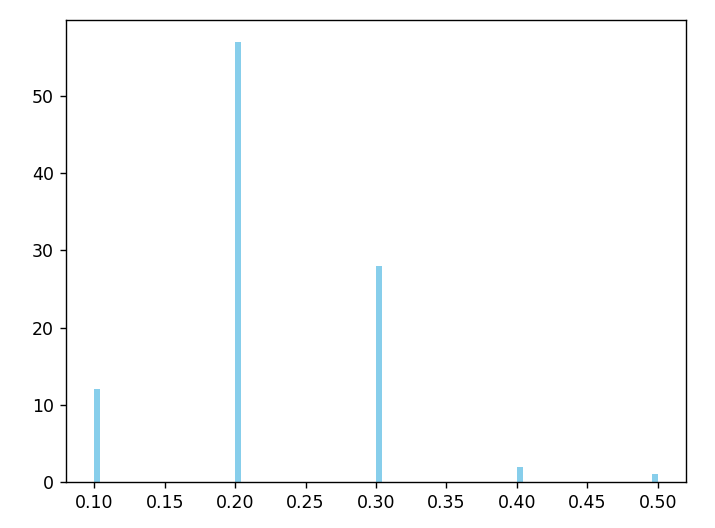
一、
investment_times = 1000
# 例子(2)的参数
p = 0.6 # 胜率
b = 1 # 收益
a = 1 # 损失对应的结果为:
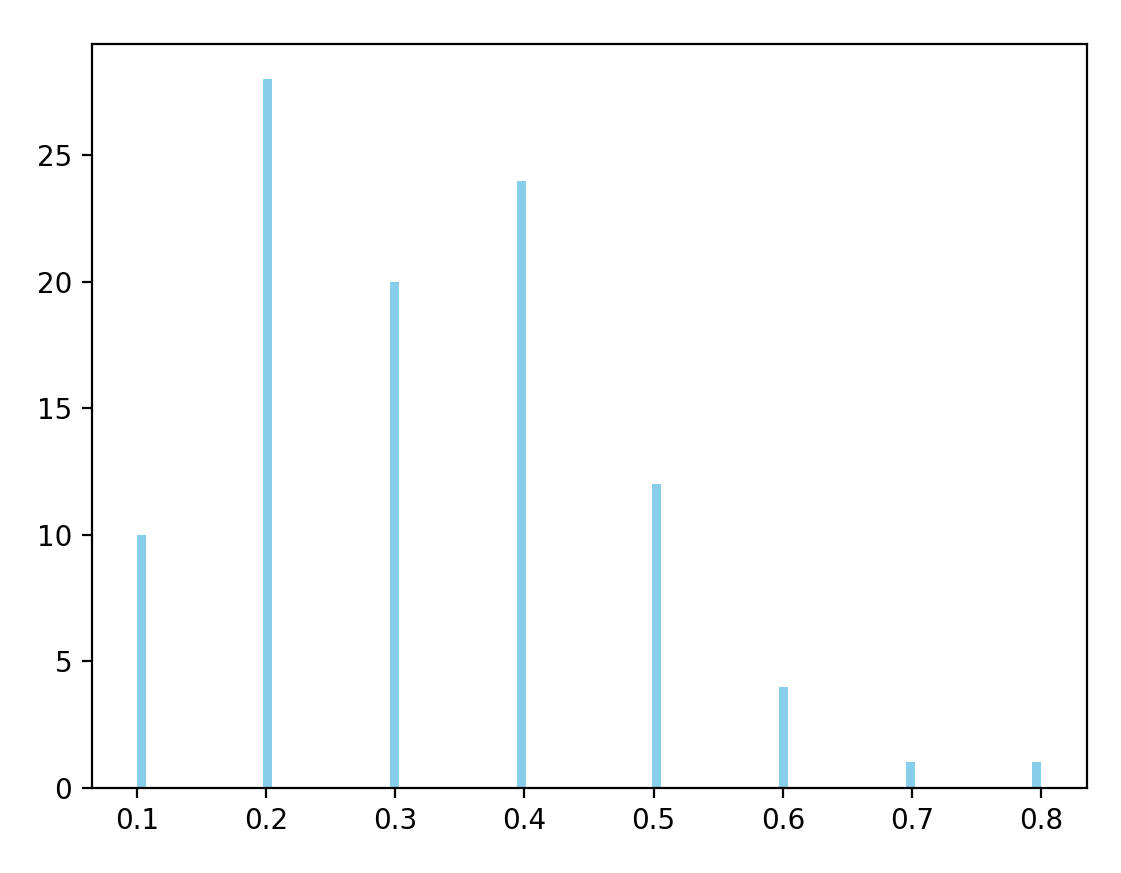
二、
investment_times = 100
# 例子(2)的参数
p = 0.6 # 胜率
b = 1 # 收益
a = 1 # 损失对应的结果是:
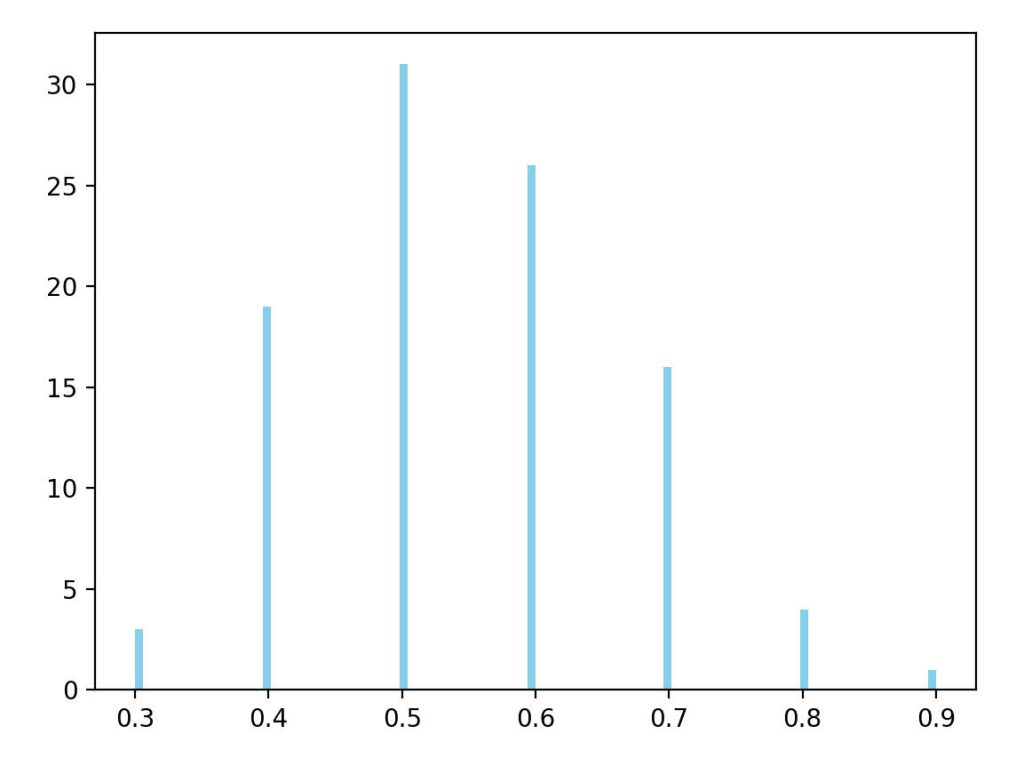
三、
investment_times = 1000
# 例子(3)的参数
p = 0.5
b = 1
a = 0.5对应的结果是:
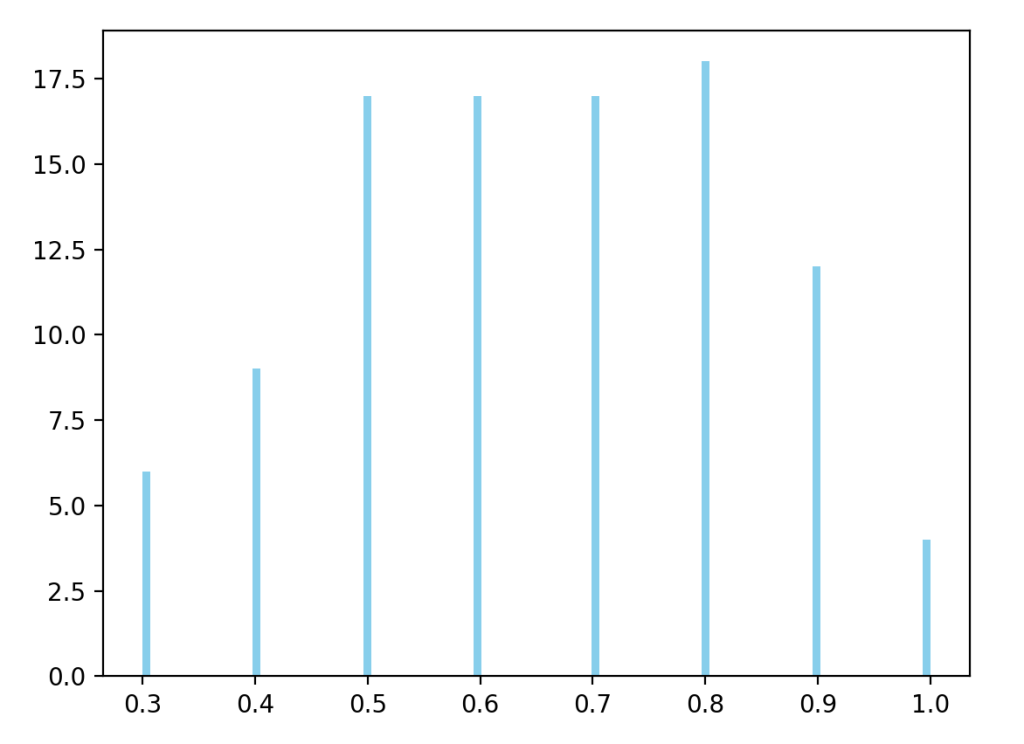
四、
investment_times = 100
# 例子(3)的参数
p = 0.5
b = 1
a = 0.5对应的结果是:
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】