双层石墨烯哈密顿量与能带图（附Python代码）

双层石墨烯哈密顿量主要参考这篇文献：Localized States at Zigzag Edges of Bilayer Graphene。

在实空间中，双层石墨烯哈密顿量写为

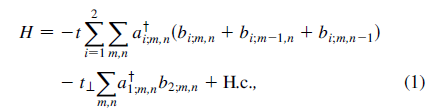
当y方向受限，宽度为N，x方向傅里叶变换后，得到（文献中给出的表达式）：

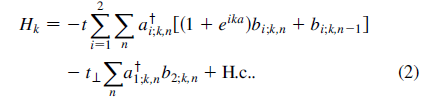
可以改写为矩阵形式（略去矩阵前后的基矢），这里是以N=3为例：

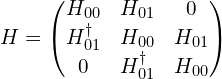
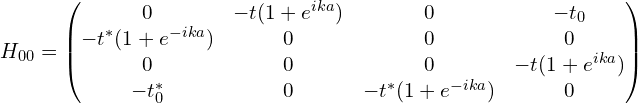
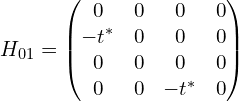
手稿为（这里也略去矩阵前后的基矢，但标出了对应的基矢的位置）：

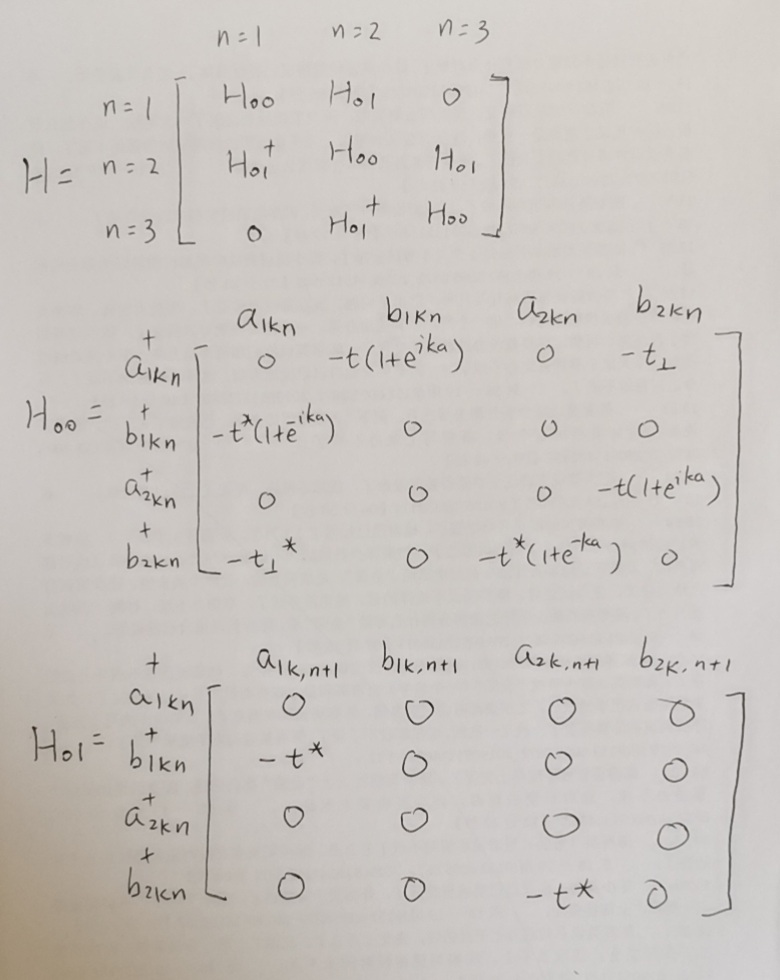
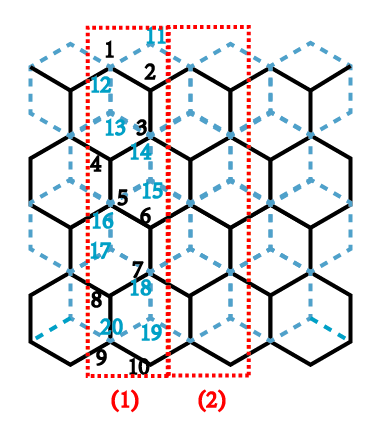
以上这种形式，对应的编号如下图所示（这里是以N=5为例 ）。

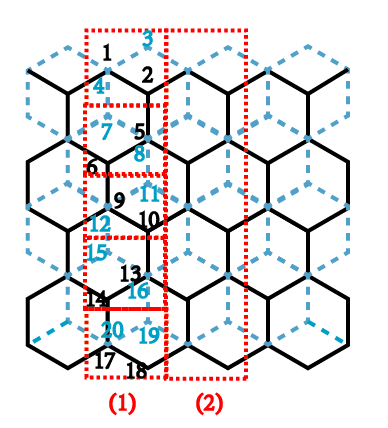
代码为：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/4322
"""

import numpy as np
import matplotlib.pyplot as plt
from math import * 
import cmath 
import functools


def hamiltonian(k, N):  
    # 初始化为零矩阵
    h = np.zeros((4*N, 4*N), dtype=complex)

    t=1
    a=1
    t0=0.2   # 层间跃迁
    V=0.2    # 层间的势能差为2V

    for i in range(N):
        h[i*4+0, i*4+0] = V
        h[i*4+1, i*4+1] = V
        h[i*4+2, i*4+2] = -V
        h[i*4+3, i*4+3] = -V

        h[i*4+0, i*4+1] = -t*(1+cmath.exp(1j*k*a))
        h[i*4+1, i*4+0] = -t*(1+cmath.exp(-1j*k*a))
        h[i*4+2, i*4+3] = -t*(1+cmath.exp(1j*k*a))
        h[i*4+3, i*4+2] = -t*(1+cmath.exp(-1j*k*a))

        h[i*4+0, i*4+3] = -t0
        h[i*4+3, i*4+0] = -t0

    for i in range(N-1):
        # 最近邻
        h[i*4+1, (i+1)*4+0] = -t
        h[(i+1)*4+0, i*4+1] = -t

        h[i*4+3, (i+1)*4+2] = -t
        h[(i+1)*4+2, i*4+3] = -t
    return h


def main():
    hamiltonian0 = functools.partial(hamiltonian, N=100)
    k = np.linspace(-pi, pi, 400)
    plot_bands_one_dimension(k, hamiltonian0)


def plot_bands_one_dimension(k, hamiltonian):
    dim = hamiltonian(0).shape[0]
    dim_k = k.shape[0]
    eigenvalue_k = np.zeros((dim_k, dim))
    i0 = 0
    for k0 in k:
        matrix0 = hamiltonian(k0)
        eigenvalue, eigenvector = np.linalg.eig(matrix0)
        eigenvalue_k[i0, :] = np.sort(np.real(eigenvalue[:]))
        i0 += 1
        print(k0)
    for dim0 in range(dim):
        plt.plot(k, eigenvalue_k[:, dim0], '-k')
    plt.show()


if __name__ == '__main__':
    main()

计算结果为：

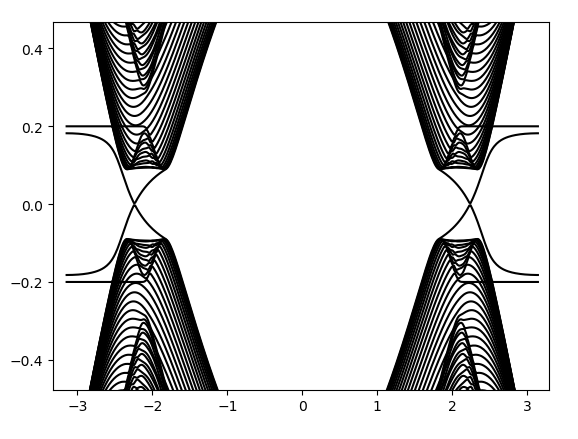
此外，也可以按照层的顺序依次编号，如下图所示（编号顺序不影响计算的结果）：

这时的代码写为：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/4322
"""

import numpy as np
import matplotlib.pyplot as plt
from math import * 
import cmath 
import functools 


def hamiltonian(k, N):  
    # 初始化为零矩阵
    h = np.zeros((4*N, 4*N), dtype=complex)
    h11 = np.zeros((4*N, 4*N), dtype=complex)  # 元胞内
    h12 = np.zeros((4*N, 4*N), dtype=complex)  # 元胞间

    t=1
    a=1
    t0=0.2   # 层间跃迁
    V=0.2    # 层间的势能差为2V

    for i in range(N):
        h11[i*2+0, i*2+0] = V
        h11[i*2+1, i*2+1] = V


        h11[N*2+i*2+0, N*2+i*2+0] = -V
        h11[N*2+i*2+1, N*2+i*2+1] = -V


        h11[i*2+0, i*2+1] = -t 
        h11[i*2+1, i*2+0] = -t


        h11[N*2+i*2+0, N*2+i*2+1] = -t
        h11[N*2+i*2+1, N*2+i*2+0] = -t

        h11[i*2+0, N*2+i*2+1] = -t0
        h11[N*2+i*2+1, i*2+0] = -t0


    for i in range(N-1):
        h11[i*2+1, (i+1)*2+0] = -t 
        h11[(i+1)*2+0, i*2+1] = -t

        h11[N*2+i*2+1, N*2+(i+1)*2+0] = -t
        h11[N*2+(i+1)*2+0, N*2+i*2+1] = -t


    for i in range(N):
        h12[i*2+0, i*2+1] = -t
        h12[N*2+i*2+0, N*2+i*2+1] = -t

    h= h11 + h12*cmath.exp(-1j*k*a) + h12.transpose().conj()*cmath.exp(1j*k*a)    
    return h


def main():
    hamiltonian0 = functools.partial(hamiltonian, N=100) 
    k = np.linspace(-pi, pi, 400)
    plot_bands_one_dimension(k, hamiltonian0)


def plot_bands_one_dimension(k, hamiltonian):
    dim = hamiltonian(0).shape[0]
    dim_k = k.shape[0]
    eigenvalue_k = np.zeros((dim_k, dim))
    i0 = 0
    for k0 in k:
        matrix0 = hamiltonian(k0)
        eigenvalue, eigenvector = np.linalg.eig(matrix0)
        eigenvalue_k[i0, :] = np.sort(np.real(eigenvalue[:]))
        i0 += 1
        print(k0)
    for dim0 in range(dim):
        plt.plot(k, eigenvalue_k[:, dim0], '-k') 
    plt.show()


if __name__ == '__main__':
    main()

计算得到的能带和之前编号的结果的相同。

关于单层石墨烯，可阅读这篇：石墨烯哈密顿量与能带图（附Python代码）

8,569 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】