高陈数的蜂窝双层系统中的拓扑隐藏相变 Topological hidden phase transition in honeycomb bilayers with a high Chern number

原文

Ji-Huan Guan, Wen-Kai Lou*, and Kai Chang*, Topological hidden phase transition in honeycomb bilayers with a high Chern number, Phys. Rev. B 110, 165303 (2024). [Editors' Suggestion]

评价：一般来说，价带内部的拓扑不变量的变化很难体现在量子输运的测量中，但通过研究发现，在这个复合蜂窝双层结构中，半反手性边缘态 (half-antichiral edge states) 2e²/h 的电导平台的出现可以作为拓扑隐藏相变 (Topological hidden phase transition) 的一个重要指标或测量方法。

摘要

根据体边对应关系，在量子反常霍尔系统中一维条带通常在两条边上表现出两个无能隙的边缘态，可以由陈数来描述。这里我们引入了一个模型，该模型展示了一种被称为“半反手性”边缘模式的现象。该模型为霍尔丹模型层和修改后的霍尔丹模型层组成的复合双层系统。“半反手性”边缘态在同一边缘上沿相同方向传播，并且通过体内的反向传播模式得到补偿。在强层间耦合的情况下，借助霍尔丹模型层中的手性边缘态，“半反手性”边缘态在整个系统中在无序下表现出比较强的稳定性，从而形成双电导平台。有趣的是，在这一过程中，我们观察到一种拓扑隐藏相变，其中，价带由陈数 C=±(1+1) 演变成一个具有高陈数 C=±2 的价带和一个陈数为 C=0 的平凡价带，这和双电导平台密切相关。这些研究发现为发展层辅助的拓扑态以及在具有高陈数的系统中研究新的拓扑相变提供了更多的可能性。

目录隐藏

原文

摘要

4. 鲁棒的半反手性边缘态和拓扑隐藏相变的关系

5. 更多内容

6. 总结

7. 代码开源

代码一

代码二

1. 主要研究背景

Question & Motivation 1：

根据体边对应关系，拓扑手性边缘态的稳定性由价带的总陈数来决定。而价带内部的陈数变化，即拓扑隐藏相变 (topological hidden phase transition)，是否也可以反应在量子输运中？

Question & Motivation 2：

由于反手性边缘态 (antichiral edge states) 由手征对称性 (chiral symmetry) 保护，其抗无序的能力会比手性边缘态弱很多。那么，是否有办法提高反手性边缘态的量子输运性质？

手性边缘态和反手性边缘态的示意图：

手性边缘态和反手性边缘态的量子输运性质对比：

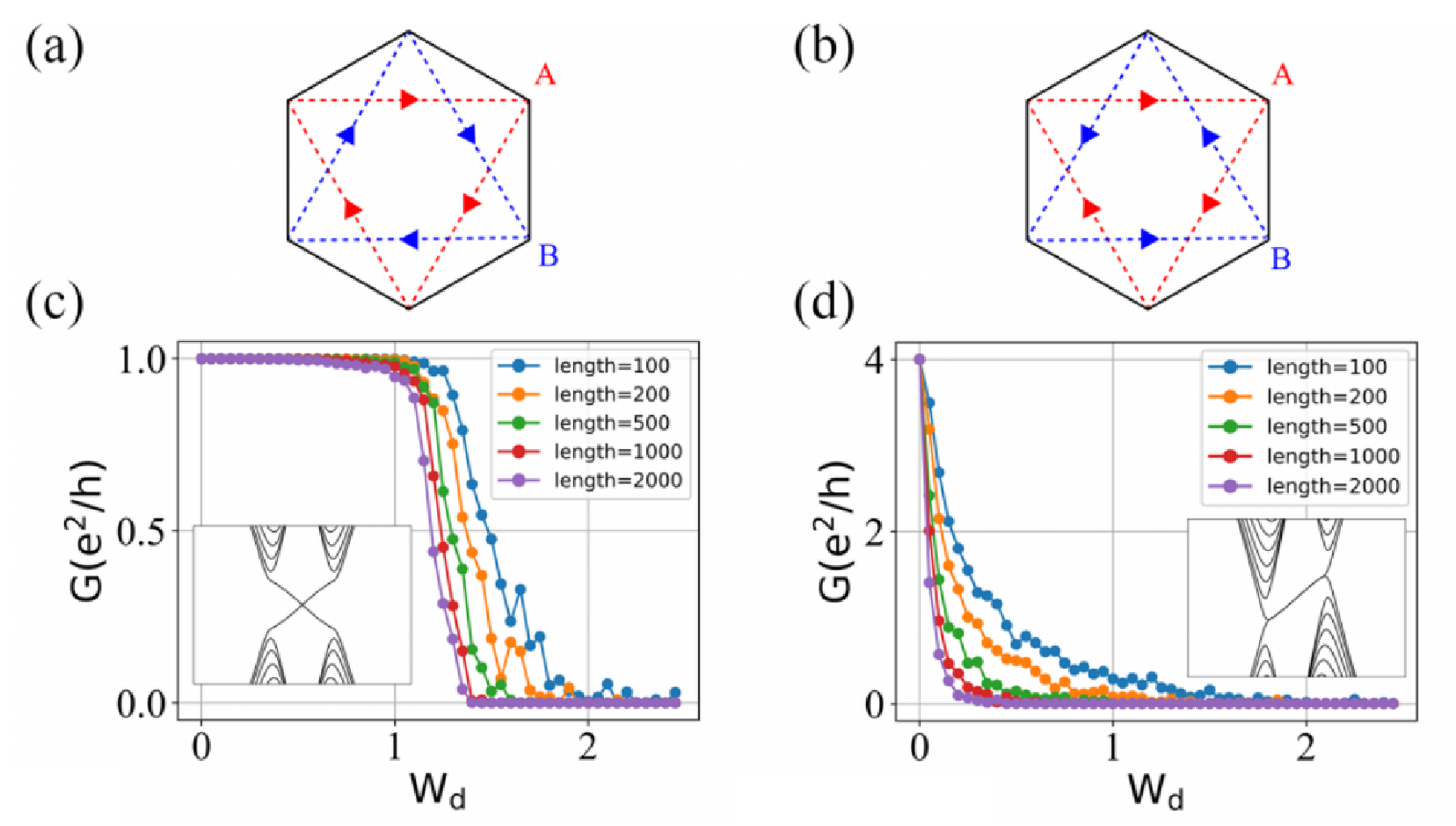
结论：虽然反手性边缘态已经在光学晶体、声子晶格、电路等系统中得到了观测，也具有一定的鲁棒性，但和手性边缘态对比来说，其抗无序的能力会弱很多。

2. 蜂窝双层系统中的半反手性边缘态

2.1 哈密顿量

蜂窝双层系统示意图：

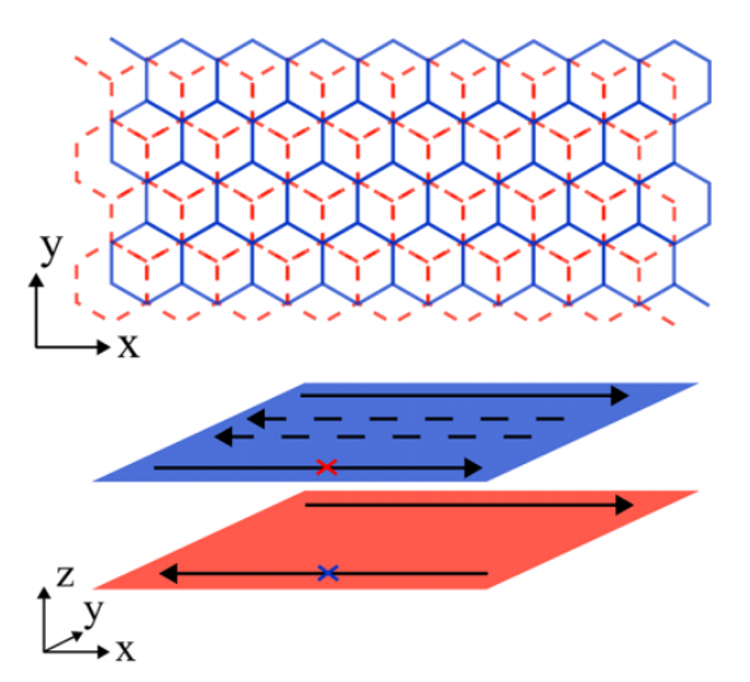
实空间哈密顿量：

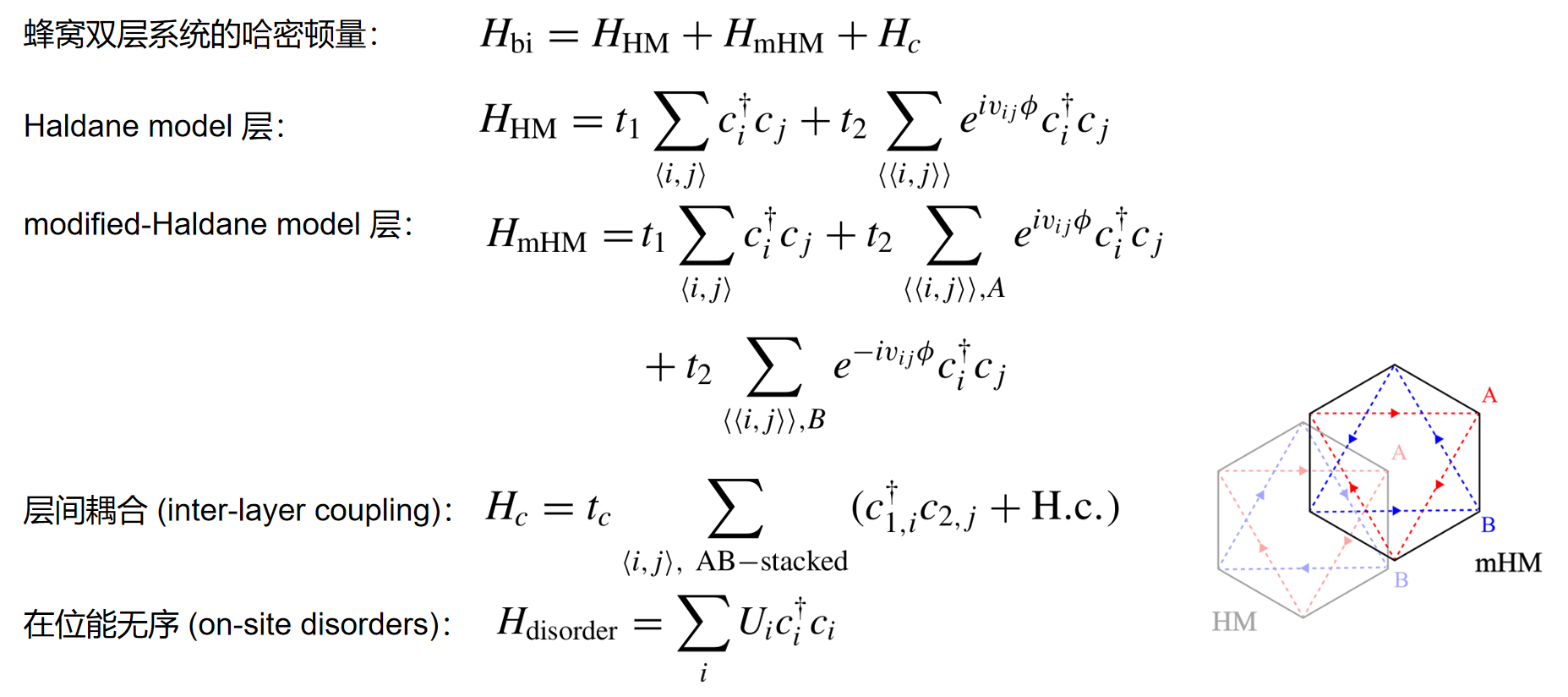
2.2 能带结构

Haldane model (HM) ribbon 的能带结构（可以看到手性边缘态）：

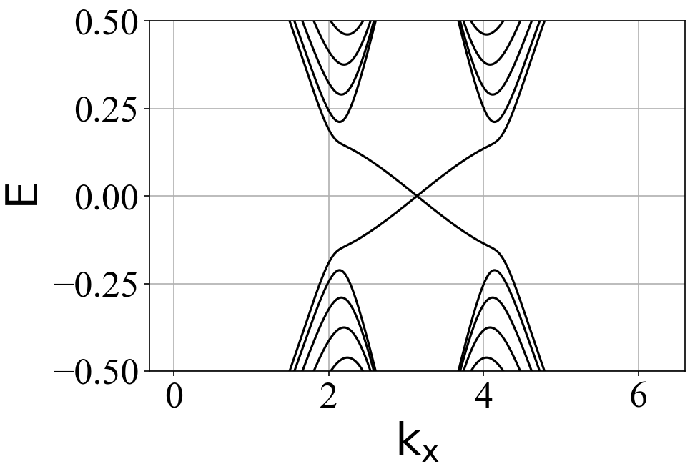
modified-Haldane model (mHM) ribbon 的能带结构（可以看到反手性边缘态）：

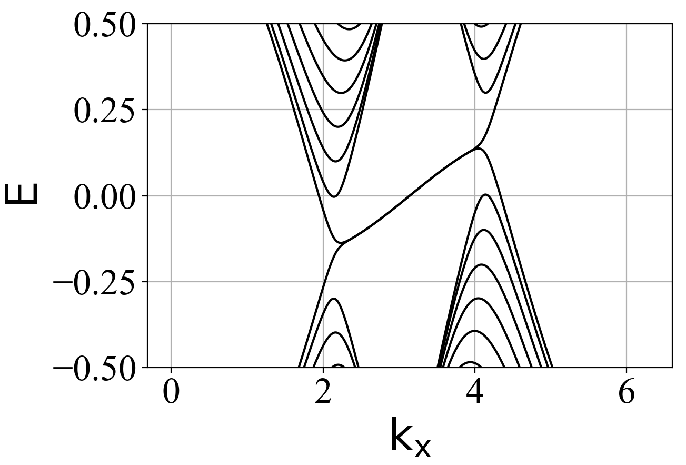
蜂窝双层系统的能带结构（在不同层间耦合强度 t_c 下）：

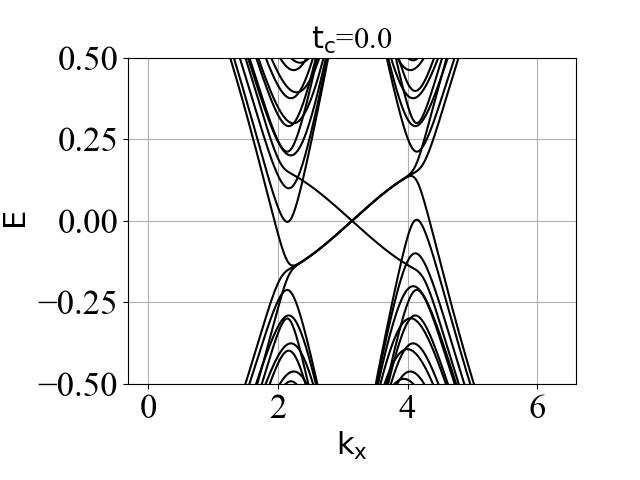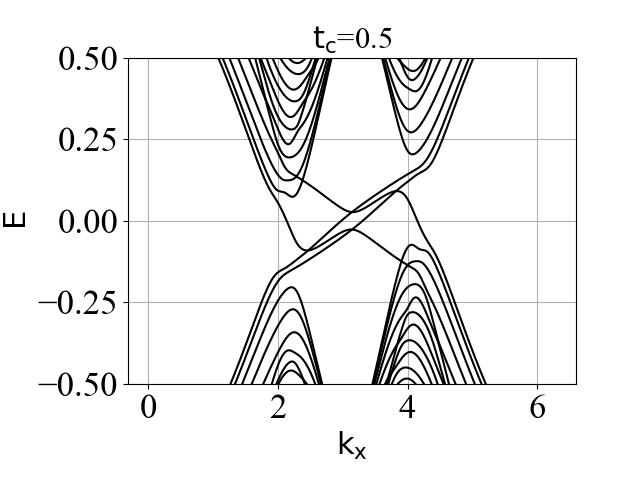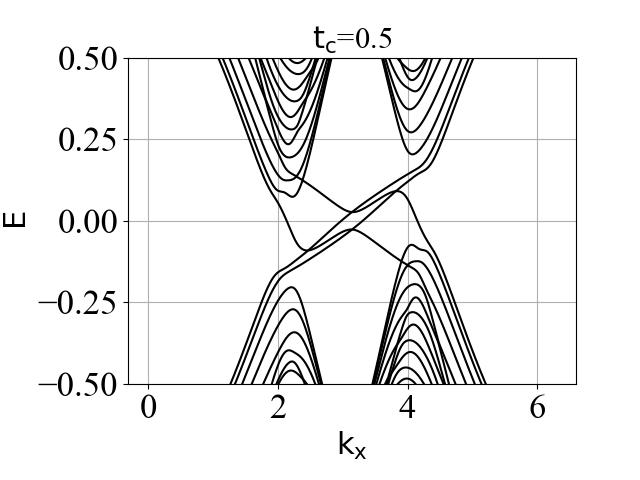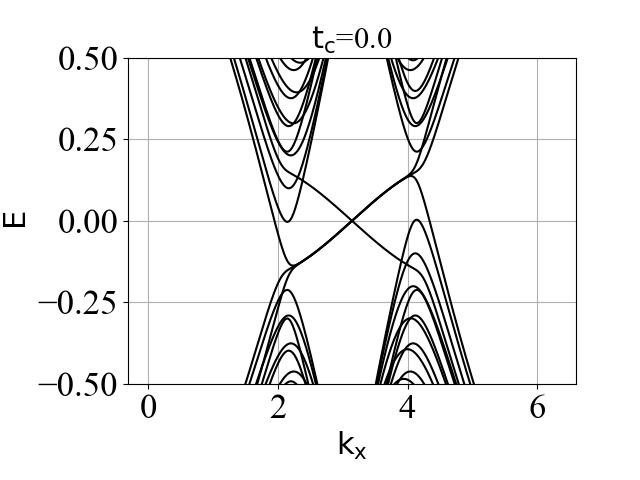
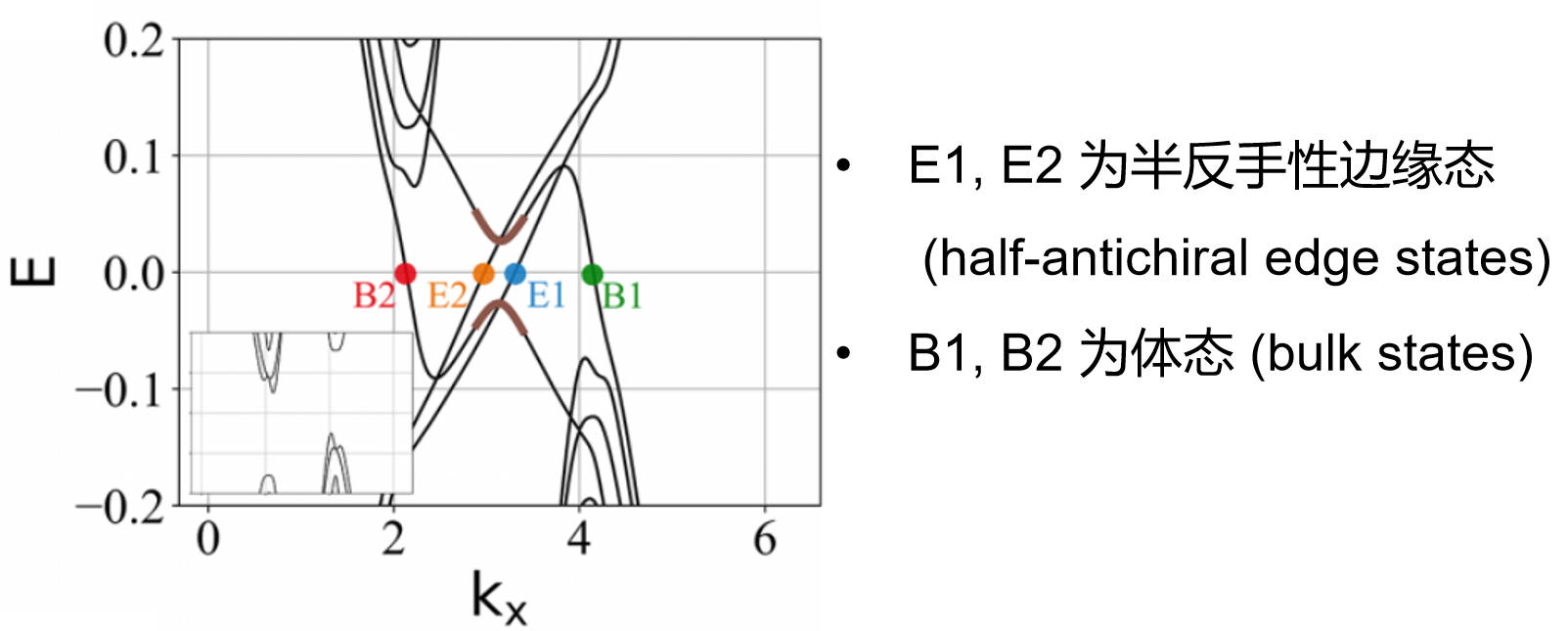
2.3 波函数分布

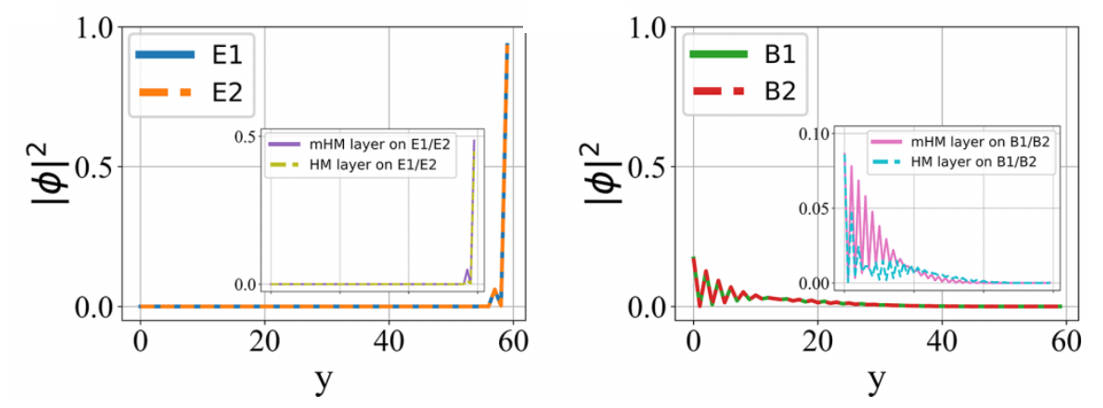
可以看出：

E1, E2 的波函数分布只在条带的一个边缘上，且均匀分布在 HM, mHM 层上。
B1, B2 的波函数分布在条带的内部，但偏向条带的另一个边缘，它主要分布在 mHM 层上。

2.4 量子输运性质

无层间耦合（左图）和强层间耦合（右图）下的量子输运性质：

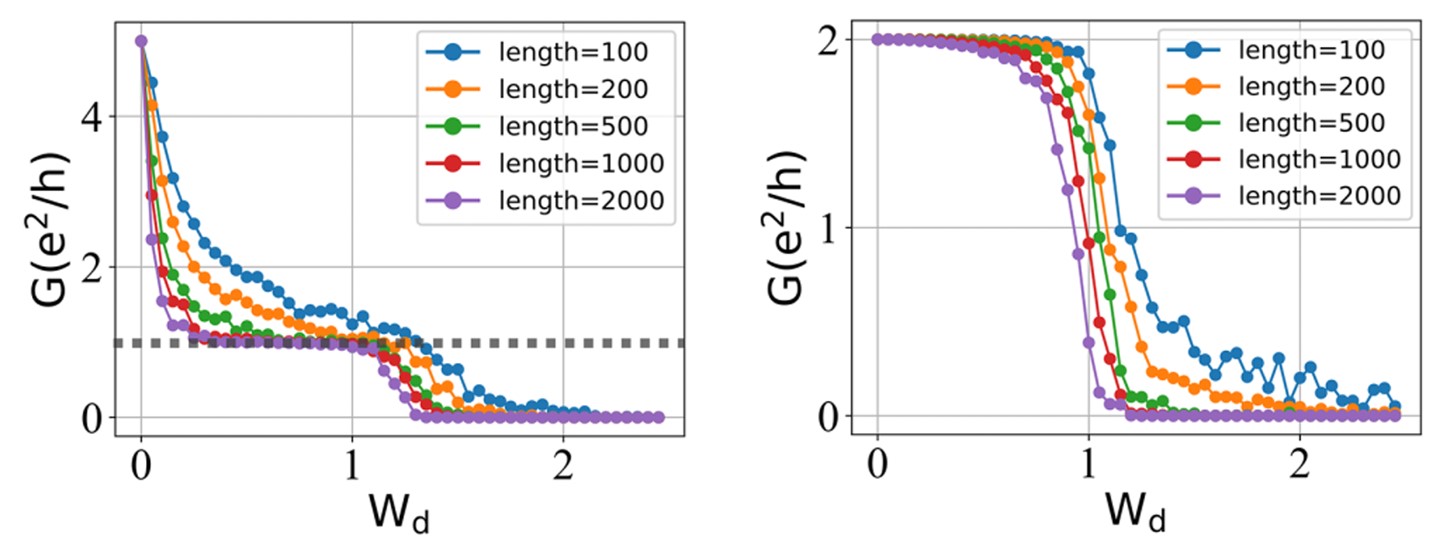
可以看出：

在无层间耦合下，电导随无序的变化情况为两个单层的电导图的叠加，有一个 e²/h 的电导平台。
有意思的是：在强层间耦合下，电导可以稳定到 2e²/h 的平台上。

不同层间耦合强度 t_c 下的量子输运性质：

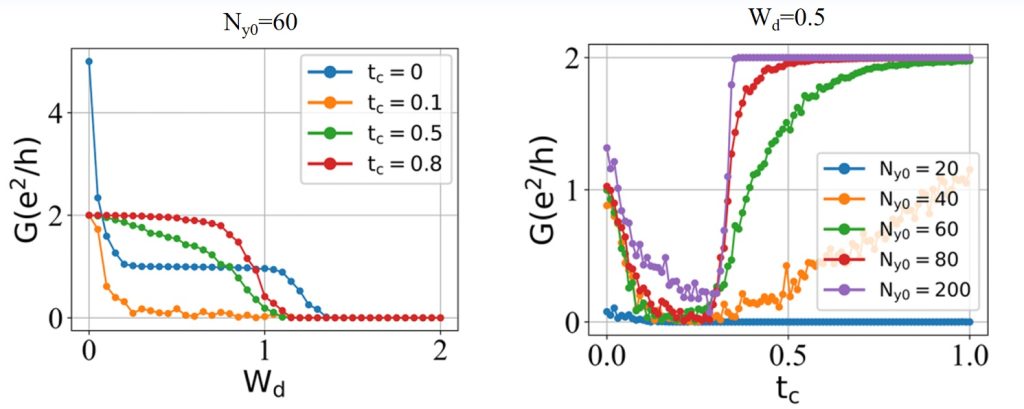
主要结论：随着层间耦合强度 t_c 的增加，电导 G 先减小后增加，会从 e²/h 的平台（左图蓝线）到 2e²/h 的平台（左图红线）。这从右图中也能看出来。

这说明了存在两个散射过程的竞争：（1）HM 层的手性边缘态被体态散射后减弱量子输运；（2）mHM 层的反手性边缘态和 HM 层的手性边缘态互相散射增强输运。

不同条带宽度下的量子输运性质：

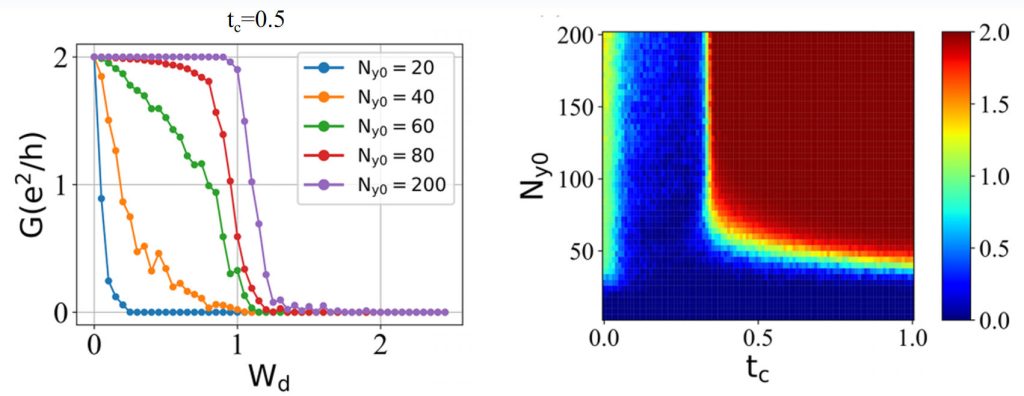
主要现象：

现象1（左图）：随着条带宽度的增加，电导维持在 2e²/h 的平台能力越强。这说明了量子输运过程中受到体态散射的影响。
现象2（右图）：可以看到当条带宽度 N_y0 足够大时，有一个临界值 t_c，这个突变现象无法简单从散射过程的角度来解释。

3. 蜂窝双层系统中的拓扑隐藏相变

Haldane model 二维系统的能带结构（k_y=0）：

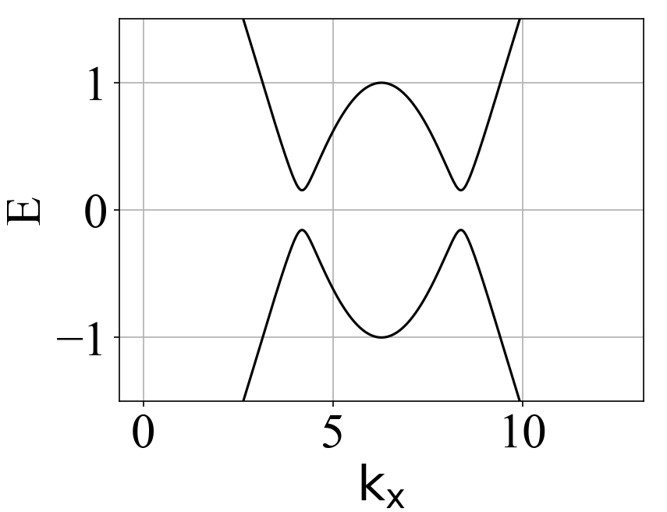
modified-Haldane model 二维系统的能带结构（k_y=0）：

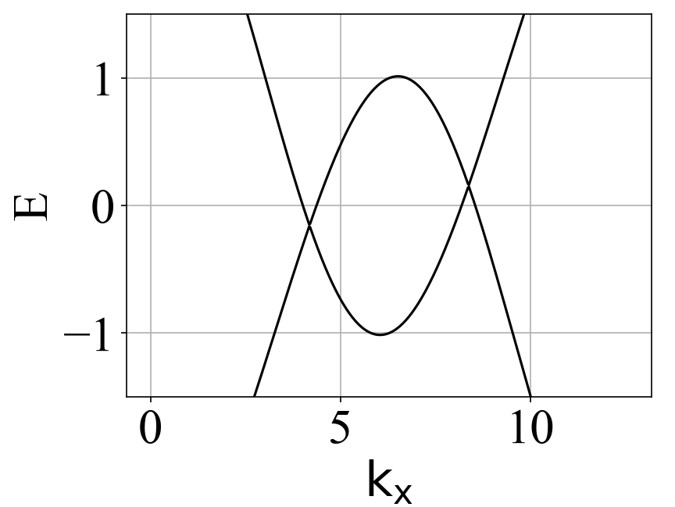
二维蜂窝双层系统的能带结构（k_y=0，在不同层间耦合强度 t_c 下）：

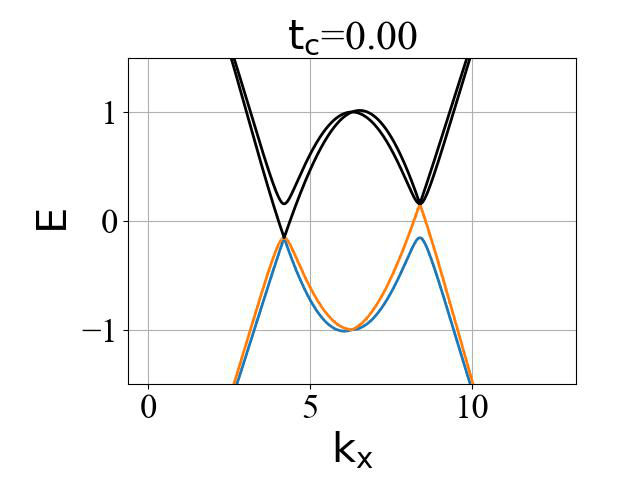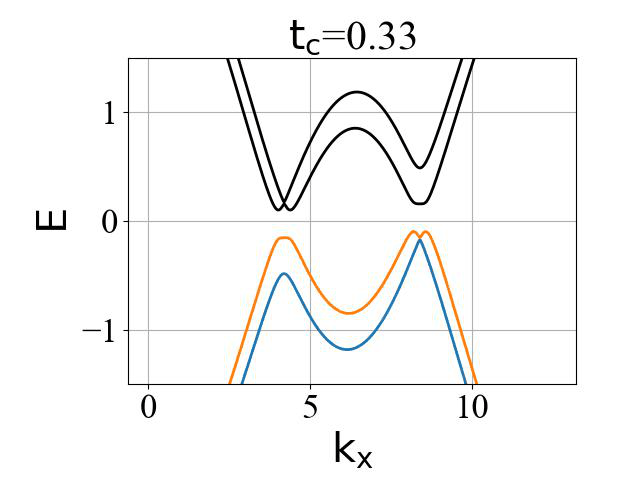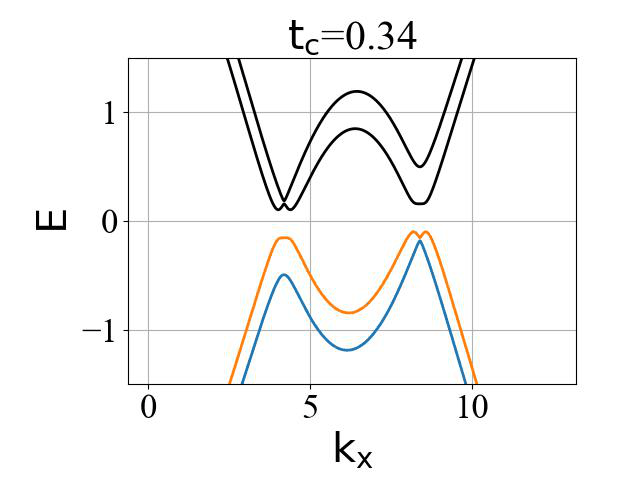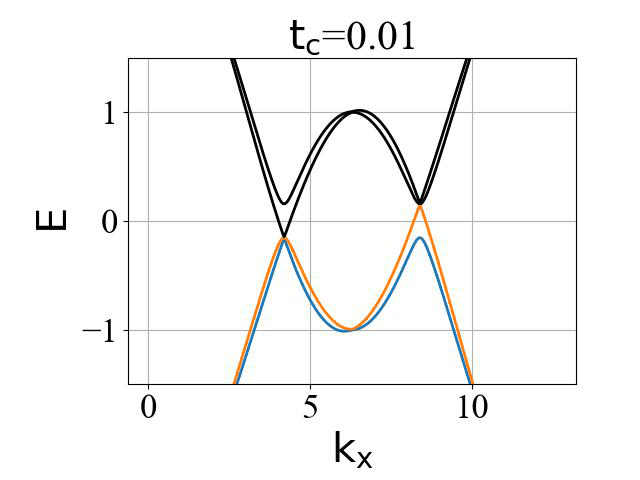
对应的准一维条带系统的能带结构（条带宽度 N_y0 需要选取得足够大，这里选为 200）：

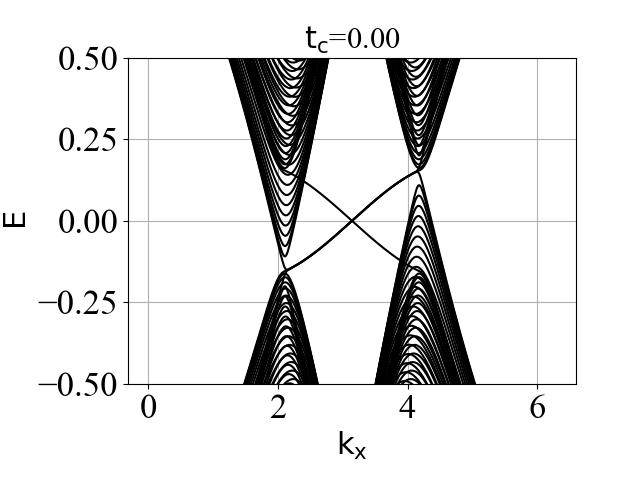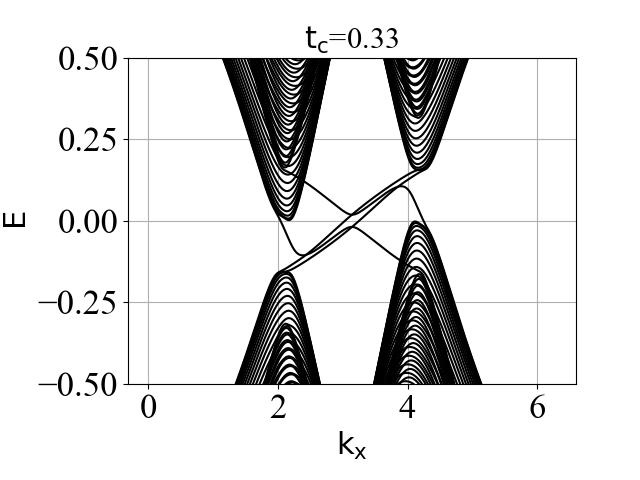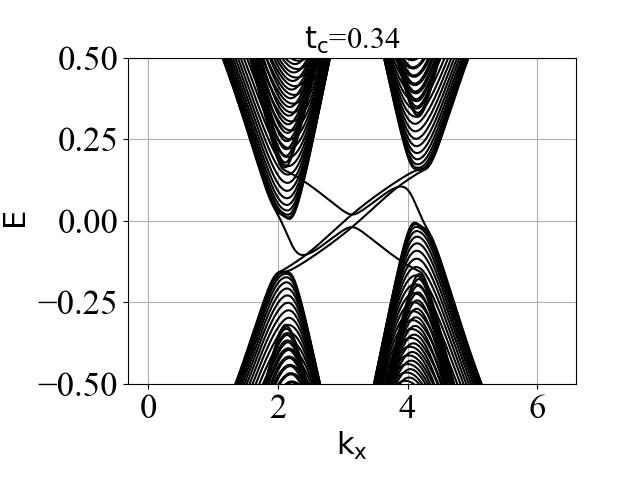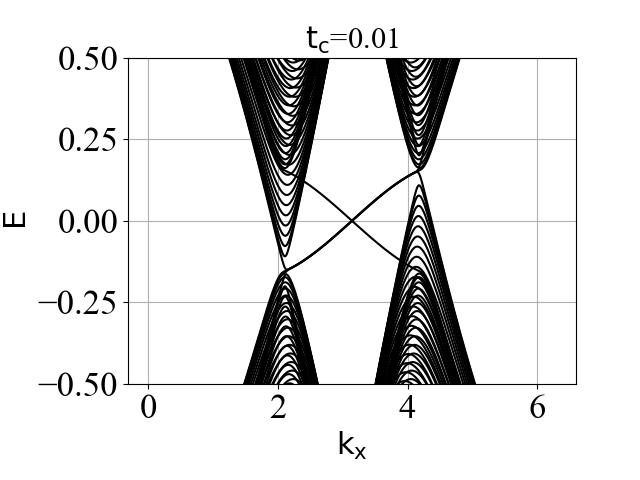
二维系统和准一维条带系统的能带结构对比：

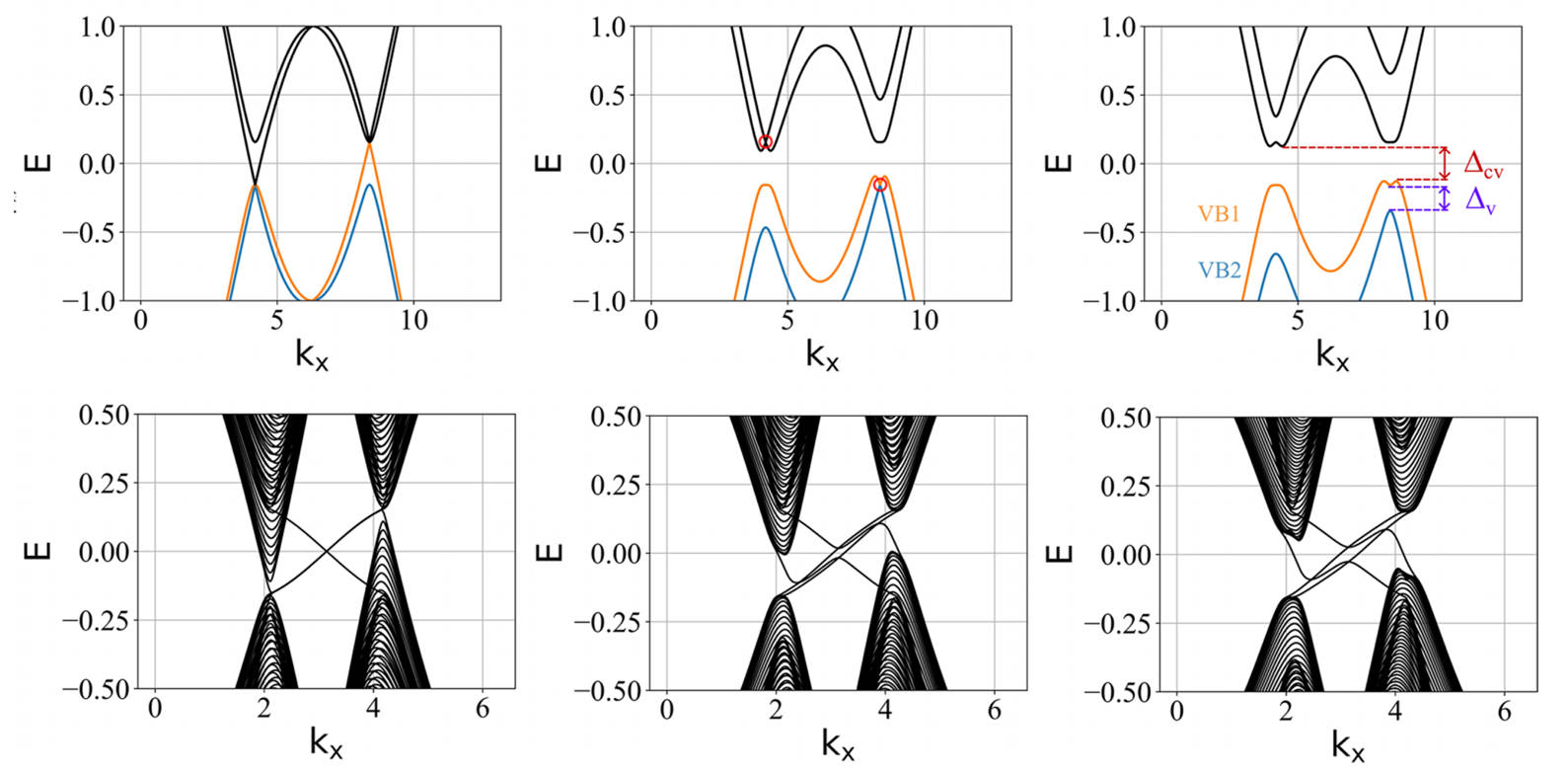
可以看出：发生拓扑隐藏相变时，对应的条带能带的主要体带隙刚好为打开状态。这是因为在比较强的层间耦合下，如果要发生拓扑隐藏相变，那么原先的 mHM 半金属的能带结构（狄拉克锥）需要往导带或价带内部收，从而形成这个条带的间接带隙。

陈数 C、电导 G、带隙 ∆ 随层间耦合强度的变化情况：

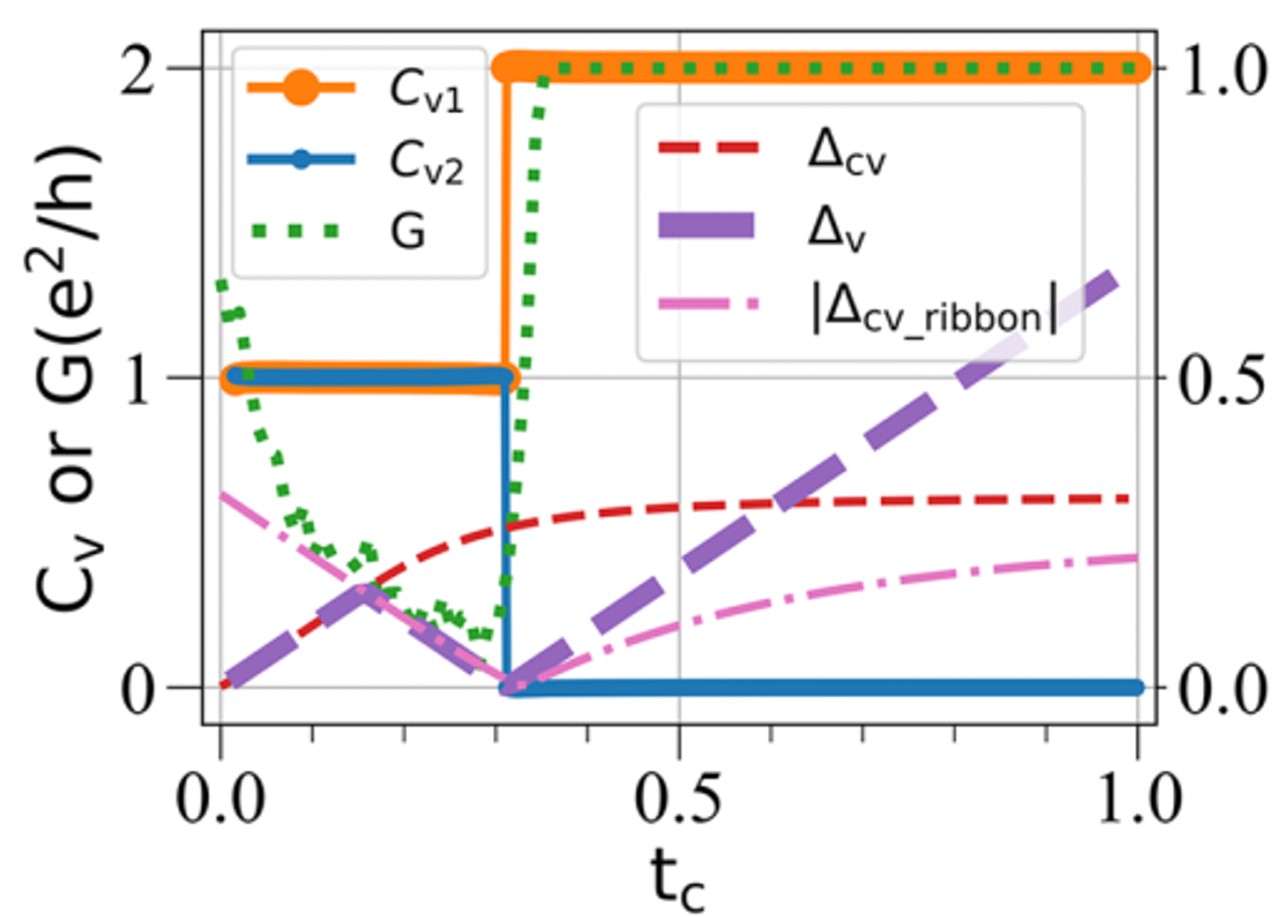
结论：

价带内部陈数（C_v1和C_v2）变化的 t_c 临界值和价带内部的带隙 ∆_v 变化的 t_c 临界值是一致的，在 0.31 附近。
电导 G 变化的 t_c 临界值和条带系统能带结构的带隙 ∆_{cv_ribbon} 变化的 t_c 临界值是一致的，也在 0.31 附近。这个数值是偶然的吗？下面给出了具体的分析。

4. 鲁棒的半反手性边缘态和拓扑隐藏相变的关系

陈数 C、电导 G、带隙 ∆ 在不同次近邻跃迁强度 t₂ 下随层间耦合 tc 的变化情况：

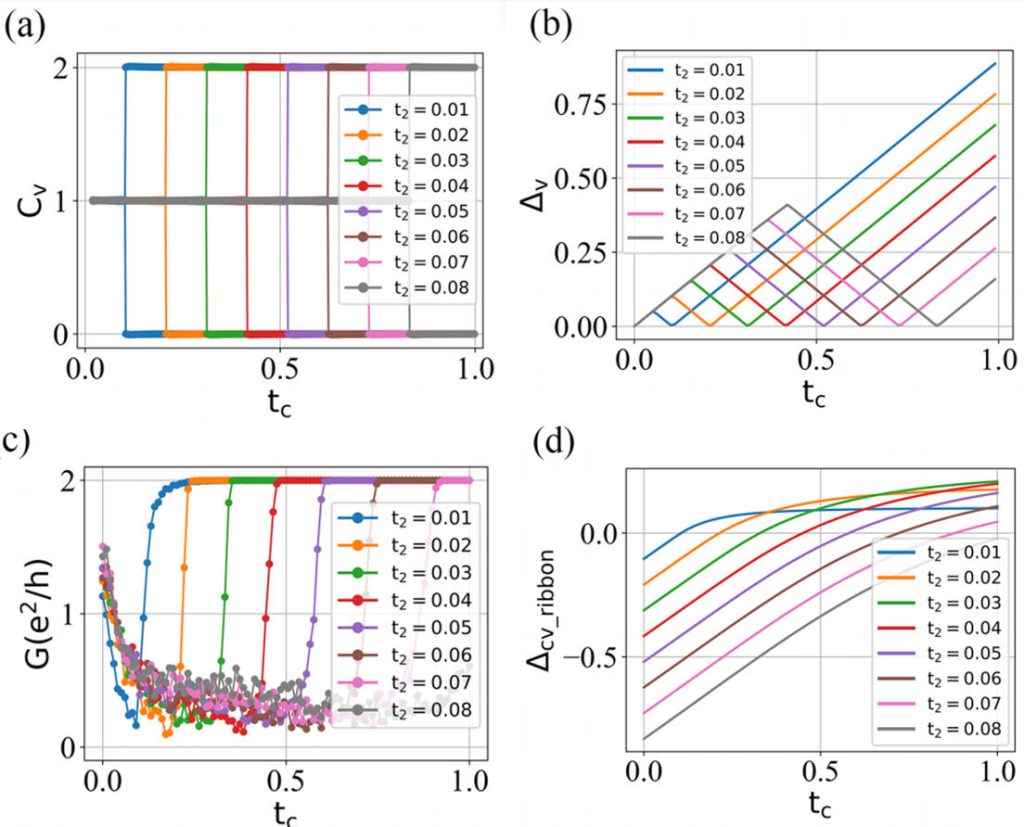
可以发现，当次近邻跃迁强度 t₂ 越大，所需要的临界层间耦合强度 t_c 也越大。

t_c 临界值的总结：

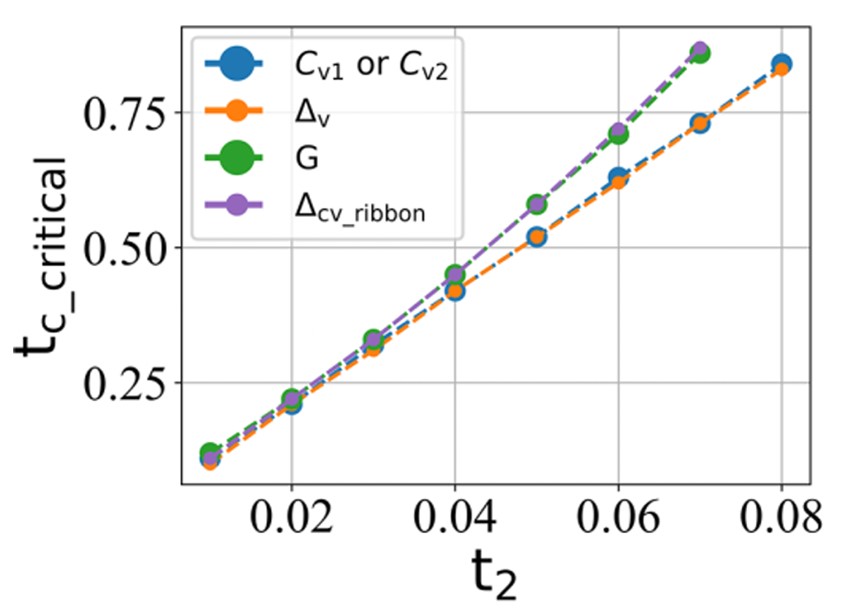
结论：

价带内部陈数（C_v1和C_v2）变化的 t_c 临界值和价带内部的带隙 ∆_v 变化的 t_c 临界值是一致的。
电导 G 变化的 t_c 临界值和条带系统能带结构的带隙 ∆_{cv_ribbon} 变化的 t_c 临界值是一致的。
随着 t₂ 的增加，电导达到 2e²/h 的平台所需要的 t_c 值会略大于发生拓扑隐藏相变所需要的 t_c 值。
然而对于实际体系，次近邻跃迁强度 t₂ 通常是比较小的，因此它们保持了一致性。电导为 2e²/h 的平台可以作为拓扑隐藏相变的一个重要的判断指标。

一个较大的次近邻跃迁强度 t₂ 的例子（层间耦合强度 t_c 选为拓扑隐藏相变点）：

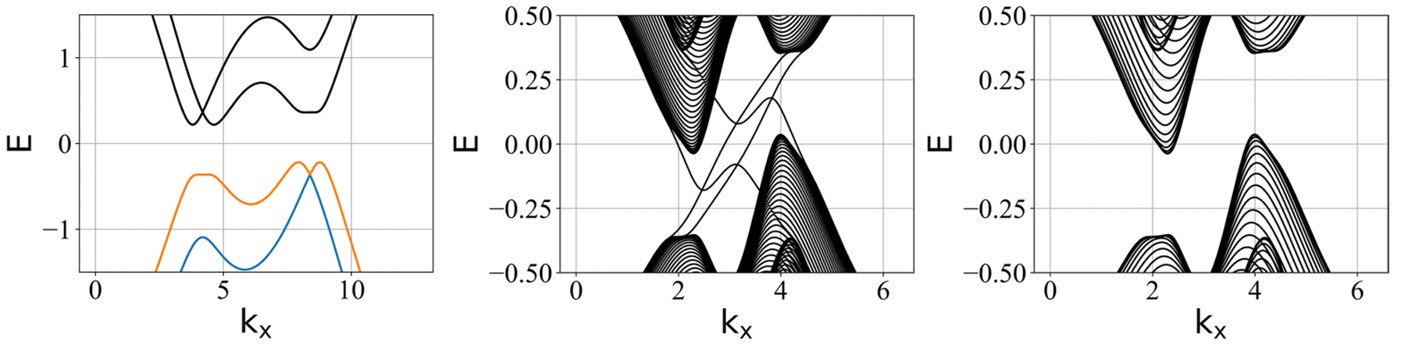
可以发现，当次近邻跃迁强度 t₂ 比较大时，发生拓扑隐藏相变点时，条带的能带结构中体带隙还未完全打开，但这个偏差并不影响本篇文章的主要结论，这是因为：（1）当探测到 2e²/h 电导平台，系统必然已经发生拓扑隐藏相变。（2）次近邻跃迁强度 t₂ 的值一般比较小，因此拓扑隐藏相变和 2e²/h 电导平台的探测基本上保持一致性。

5. 更多内容

不同堆垛方式的影响：

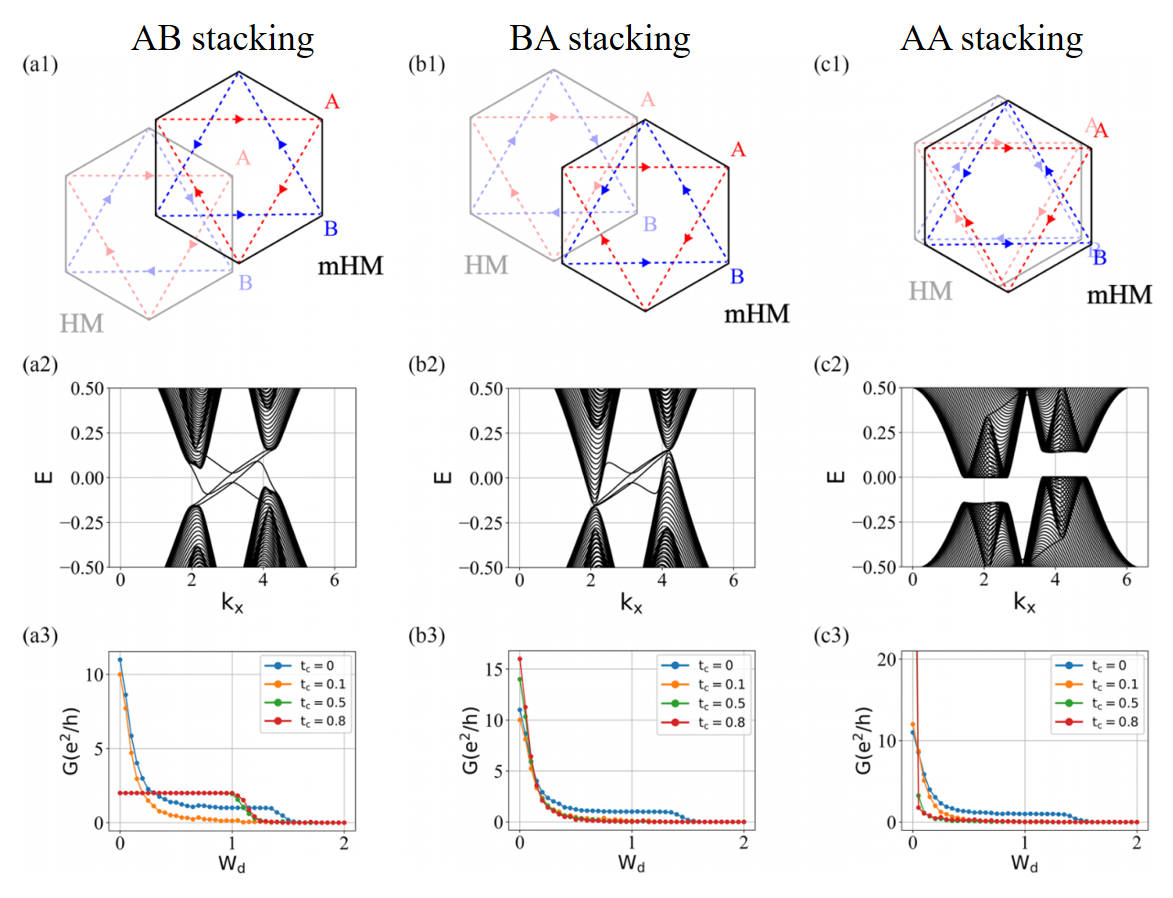
通过量子点接触 (quantum point contact) 电调控半反手性边缘态：

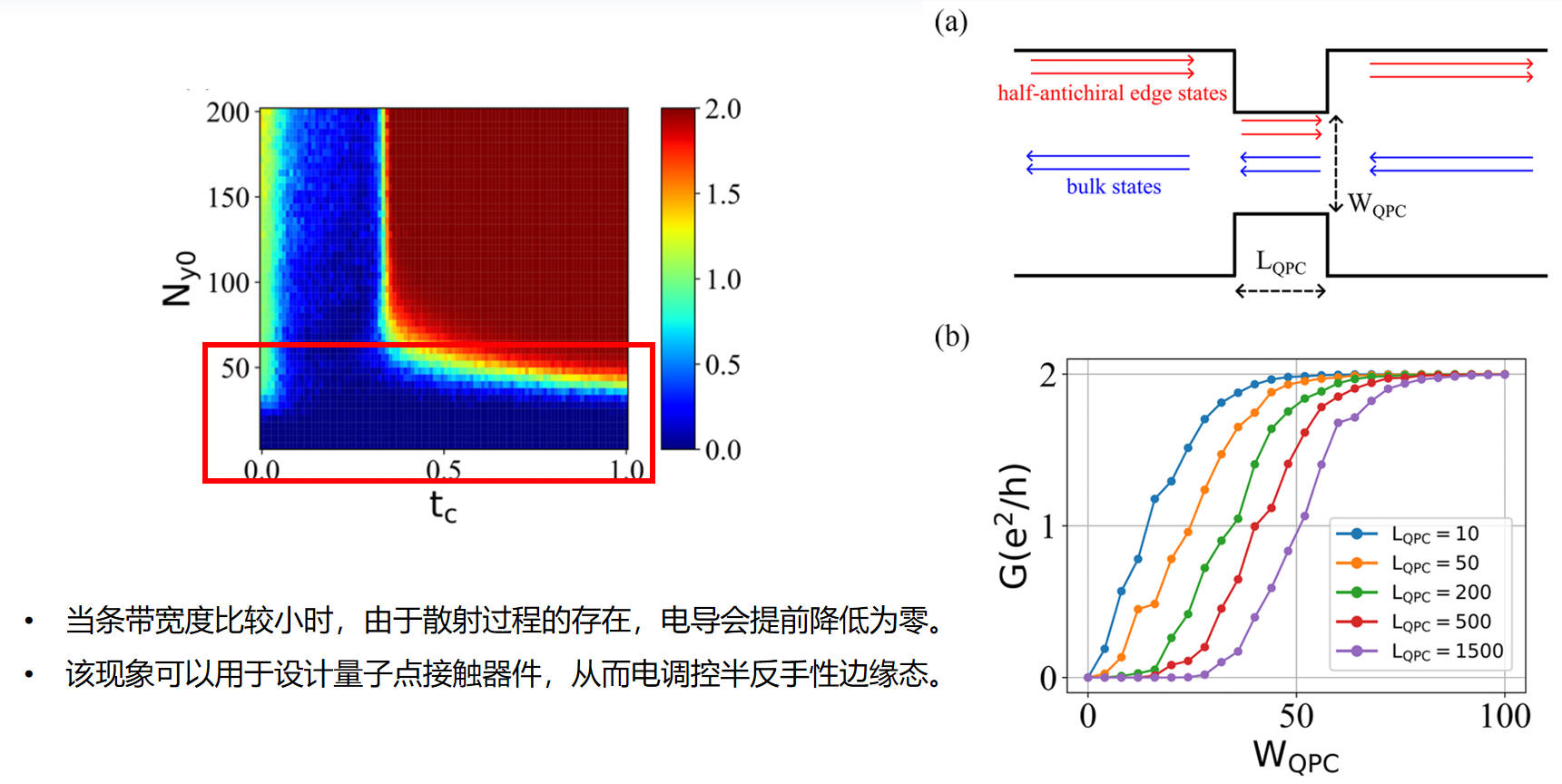
6. 总结

随着层间耦合强度的增加，半反手性边缘态（half-antichiral edge states）变得鲁棒，电导达到了 2e²/h 的平台，准一维的条带系统发生了从半金属态向拓扑绝缘态的转变。
在这个过程中，二维系统价带的内部同时也发生了“拓扑隐藏相变”（topological hidden phase transition），价带陈数由 C=±(1+1) 转变成 C=±(2+0)。
在这个复合蜂窝双层结构中，半反手性边缘态 2e²/h 的电导平台的出现可以作为拓扑隐藏相变的一个重要指标或测量方法。

7. 代码开源

这里开源主要的实现代码。更多的代码未整理，暂不开源，如果需要更多代码，可联系我。

代码一

import numpy as np
import functools
from math import *
import cmath
import guan

# Installation: pip install --upgrade guan

def main():
    N = 15
    M = 0
    t1 = 1
    phi= pi/2
    t2= 0.03
    tc = 0.8
    layer_num = 2
    bands_of_bilayer_model(N, M, t1, t2, phi, tc, layer_num)
    conductance_of_bilayer_model_with_disorder_array(N, M, t1, t2, phi, tc, layer_num)

# Haldane model

def hamiltonian_of_Haldane_model(k, N, M, t1, t2, phi, sign):
    h00 = h00_of_Haldane_model(N, M, t1, t2, phi, sign)
    h01 = h01_of_Haldane_model(N, M, t1, t2, phi, sign)
    hamiltonian = h00 + h01*cmath.exp(1j*k) + h01.transpose().conj()*cmath.exp(-1j*k)
    return hamiltonian

def h00_of_Haldane_model(N, M, t1, t2, phi, sign):
    h00 = np.zeros((4*N, 4*N), dtype=complex)
    for i0 in range(N):
        h00[i0*4+0, i0*4+0] = M
        h00[i0*4+1, i0*4+1] = -M
        h00[i0*4+2, i0*4+2] = M
        h00[i0*4+3, i0*4+3] = -M
        h00[i0*4+0, i0*4+1] = t1
        h00[i0*4+1, i0*4+0] = t1
        h00[i0*4+1, i0*4+2] = t1
        h00[i0*4+2, i0*4+1] = t1
        h00[i0*4+2, i0*4+3] = t1
        h00[i0*4+3, i0*4+2] = t1
        h00[i0*4+0, i0*4+2] = t2*cmath.exp(1j*phi*sign)
        h00[i0*4+2, i0*4+0] = h00[i0*4+0, i0*4+2].conj()
        h00[i0*4+1, i0*4+3] = t2*cmath.exp(1j*phi*sign)
        h00[i0*4+3, i0*4+1] = h00[i0*4+1, i0*4+3].conj()
    for i0 in range(N-1):
        h00[i0*4+3, (i0+1)*4+0] = t1
        h00[(i0+1)*4+0, i0*4+3] = t1
        h00[i0*4+2, (i0+1)*4+0] = t2*cmath.exp(-1j*phi*sign)
        h00[(i0+1)*4+0, i0*4+2] = h00[i0*4+2, (i0+1)*4+0].conj()
        h00[i0*4+3, (i0+1)*4+1] = t2*cmath.exp(-1j*phi*sign)
        h00[(i0+1)*4+1, i0*4+3] = h00[i0*4+3, (i0+1)*4+1].conj()
    return h00

def h01_of_Haldane_model(N, M, t1, t2, phi, sign):
    h01 = np.zeros((4*N, 4*N), dtype=complex)
    for i0 in range(N):
        h01[i0*4+1, i0*4+0] = t1
        h01[i0*4+2, i0*4+3] = t1
        h01[i0*4+0, i0*4+0] = t2*cmath.exp(-1j*phi*sign)
        h01[i0*4+1, i0*4+1] = t2*cmath.exp(1j*phi*sign)
        h01[i0*4+2, i0*4+2] = t2*cmath.exp(-1j*phi*sign)
        h01[i0*4+3, i0*4+3] = t2*cmath.exp(1j*phi*sign)
        h01[i0*4+1, i0*4+3] = t2*cmath.exp(-1j*phi*sign)
        h01[i0*4+2, i0*4+0] = t2*cmath.exp(1j*phi*sign)
        if i0 != 0:
            h01[i0*4+1, (i0-1)*4+3] = t2*cmath.exp(-1j*phi*sign)
    for i0 in range(N-1):
        h01[i0*4+2, (i0+1)*4+0] = t2*cmath.exp(1j*phi*sign)
    return h01

# modified_Haldane_model

def hamiltonian_of_modified_Haldane_model(k, N, M, t1, t2, phi, sign):
    h00 = h00_of_modified_Haldane_model(N, M, t1, t2, phi, sign)
    h01 = h01_of_modified_Haldane_model(N, M, t1, t2, phi, sign)
    hamiltonian = h00 + h01*cmath.exp(1j*k) + h01.transpose().conj()*cmath.exp(-1j*k)
    return hamiltonian

def h00_of_modified_Haldane_model(N, M, t1, t2, phi, sign):
    h00 = np.zeros((4*N, 4*N), dtype=complex)
    for i0 in range(N):
        h00[i0*4+0, i0*4+0] = M
        h00[i0*4+1, i0*4+1] = -M
        h00[i0*4+2, i0*4+2] = M
        h00[i0*4+3, i0*4+3] = -M
        h00[i0*4+0, i0*4+1] = t1
        h00[i0*4+1, i0*4+0] = t1
        h00[i0*4+1, i0*4+2] = t1
        h00[i0*4+2, i0*4+1] = t1
        h00[i0*4+2, i0*4+3] = t1
        h00[i0*4+3, i0*4+2] = t1
        h00[i0*4+0, i0*4+2] = t2*cmath.exp(-1j*phi*sign)
        h00[i0*4+2, i0*4+0] = h00[i0*4+0, i0*4+2].conj()
        h00[i0*4+1, i0*4+3] = t2*cmath.exp(1j*phi*sign)
        h00[i0*4+3, i0*4+1] = h00[i0*4+1, i0*4+3].conj()
    for i0 in range(N-1):
        h00[i0*4+3, (i0+1)*4+0] = t1
        h00[(i0+1)*4+0, i0*4+3] = t1
        h00[i0*4+2, (i0+1)*4+0] = t2*cmath.exp(1j*phi*sign)
        h00[(i0+1)*4+0, i0*4+2] = h00[i0*4+2, (i0+1)*4+0].conj()
        h00[i0*4+3, (i0+1)*4+1] = t2*cmath.exp(-1j*phi*sign)
        h00[(i0+1)*4+1, i0*4+3] = h00[i0*4+3, (i0+1)*4+1].conj()
    return h00

def h01_of_modified_Haldane_model(N, M, t1, t2, phi, sign):
    h01 = np.zeros((4*N, 4*N), dtype=complex)
    for i0 in range(N):
        h01[i0*4+1, i0*4+0] = t1
        h01[i0*4+2, i0*4+3] = t1
        h01[i0*4+0, i0*4+0] = t2*cmath.exp(1j*phi*sign)
        h01[i0*4+1, i0*4+1] = t2*cmath.exp(1j*phi*sign)
        h01[i0*4+2, i0*4+2] = t2*cmath.exp(1j*phi*sign)
        h01[i0*4+3, i0*4+3] = t2*cmath.exp(1j*phi*sign)
        h01[i0*4+1, i0*4+3] = t2*cmath.exp(-1j*phi*sign)
        h01[i0*4+2, i0*4+0] = t2*cmath.exp(-1j*phi*sign)
        if i0 != 0:
            h01[i0*4+1, (i0-1)*4+3] = t2*cmath.exp(-1j*phi*sign)
    for i0 in range(N-1):
        h01[i0*4+2, (i0+1)*4+0] = t2*cmath.exp(-1j*phi*sign)
    return h01

# bilayer model

def hamiltonian_of_bilayer_model(k, N, M, t1, t2, phi, tc, layer_num):
    modified_Haldane_model = hamiltonian_of_modified_Haldane_model(k=k, N=N, M=M, t1=t1, t2=t2, phi=phi, sign=1)
    Haldane_model = hamiltonian_of_Haldane_model(k=k, N=N, M=M, t1=t1, t2=t2, phi=phi, sign=1)
    hamiltonian = np.zeros((4*N*layer_num, 4*N*layer_num), dtype=complex)
    for layer in range(layer_num):
        if np.mod(layer,2) == 0:
            hamiltonian[layer*4*N+0:layer*4*N+4*N, layer*4*N+0:layer*4*N+4*N] = modified_Haldane_model
        if np.mod(layer,2) == 1:
            hamiltonian[layer*4*N+0:layer*4*N+4*N, layer*4*N+0:layer*4*N+4*N] = Haldane_model 
    for layer in range(layer_num-1):
        for i0 in range(N):
            # AB stacking
            hamiltonian[layer*4*N+i0*4+0, (layer+1)*4*N+i0*4+1] = tc
            hamiltonian[(layer+1)*4*N+i0*4+1, layer*4*N+i0*4+0] = tc
            hamiltonian[layer*4*N+i0*4+2, (layer+1)*4*N+i0*4+3] = tc
            hamiltonian[(layer+1)*4*N+i0*4+3, layer*4*N+i0*4+2] = tc
            
            # # # BA stacking
            # hamiltonian[layer*4*N+i0*4+1, (layer+1)*4*N+i0*4+0] = tc
            # hamiltonian[(layer+1)*4*N+i0*4+0, layer*4*N+i0*4+1] = tc
            # hamiltonian[layer*4*N+i0*4+3, (layer+1)*4*N+i0*4+2] = tc
            # hamiltonian[(layer+1)*4*N+i0*4+2, layer*4*N+i0*4+3] = tc

            # # AA stacking
            # hamiltonian[layer*4*N+i0*4+0, (layer+1)*4*N+i0*4+0] = tc
            # hamiltonian[(layer+1)*4*N+i0*4+0, layer*4*N+i0*4+0] = tc
            # hamiltonian[layer*4*N+i0*4+1, (layer+1)*4*N+i0*4+1] = tc
            # hamiltonian[(layer+1)*4*N+i0*4+1, layer*4*N+i0*4+1] = tc
            # hamiltonian[layer*4*N+i0*4+2, (layer+1)*4*N+i0*4+2] = tc
            # hamiltonian[(layer+1)*4*N+i0*4+2, layer*4*N+i0*4+2] = tc
            # hamiltonian[layer*4*N+i0*4+3, (layer+1)*4*N+i0*4+3] = tc
            # hamiltonian[(layer+1)*4*N+i0*4+3, layer*4*N+i0*4+3] = tc
    return hamiltonian

def h00_of_bilayer_model(N, M, t1, t2, phi, tc, layer_num):
    h00_modified = h00_of_modified_Haldane_model(N, M, t1, t2, phi, sign=1)
    h00_Haldane = h00_of_Haldane_model(N, M, t1, t2, phi, sign=1)
    h00  = np.zeros((4*N*layer_num, 4*N*layer_num), dtype=complex) 
    for layer in range(layer_num):
        if np.mod(layer,2) == 0:
            h00[layer*4*N+0:layer*4*N+4*N, layer*4*N+0:layer*4*N+4*N] = h00_modified
        if np.mod(layer,2) == 1:
            h00[layer*4*N+0:layer*4*N+4*N, layer*4*N+0:layer*4*N+4*N] = h00_Haldane
    for layer in range(layer_num-1):
        for i0 in range(N):
            # AB stacking
            h00[layer*4*N+i0*4+0, (layer+1)*4*N+i0*4+1] = tc
            h00[(layer+1)*4*N+i0*4+1, layer*4*N+i0*4+0] = tc
            h00[layer*4*N+i0*4+2, (layer+1)*4*N+i0*4+3] = tc
            h00[(layer+1)*4*N+i0*4+3, layer*4*N+i0*4+2] = tc

            # # BA stacking
            # h00[layer*4*N+i0*4+1, (layer+1)*4*N+i0*4+0] = tc
            # h00[(layer+1)*4*N+i0*4+0, layer*4*N+i0*4+1] = tc
            # h00[layer*4*N+i0*4+3, (layer+1)*4*N+i0*4+2] = tc
            # h00[(layer+1)*4*N+i0*4+2, layer*4*N+i0*4+3] = tc

            # # AA stacking
            # h00[layer*4*N+i0*4+0, (layer+1)*4*N+i0*4+0] = tc
            # h00[(layer+1)*4*N+i0*4+0, layer*4*N+i0*4+0] = tc
            # h00[layer*4*N+i0*4+1, (layer+1)*4*N+i0*4+1] = tc
            # h00[(layer+1)*4*N+i0*4+1, layer*4*N+i0*4+1] = tc
            # h00[layer*4*N+i0*4+2, (layer+1)*4*N+i0*4+2] = tc
            # h00[(layer+1)*4*N+i0*4+2, layer*4*N+i0*4+2] = tc
            # h00[layer*4*N+i0*4+3, (layer+1)*4*N+i0*4+3] = tc
            # h00[(layer+1)*4*N+i0*4+3, layer*4*N+i0*4+3] = tc
    return h00

def h01_of_bilayer_model(N, M, t1, t2, phi, tc, layer_num):
    h01_modified = h01_of_modified_Haldane_model(N, M, t1, t2, phi, sign=1)
    h01_Haldane = h01_of_Haldane_model(N, M, t1, t2, phi, sign=1)
    h01  = np.zeros((4*N*layer_num, 4*N*layer_num), dtype=complex)
    for layer in range(layer_num):
        if np.mod(layer,2) == 0:
            h01[layer*4*N+0:layer*4*N+4*N, layer*4*N+0:layer*4*N+4*N] = h01_modified
        if np.mod(layer,2) == 1:
            h01[layer*4*N+0:layer*4*N+4*N, layer*4*N+0:layer*4*N+4*N] = h01_Haldane
    return h01

def bands_of_bilayer_model(N, M, t1, t2, phi, tc, layer_num):
    k_array = np.linspace(0, 2*pi, 300)
    hamiltonian = functools.partial(hamiltonian_of_bilayer_model, N=N, M=M, t1=t1, t2=t2, phi=phi, tc=tc, layer_num=layer_num)
    eigenvalue_array = guan.calculate_eigenvalue_with_one_parameter(k_array, hamiltonian, print_show=1)
    plt, fig, ax = guan.import_plt_and_start_fig_ax(labelsize=25)
    guan.plot_without_starting_fig_ax(plt, fig, ax, k_array, eigenvalue_array, xlabel='$\mathrm{k_x}$', ylabel='$\mathrm{E}$', style='k', fontsize=30,  y_max=0.2, y_min=-0.2,linewidth=None, markersize=None, color=None, fontfamily='Times New Roman')
    plt.show()

def conductance_of_bilayer_model_with_disorder_array(N, M, t1, t2, phi, tc, layer_num):
    h00 = h00_of_bilayer_model(N, M, t1, t2, phi, tc, layer_num)
    h01 = h01_of_bilayer_model(N, M, t1, t2, phi, tc, layer_num)
    fermi_energy = 0
    disorder_intensity_array = np.arange(0, 2.5, .05)
    conductance_array = guan.calculate_conductance_with_disorder_intensity_array(fermi_energy, h00, h01, disorder_intensity_array, length=100, calculation_times=3, print_show=1) # length=2000, calculation_times=20
    guan.plot(disorder_intensity_array, conductance_array, xlabel='$\mathrm{W_d}$', ylabel='$\mathrm{G(e^2/h)}$', style='o-')

if __name__ == '__main__':
    main()

代码二

import numpy as np
from math import *
import cmath
import functools
import guan 

# Installation: pip install --upgrade guan

def main():
    M = 0
    t1 = 1
    phi= pi/2
    t2 = 0.03
    tc = 0.31
    bilayer_bands(M, t1, t2, phi, tc)
    chern_number(M, t1, t2, phi)

def hamiltonian_of_Haldane(k1, k2, M, t1, t2, phi, a=1/sqrt(3)): 
    h0 = np.zeros((2, 2), dtype=complex)
    h1 = np.zeros((2, 2), dtype=complex)
    h2 = np.zeros((2, 2), dtype=complex)

    h1[1, 0] = t1*(cmath.exp(1j*k2*a)+cmath.exp(1j*sqrt(3)/2*k1*a-1j/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j/2*k2*a))
    h1[0, 1] = h1[0, 1].conj()

    h2[0, 0] = t2*cmath.exp(1j*phi)*(cmath.exp(1j*sqrt(3)*k1*a)+cmath.exp(-1j*sqrt(3)/2*k1*a+1j*3/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a))
    h2[1, 1] = t2*cmath.exp(-1j*phi)*(cmath.exp(1j*sqrt(3)*k1*a)+cmath.exp(-1j*sqrt(3)/2*k1*a+1j*3/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a))
    matrix = h0 + h1 + h2 + h2.transpose().conj()
    return matrix

def hamiltonian_of_modified_Haldane(k1, k2, M, t1, t2, phi, a=1/sqrt(3)): 
    h0 = np.zeros((2, 2), dtype=complex)
    h1 = np.zeros((2, 2), dtype=complex)
    h2 = np.zeros((2, 2), dtype=complex)

    k1 = -k1  # kx  # Note that to get the unit cell the bilayer honeycomb lattice containing all possible layer hoppings, here one layer (HM layer or mHM layer） needs to be applied with its counterpart of mirror symmetry along x direction.

    h1[1, 0] = t1*(cmath.exp(1j*k2*a)+cmath.exp(1j*sqrt(3)/2*k1*a-1j/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j/2*k2*a))
    h1[0, 1] = h1[1, 0].conj()

    h2[0, 0] = t2*cmath.exp(1j*phi)*(cmath.exp(1j*sqrt(3)*k1*a)+cmath.exp(-1j*sqrt(3)/2*k1*a+1j*3/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a))
    h2[1, 1] = t2*cmath.exp(1j*phi)*(cmath.exp(1j*sqrt(3)*k1*a)+cmath.exp(-1j*sqrt(3)/2*k1*a+1j*3/2*k2*a)+cmath.exp(-1j*sqrt(3)/2*k1*a-1j*3/2*k2*a))

    matrix = h0 + h1 + h2 + h2.transpose().conj()
    return matrix

def hamiltonian_of_bilayer(k1, k2, M, t1, t2, phi, tc):
    hamiltonian1 = hamiltonian_of_Haldane(k1, k2, M, t1, t2, phi, a=1/sqrt(3))
    hamiltonian2 = hamiltonian_of_modified_Haldane(k1, k2, M, t1, t2, phi, a=1/sqrt(3))
    hamiltonian = np.zeros((4, 4), dtype=complex)
    hamiltonian[0:2, 0:2] = hamiltonian1
    hamiltonian[2:4, 2:4] = hamiltonian2

    # AB stacking
    hamiltonian[1, 2] = tc   # B on HM， A on mHM
    hamiltonian[2, 1] = tc

    # BA stacking
    # hamiltonian[0, 3] = tc  # A on HM， B on mHM
    # hamiltonian[3, 0] = tc

    # AA stacking
    # hamiltonian[0, 2] = tc
    # hamiltonian[2, 0] = tc
    # hamiltonian[1, 3] = tc
    # hamiltonian[3, 1] = tc
    return hamiltonian

def bilayer_bands(M, t1, t2, phi, tc):
    k1_array = np.linspace(0, 4*pi, 3000)
    k2 = 0
    hamiltonian = functools.partial(hamiltonian_of_bilayer, k2=k2, M=M, t1=t1, t2=t2, phi=phi, tc=tc)
    eigenvalue_array = guan.calculate_eigenvalue_with_one_parameter(k1_array, hamiltonian)
    plt, fig, ax = guan.import_plt_and_start_fig_ax(labelsize=25)
    guan.plot_without_starting_fig_ax(plt, fig, ax, k1_array, eigenvalue_array[:, 0],  linewidth=2)
    guan.plot_without_starting_fig_ax(plt, fig, ax, k1_array, eigenvalue_array[:, 1],  linewidth=2)
    guan.plot_without_starting_fig_ax(plt, fig, ax, k1_array, eigenvalue_array[:, 2],  linewidth=2, color='k')
    guan.plot_without_starting_fig_ax(plt, fig, ax, k1_array, eigenvalue_array[:, 3],  linewidth=2, color='k')
    guan.plot_without_starting_fig_ax(plt, fig, ax, [], [], fontsize=30, y_max=1.5, y_min=-1.5, xlabel='$\mathrm{k_x}$', ylabel='$\mathrm{E}$')
    plt.show()

def chern_number(M, t1, t2, phi):
    tc_array = np.arange(0.05, 0.8, 0.05)
    chern_number_array = []
    for tc in tc_array:
        print(tc)
        hamiltonian = functools.partial(hamiltonian_of_bilayer, M=M, t1=t1, t2=t2, phi=phi, tc=tc)
        chern_number = guan.calculate_chern_number_for_honeycomb_lattice(hamiltonian, a=1/sqrt(3), precision=500, print_show=0)
        print(chern_number, '\n')
        chern_number_array.append(chern_number[0:2])
    guan.plot(tc_array, np.real(chern_number_array), xlabel='$\mathrm{t_c}$', ylabel='$\mathrm{C}$', style='o-')

if __name__ == '__main__':
    main()

299 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】

高陈数的蜂窝双层系统中的拓扑隐藏相变 Topological hidden phase transition in honeycomb bilayers with a high Chern number

原文

摘要

1. 主要研究背景