不同取点数量的画图视觉效果

本篇给出相对连续光滑的函数在不同取点数量下的画图视觉效果，仅供参考，具体的取点数量应该以实际数据作为考量。

这里以 Sigmoid 函数为例：

$\mathrm{Sigmoid}(x)=\frac{1}{1+\mathrm{exp}(-x)}$

主要结论为：

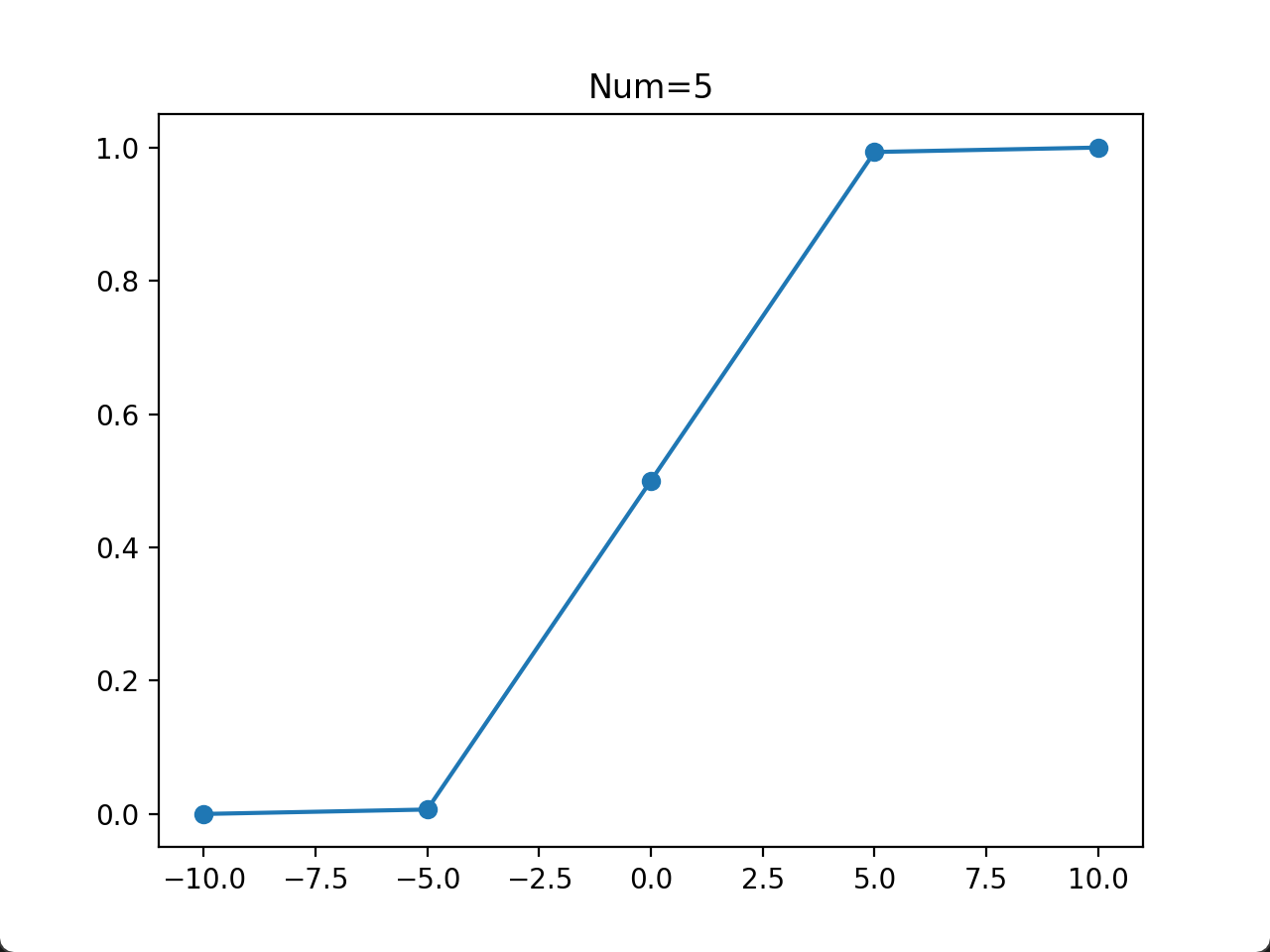
当取点数量为 5 左右时，还不能完全描述函数的性质。在计算/实验成本比较高的情况下，且数据理论上是线性的，才可以取 5 这个数量。
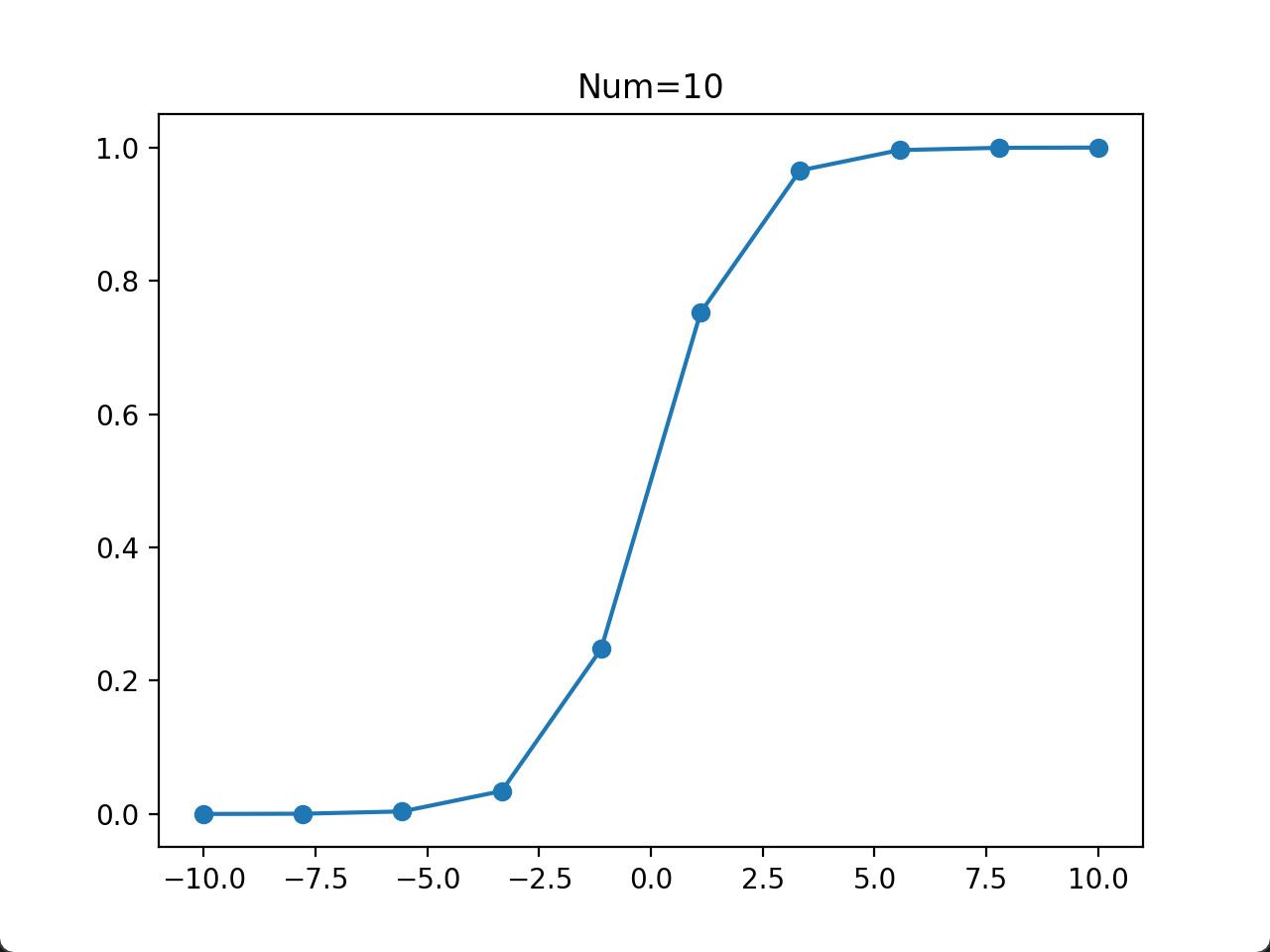
当取点数量为 10 左右时，大致能看出函数形状，但不是很光滑。在计算/实验成本比较高的情况下，取 10 个点也是勉强可行的。
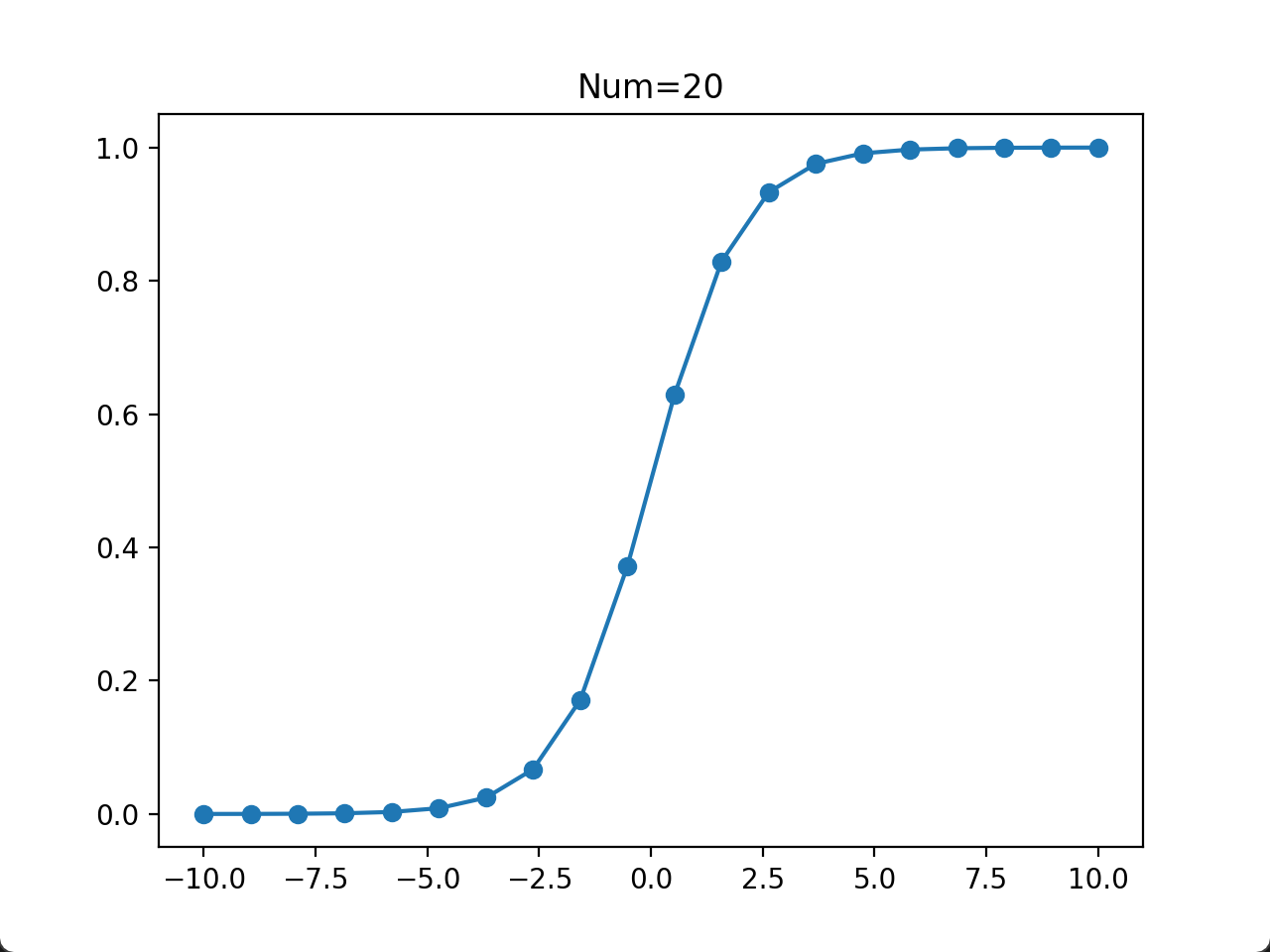
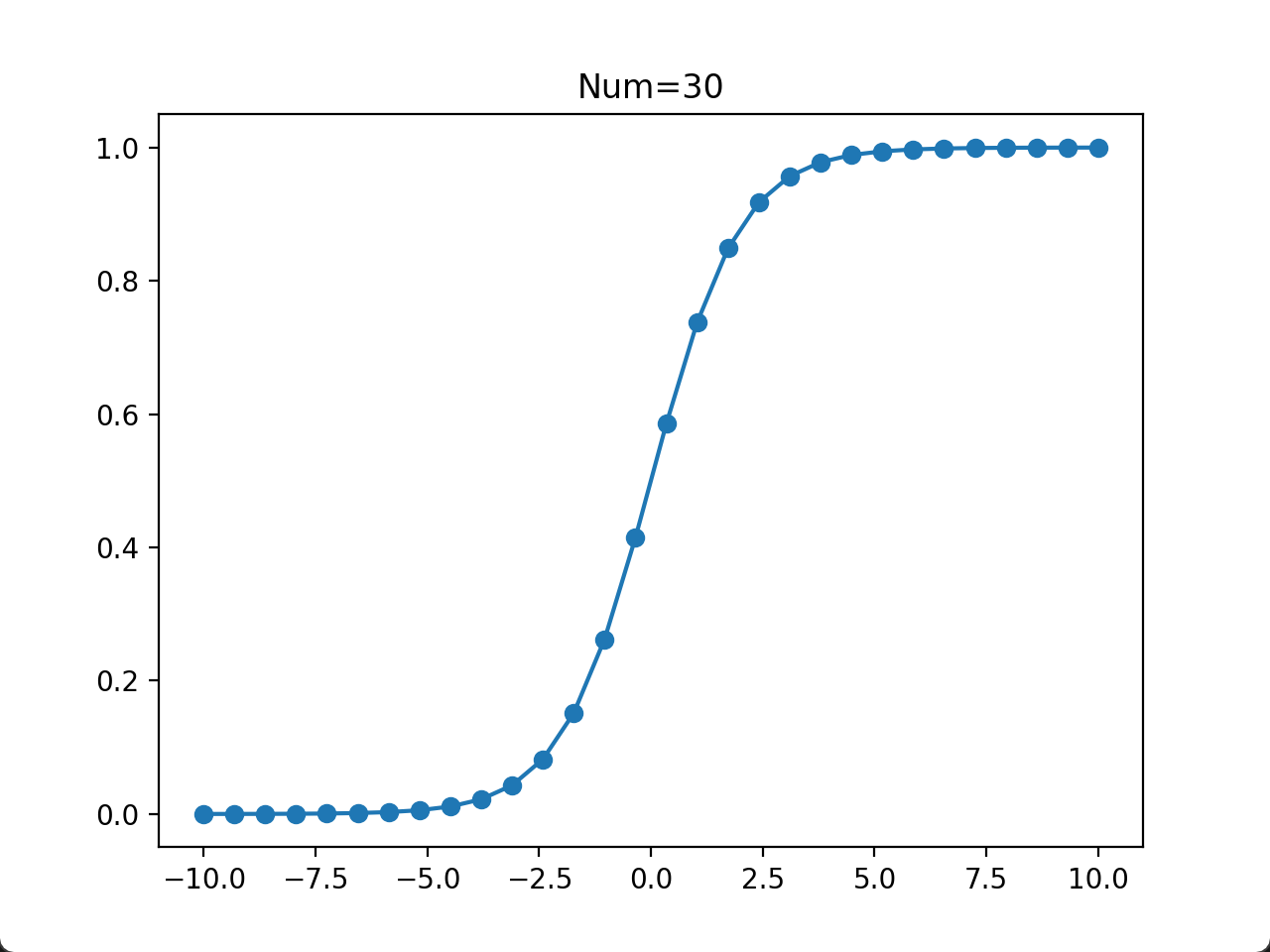
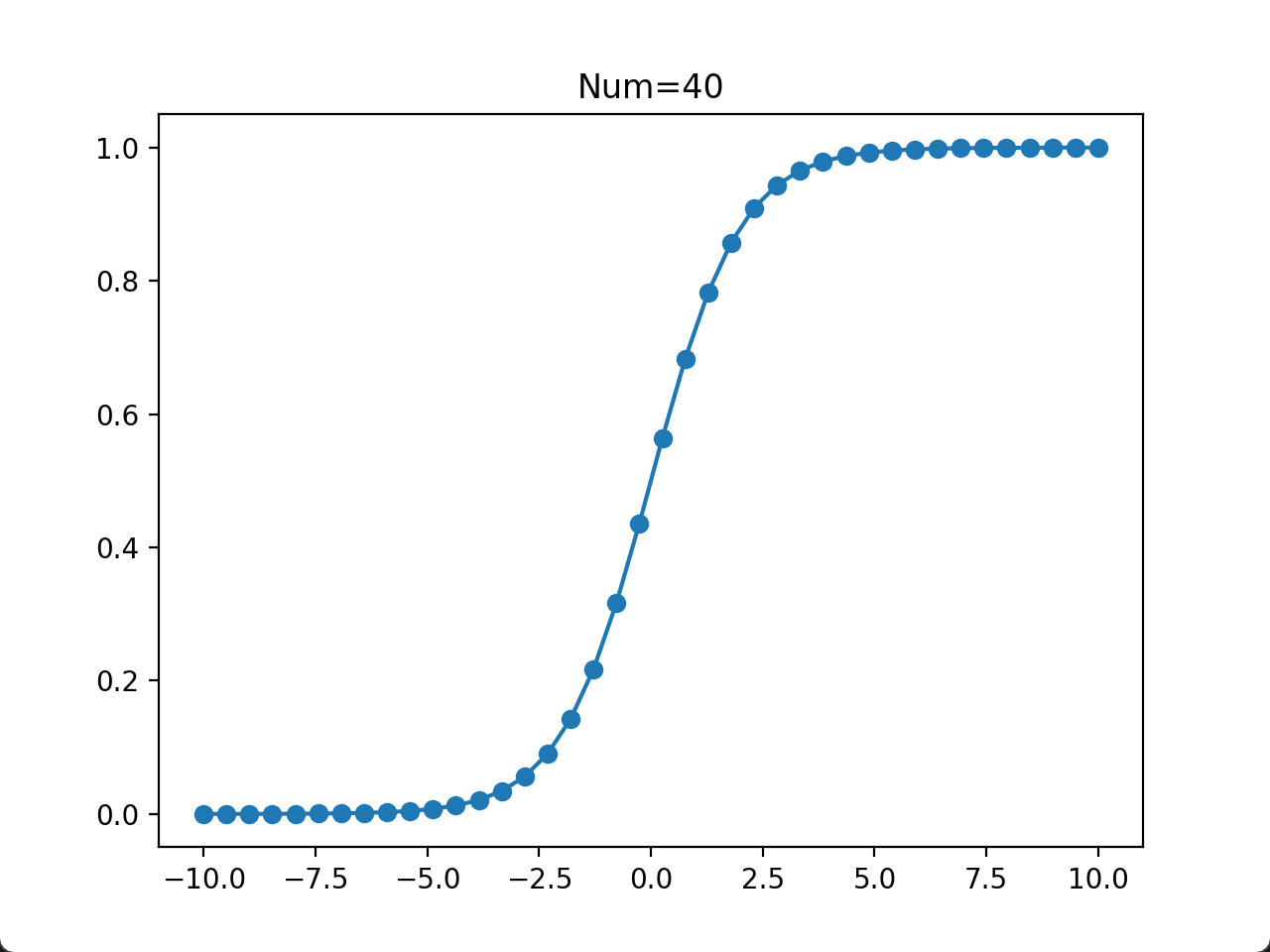
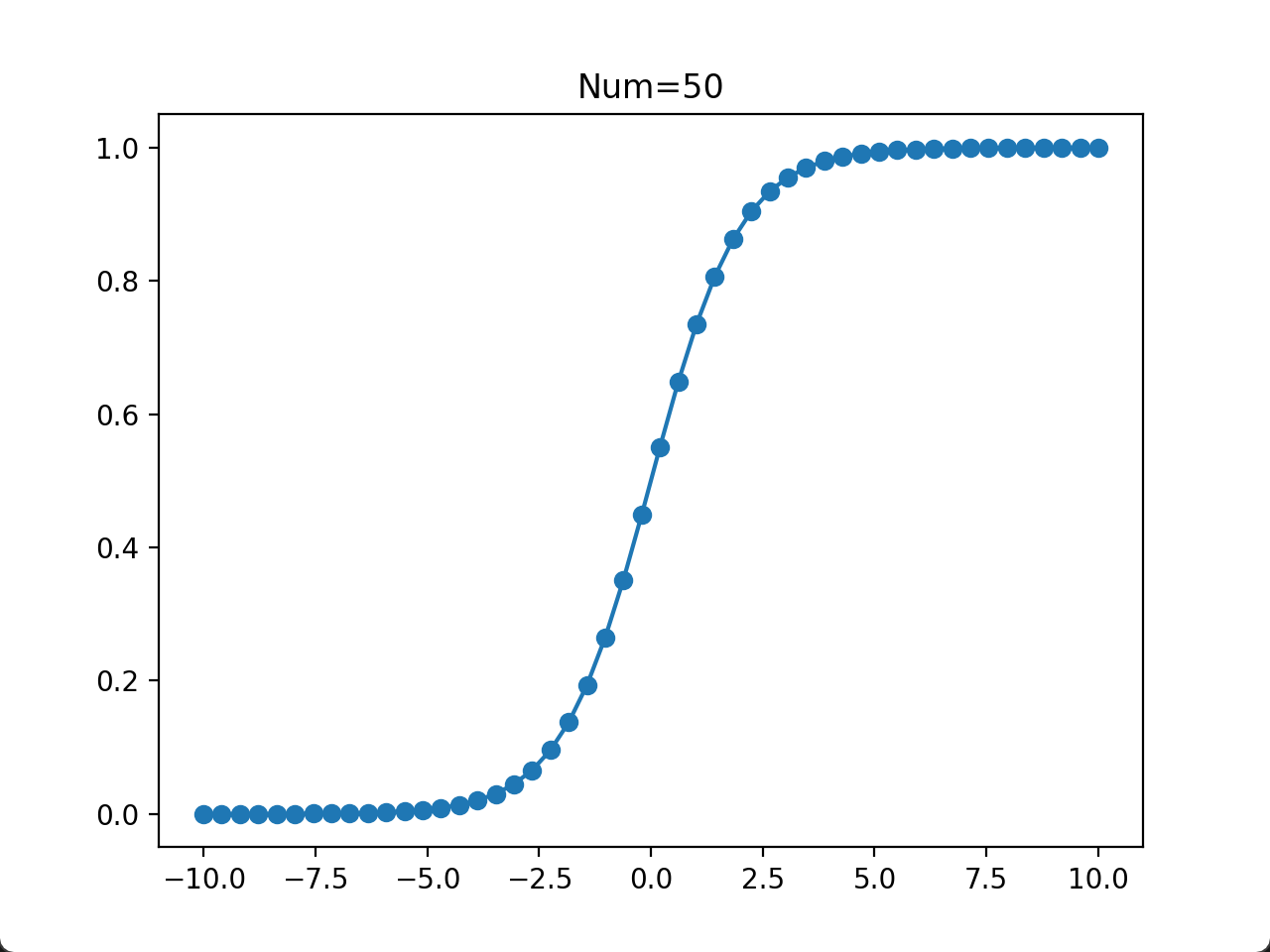
当取点数量为 20~100 时，基本上可以说明问题了。在计算/实验成本比较高的情况下，推荐数据的取点数量为这个区间，例如取点数量为 30。
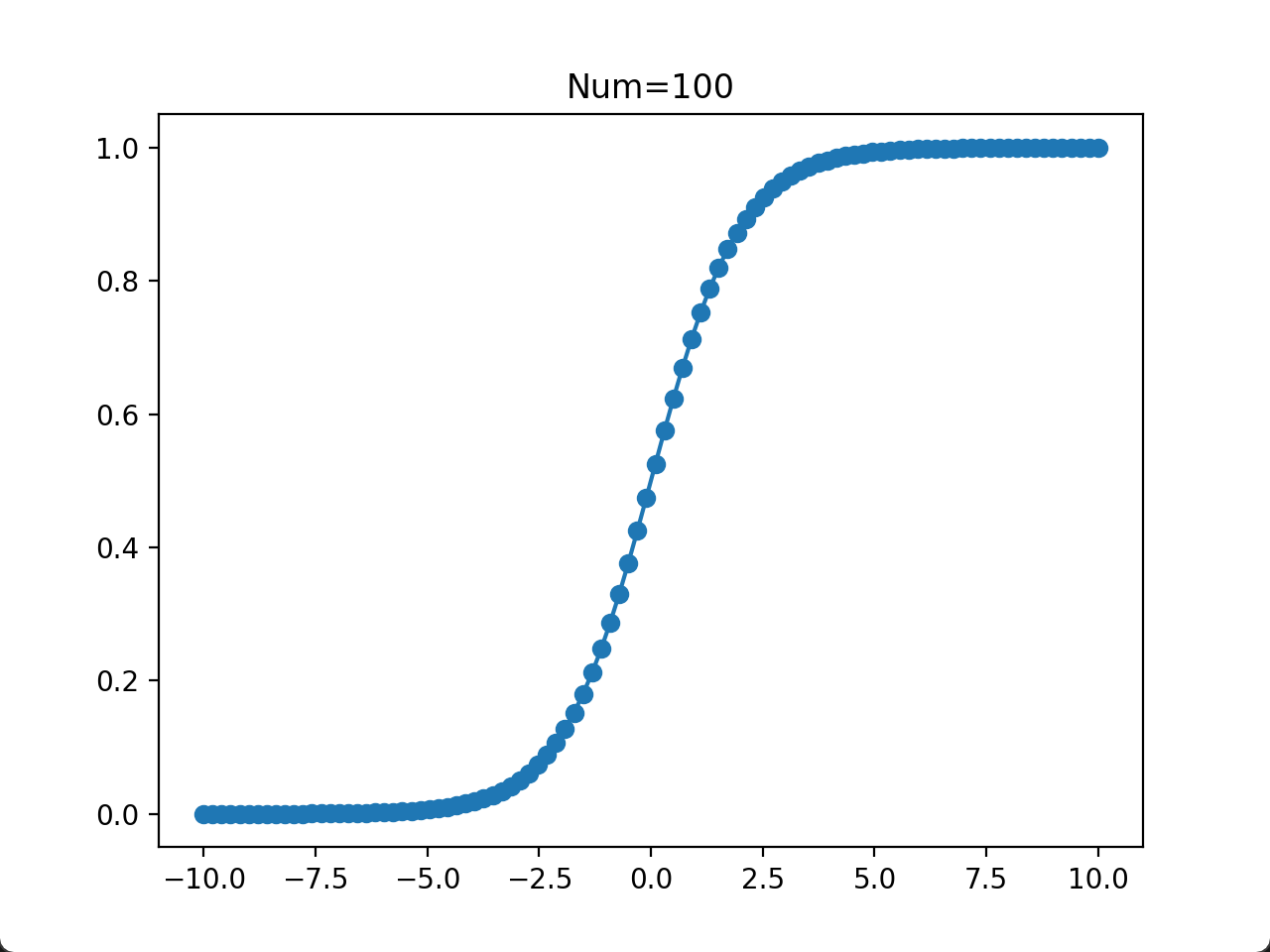
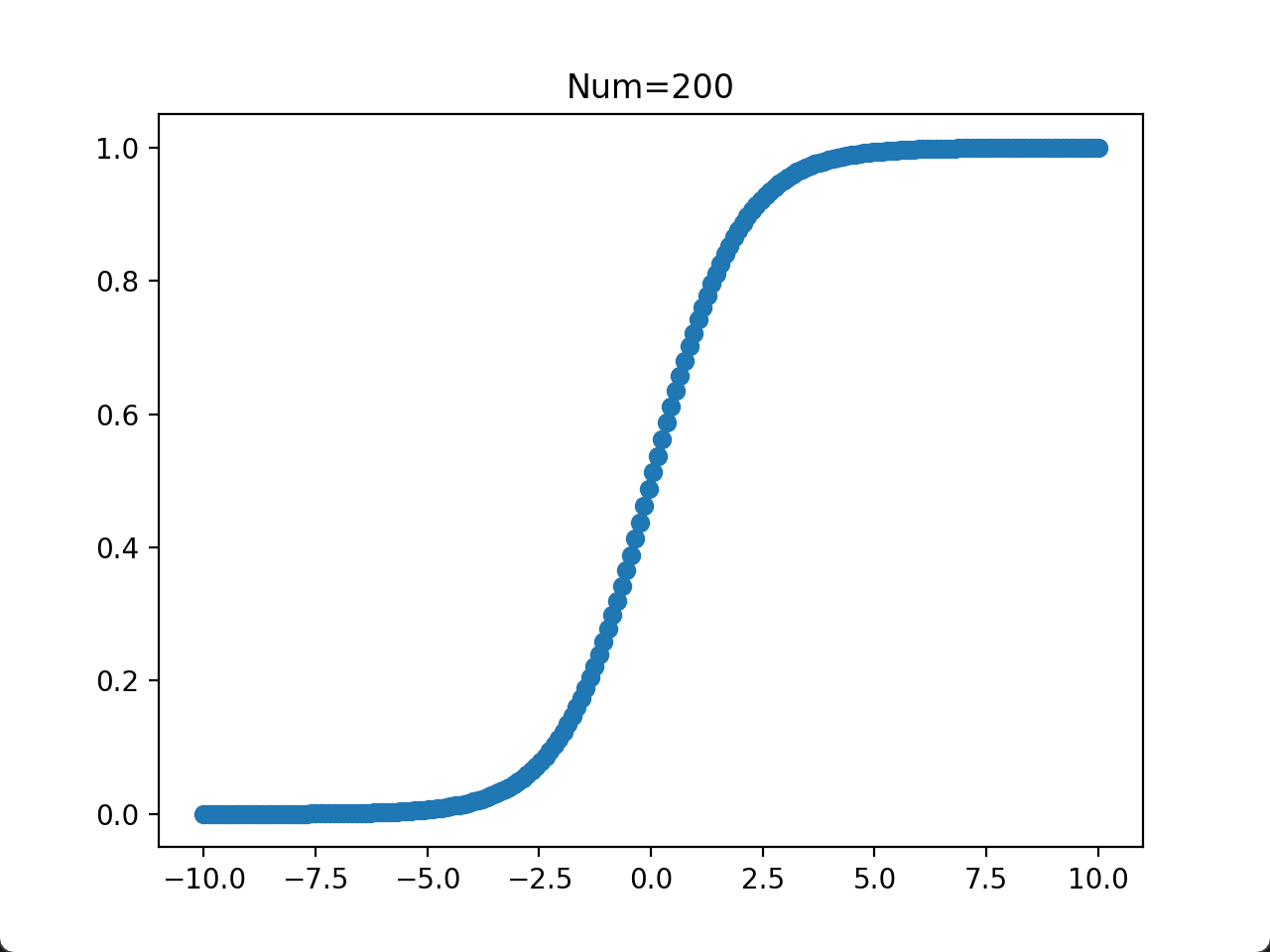
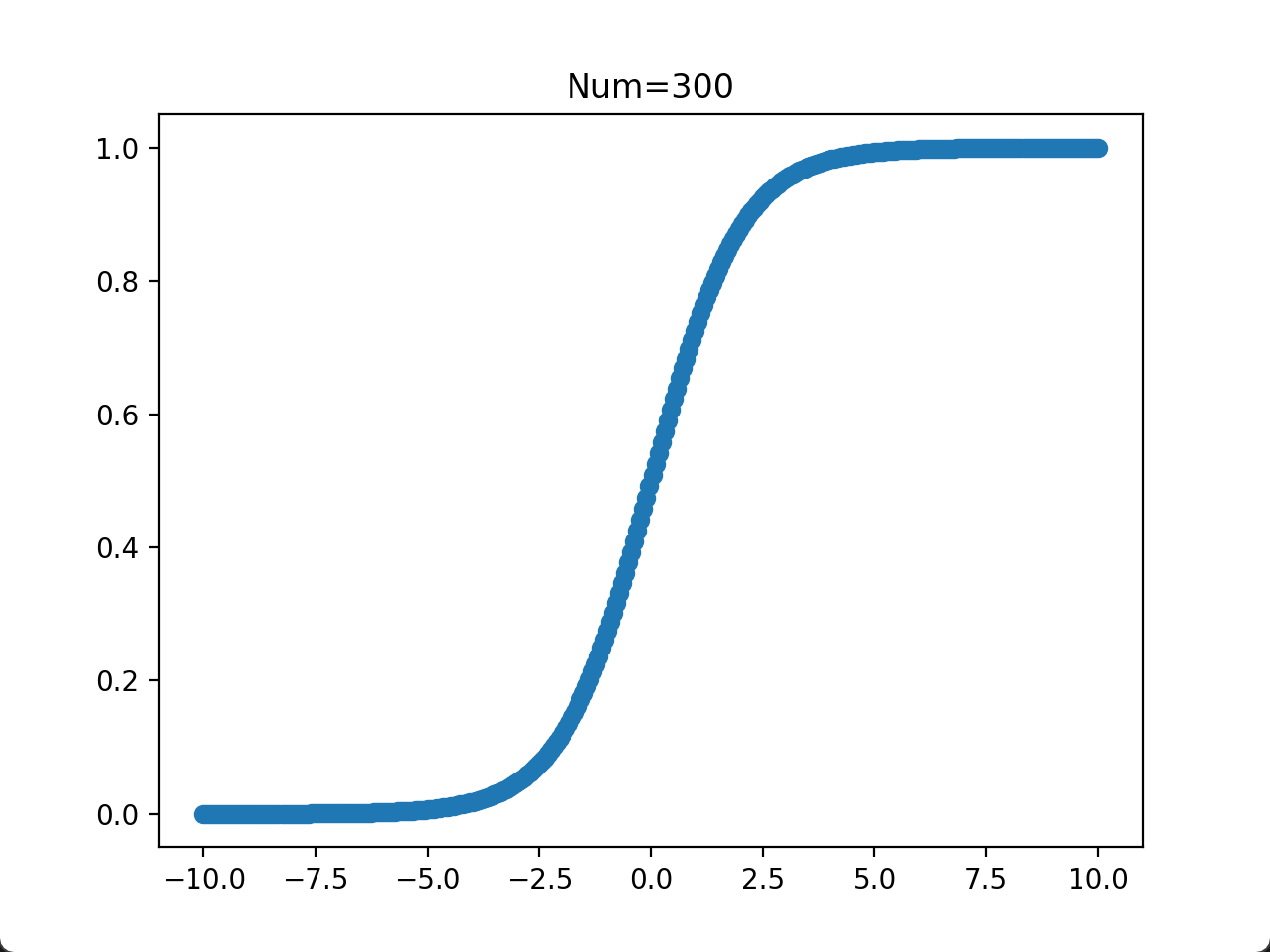
当取点数量为 100~300 时，大部分的取点已经连在一起了。在计算/实验成本比较低的情况下，数据的取点数量可以在这个区间。
另外，如果函数是剧烈波动，那么总的取点数量可能需要超过 300，或者是在局部剧烈波动的地方取点比较密。

画图的 Python 代码为：

import numpy as np
import matplotlib.pyplot as plt

def sigmoid_function(x):
    y = 1/(1+np.exp(-x))
    return y

for num in [10, 20, 30, 40, 50, 60, 100, 200, 300]:
    x_array = np.linspace(-10, 10, num)
    y_array = []
    for x in x_array:
        y = sigmoid_function(x)
        y_array.append(y)
    plt.plot(x_array, y_array, 'o-')
    plt.title(f'Num={num}')
    plt.show()

运行结果：