一个实空间拓扑不变量的公式推导（local Chern marker）

本篇的主要参考文献：Mapping topological order in coordinate space。

陈数的定义公式如下，可参考这篇：陈数Chern number的计算（定义法，附Python/Matlab代码）。

$C_n=\frac{1}{2\pi i} \int_{T^2} d^2 k F_{12}(k)$

通过转换可写成以下这个形式。可参考这篇的前半部分：陈数Chern number的计算（Kubo公式，附Python代码）。

$C=-\frac{1}{\pi} \mathrm{Im} \sum_{n=1}^{N_c}\int_{T^2} d\mathbf{k} \left\langle \frac{\partial }{\partial k_x} u_{n\mathbf{k}} \middle| \frac{\partial }{\partial k_y} u_{n\mathbf{k}} \right\rangle$

其中， $N_c$ 是占据态的能带数量。

插入单位算符后得到：

$C = -\frac{1}{\pi} \text{Im} \sum_{n=1}^{N_c} \sum_{n' = 1}^{\infty} \int_{\text{BZ}} d\mathbf{k} \, \left\langle \frac{\partial u_{n\mathbf{k}}}{\partial k_x} \middle| u_{n'\mathbf{k}} \right\rangle \left\langle u_{n'\mathbf{k}} \middle| \frac{\partial u_{n\mathbf{k}}}{\partial k_y} \right\rangle$

接下来详细考虑 $\sum_{n=1}^{N_c} \sum_{n' = 1}^{\infty}$ 中的每一项。

当 $n=n'$ 时，有（第一个等号是顺序交换；第二个等号是复数共轭）：

$\begin{aligned} \left\langle \frac{\partial u_{n\mathbf{k}}}{\partial k_x} \middle| u_{n\mathbf{k}} \right\rangle \left\langle u_{n\mathbf{k}} \middle| \frac{\partial u_{n\mathbf{k}}}{\partial k_y} \right\rangle &=\left\langle u_{n\mathbf{k}} \middle| \frac{\partial u_{n\mathbf{k}}}{\partial k_y} \right\rangle \left\langle \frac{\partial u_{n\mathbf{k}}}{\partial k_x} \middle| u_{n\mathbf{k}} \right\rangle \\& =\left( \left\langle \frac{\partial u_{n\mathbf{k}}}{\partial k_x} \middle| u_{n\mathbf{k}} \right\rangle \left\langle u_{n\mathbf{k}} \middle| \frac{\partial u_{n\mathbf{k}}}{\partial k_y} \right\rangle \right)^*\end{aligned}$

所以 $n=n'$ 这一项是实数，不贡献值，可扔掉。

当 $n \neq n'$ 时, 有 $\langle u_{n \mathbf{k}} | u_{n' \mathbf{k}} \rangle=0$ ，所以 $\frac{\partial}{\partial k_j}\langle u_{n \mathbf{k}} | u_{n' \mathbf{k}} \rangle=0$ ，展开得到：

$\left\langle \frac{\partial u_{n\mathbf{k}}}{\partial k_j} \middle| u_{n'\mathbf{k}} \right\rangle = - \left\langle u_{n\mathbf{k}} \middle| \frac{\partial u_{n'\mathbf{k}}}{\partial k_j} \right\rangle$

对于 $n=n_1$ , $n'=n_2 \in [1, N_c]$ ，在求和 $\sum_{n=1}^{N_c} \sum_{n' = 1}^{\infty}$ 中的表达式 $\left\langle \frac{\partial u_{n\mathbf{k}}}{\partial k_x} \middle| u_{n'\mathbf{k}} \right\rangle \left\langle u_{n'\mathbf{k}} \middle| \frac{\partial u_{n\mathbf{k}}}{\partial k_y} \right\rangle$ 都对应的 $n=n_2$ , $n'=n_1$ 项。这里把这两个对应项写在一块，并取虚数（第一个等号用到上面的等式替换，两个负号相互抵消；第二个等号用上厄密共轭的缩写）：

$\begin{aligned} & \mathrm{Im} \left( \left\langle \frac{\partial u_{n_1\mathbf{k}}}{\partial k_x} \middle| u_{n_2\mathbf{k}} \right\rangle \left\langle u_{n_2\mathbf{k}} \middle| \frac{\partial u_{n_1\mathbf{k}}}{\partial k_y} \right\rangle + \left\langle \frac{\partial u_{n_2\mathbf{k}}}{\partial k_x} \middle| u_{n_1\mathbf{k}} \right\rangle \left\langle u_{n_1\mathbf{k}} \middle| \frac{\partial u_{n_2\mathbf{k}}}{\partial k_y} \right\rangle \right)\\=& \mathrm{Im} \left( \left\langle \frac{\partial u_{n_1\mathbf{k}}}{\partial k_x} \middle| u_{n_2\mathbf{k}} \right\rangle \left\langle u_{n_2\mathbf{k}} \middle| \frac{\partial u_{n_1\mathbf{k}}}{\partial k_y} \right\rangle + \left\langle u_{n_2\mathbf{k}} \middle| \frac{\partial u_{n_1\mathbf{k}}}{\partial k_x} \right\rangle \left\langle \frac{\partial u_{n_1\mathbf{k}}}{\partial k_y} \middle| u_{n_2\mathbf{k}} \right\rangle \right)\\= &\mathrm{Im} \left( \left\langle \frac{\partial u_{n_1\mathbf{k}}}{\partial k_x} \middle| u_{n_2\mathbf{k}} \right\rangle \left\langle u_{n_2\mathbf{k}} \middle| \frac{\partial u_{n_1\mathbf{k}}}{\partial k_y} \right\rangle + \text{c.c.} \right)\\=& 0\end{aligned}$

所以陈数的表达式可以写为：

$C = -\frac{1}{\pi} \mathrm{Im} \sum_{n=1}^{N_c} \sum_{n' = N_c+1}^{\infty} \int_{\text{BZ}} d\mathbf{k} \, \left\langle \frac{\partial u_{n\mathbf{k}}}{\partial k_x} \middle| u_{n'\mathbf{k}} \right\rangle \left\langle u_{n'\mathbf{k}} \middle| \frac{\partial u_{n\mathbf{k}}}{\partial k_y} \right\rangle$

电子波函数： $\psi_{n\mathbf{k}}(\mathbf{r}) = e^{i \mathbf{k} \cdot \mathbf{r}} u_{n\mathbf{k}}(\mathbf{r})$ ，于是电子波函数的周期部分可以写为 $u_{n\mathbf{k}}(\mathbf{r}) = e^{-i \mathbf{k} \cdot \mathbf{r}} \psi_{n\mathbf{k}}(\mathbf{r})$ ，所以有：

$\langle u_{n'\mathbf{k}}|\nabla_{\mathbf{k}} u_{n\mathbf{k}}\rangle = -i\langle\psi_{n'\mathbf{k}}|\mathbf{r}|\psi_{n\mathbf{k}}\rangle, \quad n \neq n'$

所以陈数可以表达为：

$C = -\frac{1}{\pi}\text{Im}\sum_{n=1}^{N_c}\sum_{n'=N_c+1}^{\infty}\int_{BZ} d\mathbf{k} \langle\Psi_{n\mathbf{k}}|\hat{x}|\Psi_{n'\mathbf{k}}\rangle\langle\Psi_{n'\mathbf{k}}|\hat{y}|\Psi_{n\mathbf{k}}\rangle$

进一步推导（目的是把 $n'\mathbf{k}$ 变成 $n'\mathbf{k'}$ )：

$\begin{aligned} C &= -\frac{1}{\pi}\frac{A_c}{(2\pi)^2}\text{Im}\sum_{n=1}^{N_c}\sum_{n'=N_c+1}^{\infty}\sum_{n''=1}^{\infty}\int_{BZ} d\mathbf{k}\int_{BZ} d\mathbf{k}' \langle\Psi_{n\mathbf{k}}|\hat{x}|\Psi_{n''\mathbf{k'}}\rangle\langle\Psi_{n''\mathbf{k'}}|\Psi_{n'\mathbf{k}}\rangle\langle\Psi_{n'\mathbf{k}}|\hat{y}|\Psi_{n\mathbf{k}}\rangle \\&= -\frac{1}{\pi}\frac{A_c}{(2\pi)^2}\text{Im}\sum_{n=1}^{N_c}\sum_{n'=N_c+1}^{\infty}\sum_{n''=1}^{\infty}\int_{BZ} d\mathbf{k}\int_{BZ} d\mathbf{k}' \langle\Psi_{n\mathbf{k}}|\hat{x}|\Psi_{n''\mathbf{k'}}\rangle \delta_{n''n'}\delta(\mathbf{k}'-\mathbf{k}) \langle\Psi_{n'\mathbf{k}}|\hat{y}|\Psi_{n\mathbf{k}}\rangle \\&= -\frac{1}{\pi}\frac{A_c}{(2\pi)^2}\text{Im}\sum_{n=1}^{N_c}\sum_{n'=N_c+1}^{\infty}\int_{BZ} d\mathbf{k}\int_{BZ} d\mathbf{k}' \langle\Psi_{n\mathbf{k}}|\hat{x}|\Psi_{n'\mathbf{k'}}\rangle\langle\Psi_{n'\mathbf{k'}}|\hat{y}|\Psi_{n\mathbf{k}}\rangle\end{aligned}$

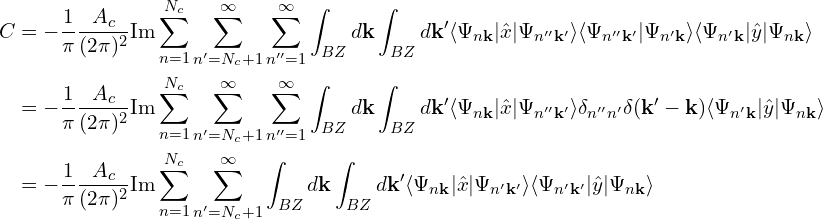
其中，用到单位算符：

$1 = \frac{A_c}{(2\pi)^2} \sum_{n=1}^{\infty} \int_{BZ} d\mathbf{k} |\Psi_{n\mathbf{k}}\rangle \langle\Psi_{n\mathbf{k}}|$

$A_c$ 为元胞的面积。

继续推导（目的是把求和延展到无穷大，这里是 $n''$ ）：

$C = -\frac{1}{\pi} \left(\frac{A_c}{(2\pi)^2}\right)^2 \text{Im} \sum_{n''=1}^{\infty} \sum_{n=1}^{N_c} \sum_{n'=N_c+1}^{\infty} \int_{BZ} d\mathbf{k}'' \int_{BZ} d\mathbf{k} \int_{BZ} d\mathbf{k}' \langle\Psi_{n''\mathbf{k}''} | \Psi_{n\mathbf{k}}\rangle \langle\Psi_{n\mathbf{k}} | \hat{x} | \Psi_{n'\mathbf{k}'}\rangle \langle\Psi_{n'\mathbf{k}'} | \hat{y} | \Psi_{n\mathbf{k}}\rangle$

其中，用到归一化公式：

$\frac{A_c}{(2\pi)^2} \int_{BZ} \mathrm{d}\mathbf{k} \, \delta(\mathbf{k}) = 1$

$\frac{A_c}{(2\pi)^2} \sum_{n''=1}^{\infty} \int_{BZ} \mathrm{d\mathbf{k''}} \langle\Psi_{n''\mathbf{k''}}|\Psi_{n\mathbf{k}}\rangle = 1$

继续推导（符号替换，简化表达式。其中第二个等号用到上面的归一化公式；第三个等号用到迹的循环性质，可证明Pxy项为实数）：

$\begin{aligned} C &= -\frac{1}{\pi} \text{Im} \sum_{n''=1}^{\infty} \int_{BZ} d\mathbf{k}'' \langle\Psi_{n''\mathbf{k}''} | \hat{P}\hat{x}\hat{Q}\hat{y} | \Psi_{n''\mathbf{k}''}\rangle \\ &= -\frac{1}{\pi} \frac{(2\pi)^2}{A_c} \text{Im} \, \text{Tr}_{\text{cell}} \left(\hat{P}\hat{x}\hat{Q}\hat{y}\right) \\ &= \frac{4\pi}{A_c} \text{Im} \, \text{Tr}_{\text{cell}} \left(\hat{P}\hat{x}\hat{P}\hat{y}\right) \\&= \frac{1}{A_c} \text{Tr}_{\text{cell}} \left(\hat{\mathcal{C}}\right)\end{aligned}$