陈数Chern number的计算（定义法，附Python/Matlab代码）

发布时间：2020年1月5日2024年1月25日

最近修改时间：2024年1月25日

其他几篇关于陈数的计算方法：

本篇采用的是定义法计算陈数，而不是用文献[1, 2]中高效的计算方法。定义法在数值计算上可能会比较耗时，但在理解上比较直接和方便：先是计算贝里联络 (Berry connection)，然后再计算贝里曲率 (Berry curvature)，积分得到陈数 (Chern number)。公式为[1]：

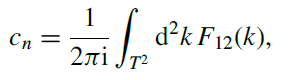
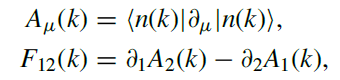
这里以文献[2]中的“量子反常霍尔模型”的哈密顿量为例子，用定义法在数值上计算陈数。

1. Python代码

这里的代码没有考虑波函数连续性，结果可能会出错。考虑波函数规范的代码见本篇第三、四部分。

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/3932
"""

import numpy as np
from math import * 
import time


def hamiltonian(kx, ky):  # 量子反常霍尔QAH模型（该参数对应的陈数为2）
    t1 = 1.0
    t2 = 1.0
    t3 = 0.5
    m = -1.0
    matrix = np.zeros((2, 2), dtype=complex)
    matrix[0, 1] = 2*t1*cos(kx)-1j*2*t1*cos(ky)
    matrix[1, 0] = 2*t1*cos(kx)+1j*2*t1*cos(ky)
    matrix[0, 0] = m+2*t3*sin(kx)+2*t3*sin(ky)+2*t2*cos(kx+ky)
    matrix[1, 1] = -(m+2*t3*sin(kx)+2*t3*sin(ky)+2*t2*cos(kx+ky))
    return matrix


def main():
    start_time = time.time()
    n = 100  # 积分密度
    delta = 1e-9  # 求导的偏离量
    chern_number = 0  # 陈数初始化
    for kx in np.arange(-pi, pi, 2*pi/n):
        for ky in np.arange(-pi, pi, 2*pi/n):
            H = hamiltonian(kx, ky)
            eigenvalue, eigenvector = np.linalg.eig(H)
            vector = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 价带波函数
            # print(np.argsort(np.real(eigenvalue))[0])  # 排序索引（从小到大）
            # print(eigenvalue)  # 排序前的本征值
            # print(np.sort(np.real(eigenvalue)))  # 排序后的本征值（从小到大）
           
            H_delta_kx = hamiltonian(kx+delta, ky) 
            eigenvalue, eigenvector = np.linalg.eig(H_delta_kx)
            vector_delta_kx = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]   # 略偏离kx的波函数

            H_delta_ky = hamiltonian(kx, ky+delta)  
            eigenvalue, eigenvector = np.linalg.eig(H_delta_ky)
            vector_delta_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 略偏离ky的波函数

            H_delta_kx_ky = hamiltonian(kx+delta, ky+delta)  
            eigenvalue, eigenvector = np.linalg.eig(H_delta_kx_ky)
            vector_delta_kx_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 略偏离kx和ky的波函数

            # 价带的波函数的贝里联络(berry connection) # 求导后内积
            A_x = np.dot(vector.transpose().conj(), (vector_delta_kx-vector)/delta)   # 贝里联络Ax（x分量）
            A_y = np.dot(vector.transpose().conj(), (vector_delta_ky-vector)/delta)   # 贝里联络Ay（y分量）
            
            A_x_delta_ky = np.dot(vector_delta_ky.transpose().conj(), (vector_delta_kx_ky-vector_delta_ky)/delta)  # 略偏离ky的贝里联络Ax
            A_y_delta_kx = np.dot(vector_delta_kx.transpose().conj(), (vector_delta_kx_ky-vector_delta_kx)/delta)  # 略偏离kx的贝里联络Ay

            # 贝里曲率(berry curvature)
            F = (A_y_delta_kx-A_y)/delta-(A_x_delta_ky-A_x)/delta

            # 陈数(chern number)
            chern_number = chern_number + F*(2*pi/n)**2
    chern_number = chern_number/(2*pi*1j)
    print('Chern number = ', chern_number)
    end_time = time.time()
    print('运行时间(min)=', (end_time-start_time)/60)


if __name__ == '__main__':
    main()

计算结果：

Chern number = (2.0000002869141356-4.9548136005219324e-09j)

2. Matlab代码

该代码来源于读者提供的代码，经过一些修改。需要说明的是：这里对波函数连续性的问题只是对最简单情况的临时处理，只限于当前的模型和参数。对波函数的正确的处理方式见本篇第三、四部分。

% This code is supported by the website: https://www.guanjihuan.com
% The newest version of this code is on the web page: https://www.guanjihuan.com/archives/3932

% 陈数定义法
clear;clc;
n=100; % 积分密度
delta=1e-9; % 求导的偏离量
C=0; 
for kx=-pi:(1/n):pi
    for ky=-pi:(1/n):pi
        VV=get_vector(HH(kx,ky));
        Vkx=get_vector(HH(kx+delta,ky)); % 略偏离kx的波函数
        Vky=get_vector(HH(kx,ky+delta)); % 略偏离ky的波函数
        Vkxky=get_vector(HH(kx+delta,ky+delta)); % 略偏离kx，ky的波函数
        if  sum((abs(Vkx-VV)))>0.01    % 为了波函数的连续性（这里的不连续只遇到符号问题，所以可以直接这么处理）
            Vkx=-Vkx;
        end
        
        if  sum((abs(Vky-VV)))>0.01
            Vky=-Vky;
        end
        
        if  sum(abs(Vkxky-VV))>0.01
            Vkxky=-Vkxky;
        end
        % 价带的波函数的berry connection，求导后内积
        Ax=VV'*(Vkx-VV)/delta; % Berry connection Ax
        Ay=VV'*(Vky-VV)/delta; % Berry connection Ay
        Ax_delta_ky=Vky'*(Vkxky-Vky)/delta; % 略偏离ky的berry connection Ax
        Ay_delta_kx=Vkx'*(Vkxky-Vkx)/delta; % 略偏离kx的berry connection Ay
        % berry curvature
        F=((Ay_delta_kx-Ay)-(Ax_delta_ky-Ax))/delta;
        % chern number
        C=C+F*(1/n)^2;  
    end
end
C=C/(2*pi*1i)

function vector_new = get_vector(H)
[vector,eigenvalue] = eig(H);
[eigenvalue, index]=sort(diag(eigenvalue), 'descend');
vector_new = vector(:, index(2));
end

function H=HH(kx,ky)
H(1,2)=2*cos(kx)-1i*2*cos(ky);
H(2,1)=2*cos(kx)+1i*2*cos(ky);
H(1,1)=-1+2*0.5*sin(kx)+2*0.5*sin(ky)+2*cos(kx+ky);
H(2,2)=-(-1+2*0.5*sin(kx)+2*0.5*sin(ky)+2*cos(kx+ky));
end

以上matlab代码中，波函数符号会出现波动，因此要增加以下三段代码（原因是波函数整体符号变号，即相位为pi时，仍然是哈密顿量的波函数，但在做波函数相减时会完全不同）：

if  sum((abs(Vkx-VV)))>0.01  
    Vkx=-Vkx;
end
        
if  sum((abs(Vky-VV)))>0.01
    Vky=-Vky;
 end
        
if  sum(abs(Vkxky-VV))>0.01
    Vkxky=-Vkxky;
end

此外，有时加了以上这三段还不够，波函数会时有以下这种形式（一个例子），仍然是不连续：

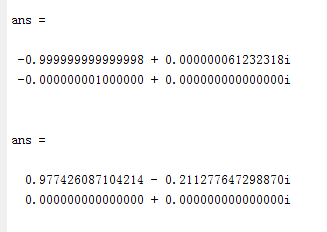
这时候取负号是不能解决波函数的不连续问题，这里临时用取模来处理（原理上是要通过选取规范进行变换，得到波函数（1, 0），下面会提到）：

if abs(VV(1))<0.0001 ||abs(VV(2))<0.0001
      VV=abs(VV);
      Vkx=abs(Vkx);
      Vky=abs(Vky);
      Vkxky=abs(Vkxky);
 end

以上只考虑了2×2的哈密顿量的情况，如果维度再加上去，还会出现其他不连续的情况，在Python中也会遇到这个问题。

3. 总结

这里因为以下波函数都是哈密顿量的解：

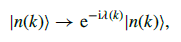
所以规范 (gauge) 的选取在定义法中就显得很重要了，需要选定一个规范，使得局域的波函数连续。以下是文献[1]中截图：

在数值上可以写代码去搜索找个近似的规范（前面提到的“取负号”、“取模”只是两种特殊情况），使得波函数连续，但在计算效率上又降低很多了。搜索连续规范的方法参考：通过二分查找在数值上寻找波函数近似的同一规范（附Python代码）。或者采用固定某个波函数规范的方法，可参考这两篇SSH模型中的Wilson loop（附Python代码）、非简并波函数和简并波函数的固定规范中的代码。这两种方法（二分查找和固定规范）都可以通过开源项目Guan进行函数的调用：https://py.guanjihuan.com。

考虑波函数规范的完整代码见本篇第四部分。

使用定义法的计算效率不是特别高，所以这里还是推荐其他不要求波函数连续性的方法来计算。高效法见参考文献[1, 2]或者参考这篇博文：陈数Chern number的计算（高效法，附Python/Matlab代码）、陈数Chern number的计算（多条能带的高效法，附Python代码）。此外，还有方法：陈数Chern number的计算（Kubo公式，附Python代码）、陈数Chern number的计算（Wilson loop方法，附Python代码）、陈数Chern number的计算（多条能带的Wilson loop方法，附Python代码）等。

4. Python代码（增加寻找连续规范的代码）

前面python代码如果取不同的n，在某些情况下会出现错误的结果。遇到这个问题是正常的，因为前面的波函数没有选取连续的规范。这里增加了寻找连续规范的代码。

（1）使用二分查找的方法

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/3932
"""

import numpy as np
from math import *
import time
import cmath


def hamiltonian(kx, ky):  # 量子反常霍尔QAH模型（该参数对应的陈数为2）
    t1 = 1.0
    t2 = 1.0
    t3 = 0.5
    m = -1.0
    matrix = np.zeros((2, 2), dtype=complex)
    matrix[0, 1] = 2*t1*cos(kx)-1j*2*t1*cos(ky)
    matrix[1, 0] = 2*t1*cos(kx)+1j*2*t1*cos(ky)
    matrix[0, 0] = m+2*t3*sin(kx)+2*t3*sin(ky)+2*t2*cos(kx+ky)
    matrix[1, 1] = -(m+2*t3*sin(kx)+2*t3*sin(ky)+2*t2*cos(kx+ky))
    return matrix


def main():
    start_time = time.time()
    n = 20  # 积分密度
    delta = 1e-9  # 求导的偏离量
    chern_number = 0  # 陈数初始化
    for kx in np.arange(-pi, pi, 2*pi/n):
        for ky in np.arange(-pi, pi, 2*pi/n):
            H = hamiltonian(kx, ky)
            eigenvalue, eigenvector = np.linalg.eig(H)
            vector = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 价带波函数
           
            H_delta_kx = hamiltonian(kx+delta, ky) 
            eigenvalue, eigenvector = np.linalg.eig(H_delta_kx)
            vector_delta_kx = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]   # 略偏离kx的波函数

            H_delta_ky = hamiltonian(kx, ky+delta)  
            eigenvalue, eigenvector = np.linalg.eig(H_delta_ky)
            vector_delta_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 略偏离ky的波函数

            H_delta_kx_ky = hamiltonian(kx+delta, ky+delta)  
            eigenvalue, eigenvector = np.linalg.eig(H_delta_kx_ky)
            vector_delta_kx_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 略偏离kx和ky的波函数

            vector_delta_kx = find_vector_with_the_same_gauge(vector_delta_kx, vector)
            vector_delta_ky = find_vector_with_the_same_gauge(vector_delta_ky, vector)
            vector_delta_kx_ky  = find_vector_with_the_same_gauge(vector_delta_kx_ky, vector)

            # 价带的波函数的贝里联络(berry connection) # 求导后内积
            A_x = np.dot(vector.transpose().conj(), (vector_delta_kx-vector)/delta)   # 贝里联络Ax（x分量）
            A_y = np.dot(vector.transpose().conj(), (vector_delta_ky-vector)/delta)   # 贝里联络Ay（y分量）
            
            A_x_delta_ky = np.dot(vector_delta_ky.transpose().conj(), (vector_delta_kx_ky-vector_delta_ky)/delta)  # 略偏离ky的贝里联络Ax
            A_y_delta_kx = np.dot(vector_delta_kx.transpose().conj(), (vector_delta_kx_ky-vector_delta_kx)/delta)  # 略偏离kx的贝里联络Ay

            # 贝里曲率(berry curvature)
            F = (A_y_delta_kx-A_y)/delta-(A_x_delta_ky-A_x)/delta

            # 陈数(chern number)
            chern_number = chern_number + F*(2*pi/n)**2
    chern_number = chern_number/(2*pi*1j)
    print('Chern number = ', chern_number)
    end_time = time.time()
    print('运行时间(min)=', (end_time-start_time)/60)


def find_vector_with_the_same_gauge(vector_1, vector_0):
    # 寻找近似的同一的规范
    phase_1_pre = 0
    phase_2_pre = pi
    n_test = 10001
    for i0 in range(n_test):
        test_1 = np.sum(np.abs(vector_1*cmath.exp(1j*phase_1_pre) - vector_0))
        test_2 = np.sum(np.abs(vector_1*cmath.exp(1j*phase_2_pre) - vector_0))
        if test_1 < 1e-8:
            phase = phase_1_pre
            # print('Done with i0=', i0)
            break
        if i0 == n_test-1:
            phase = phase_1_pre
            print('Gauge Not Found with i0=', i0)
        if test_1 < test_2:
            if i0 == 0:
                phase_1 = phase_1_pre-(phase_2_pre-phase_1_pre)/2
                phase_2 = phase_1_pre+(phase_2_pre-phase_1_pre)/2
            else:
                phase_1 = phase_1_pre
                phase_2 = phase_1_pre+(phase_2_pre-phase_1_pre)/2
        else:
            if i0 == 0:
                phase_1 = phase_2_pre-(phase_2_pre-phase_1_pre)/2
                phase_2 = phase_2_pre+(phase_2_pre-phase_1_pre)/2
            else:
                phase_1 = phase_2_pre-(phase_2_pre-phase_1_pre)/2
                phase_2 = phase_2_pre 
        phase_1_pre = phase_1
        phase_2_pre = phase_2
    vector_1 = vector_1*cmath.exp(1j*phase)
    # print('二分查找找到的规范=', phase)   
    return vector_1


if __name__ == '__main__':
    main()

（2）使用固定规范的方法

补充说明：固定规范除了循环查找的方法外，还可以通过乘一个相反的相位角来实现，效率更高。参考这篇：非简并波函数和简并波函数的固定规范。

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/3932
"""

import numpy as np
from math import *
import time
import cmath


def hamiltonian(kx, ky):  # 量子反常霍尔QAH模型（该参数对应的陈数为2）
    t1 = 1.0
    t2 = 1.0
    t3 = 0.5
    m = -1.0
    matrix = np.zeros((2, 2), dtype=complex)
    matrix[0, 1] = 2*t1*cos(kx)-1j*2*t1*cos(ky)
    matrix[1, 0] = 2*t1*cos(kx)+1j*2*t1*cos(ky)
    matrix[0, 0] = m+2*t3*sin(kx)+2*t3*sin(ky)+2*t2*cos(kx+ky)
    matrix[1, 1] = -(m+2*t3*sin(kx)+2*t3*sin(ky)+2*t2*cos(kx+ky))
    return matrix


def main():
    start_time = time.time()
    n = 20  # 积分密度
    delta = 1e-9  # 求导的偏离量
    chern_number = 0  # 陈数初始化
    for kx in np.arange(-pi, pi, 2*pi/n):
        for ky in np.arange(-pi, pi, 2*pi/n):
            H = hamiltonian(kx, ky)
            eigenvalue, eigenvector = np.linalg.eig(H)
            vector = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 价带波函数
           
            H_delta_kx = hamiltonian(kx+delta, ky) 
            eigenvalue, eigenvector = np.linalg.eig(H_delta_kx)
            vector_delta_kx = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]   # 略偏离kx的波函数

            H_delta_ky = hamiltonian(kx, ky+delta)  
            eigenvalue, eigenvector = np.linalg.eig(H_delta_ky)
            vector_delta_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 略偏离ky的波函数

            H_delta_kx_ky = hamiltonian(kx+delta, ky+delta)  
            eigenvalue, eigenvector = np.linalg.eig(H_delta_kx_ky)
            vector_delta_kx_ky = eigenvector[:, np.argsort(np.real(eigenvalue))[0]]  # 略偏离kx和ky的波函数

            index = np.argmax(np.abs(vector))
            precision = 0.0001
            vector = find_vector_with_fixed_gauge_by_making_one_component_real(vector, precision=precision, index=index)
            vector_delta_kx = find_vector_with_fixed_gauge_by_making_one_component_real(vector_delta_kx, precision=precision, index=index)
            vector_delta_ky = find_vector_with_fixed_gauge_by_making_one_component_real(vector_delta_ky, precision=precision, index=index)
            vector_delta_kx_ky  = find_vector_with_fixed_gauge_by_making_one_component_real(vector_delta_kx_ky, precision=precision, index=index)

            # 价带的波函数的贝里联络(berry connection) # 求导后内积
            A_x = np.dot(vector.transpose().conj(), (vector_delta_kx-vector)/delta)   # 贝里联络Ax（x分量）
            A_y = np.dot(vector.transpose().conj(), (vector_delta_ky-vector)/delta)   # 贝里联络Ay（y分量）
            
            A_x_delta_ky = np.dot(vector_delta_ky.transpose().conj(), (vector_delta_kx_ky-vector_delta_ky)/delta)  # 略偏离ky的贝里联络Ax
            A_y_delta_kx = np.dot(vector_delta_kx.transpose().conj(), (vector_delta_kx_ky-vector_delta_kx)/delta)  # 略偏离kx的贝里联络Ay

            # 贝里曲率(berry curvature)
            F = (A_y_delta_kx-A_y)/delta-(A_x_delta_ky-A_x)/delta

            # 陈数(chern number)
            chern_number = chern_number + F*(2*pi/n)**2
    chern_number = chern_number/(2*pi*1j)
    print('Chern number = ', chern_number)
    end_time = time.time()
    print('运行时间(min)=', (end_time-start_time)/60)


def find_vector_with_fixed_gauge_by_making_one_component_real(vector, precision=0.005, index=None):
    vector = np.array(vector)
    if index == None:
        index = np.argmax(np.abs(vector))
    sign_pre = np.sign(np.imag(vector[index]))
    for phase in np.arange(0, 2*np.pi, precision):
        sign =  np.sign(np.imag(vector[index]*cmath.exp(1j*phase)))
        if np.abs(np.imag(vector[index]*cmath.exp(1j*phase))) < 1e-9 or sign == -sign_pre:
            break
        sign_pre = sign
    vector = vector*cmath.exp(1j*phase)
    if np.real(vector[index]) < 0:
        vector = -vector
    return vector 


if __name__ == '__main__':
    main()

参考资料：

[1] Chern Numbers in Discretized Brillouin Zone: Efficient Method of Computing (Spin) Hall Conductances

[2] Route towards Localization for Quantum Anomalous Hall Systems with Chern Number 2

[3] Berry phase effects on electronic properties

[4] Quantum anomalous Hall effect in graphene from Rashba and exchange effects

[5] Localization trajectory and Chern-Simons axion coupling for bilayer quantum anomalous Hall systems

23,547 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】

Published by guanjihuan

View all posts by guanjihuan

58 thoughts on “陈数Chern number的计算（定义法，附Python/Matlab代码）”

搬砖人说道：

2024年8月6日 15:49

你好，波函数不连续是什么意思呀，跟两条能带有交点是一个意思吗，如果是孤立的能带，那波函数连续吗

回复
1. guanjihuan说道：
  
  2024年8月6日 16:27
  
  这里说的“连续”是指布里渊区离散后相邻 k 点之间波函数的连续性，例如 phi(k) 和 phi(k+delta) 波函数应该取相同的规范，从而解决求导的发散问题。
  
  回复
  1. 搬砖人说道：
    
    2024年8月6日 16:53
    
    谢谢，除了定义法需要考虑波函数连续性，其他几种方法用考虑吗？还有就是你提到的这几种计算陈数的方法分别都在什么模型或材料中用啊？感谢
    
    回复
    1. guanjihuan说道：
      
      2024年8月6日 17:01
      
      （1）其他几种方法都不需要考虑波函数的连续性，主要是看公式中是否需要对波函数求导。
      （2）这些计算方法都是可以用的，多能带的方法会更通用些，适用于能带简并或者能带交叉的情况。
      （3）公式都是拓扑不变量的定义，没有指定的模型或材料。一般要求有波函数信息和布里渊区范围，因为需要对布里渊区积分才可以得到陈数。
      （4）如果是具体材料的拓扑不变量的计算，可以用一些软件直接算，例如wanniertool等。
      
      回复
      1. 匿名说道：
        
        2024年8月6日 19:23
        
        谢谢，那怎么判断波函数什么时候连续，什么时候不连续（需要考虑规范）呢
        
        回复
        
        guanjihuan说道：
        
        2024年8月7日 09:43
        
        数值计算上一般波函数不会连续，因为波函数的规范具有任意性。如果公式中需要求导等操作，那么需要考虑固定一个规范。
        
        回复
dddlll说道：

2024年6月27日 21:17

博主你好，我发现我matlab给的两分量波函数的其中一个分量已经是纯实的了，这是否认为它已经完成了固定规范的操作，可以直接用于差分呢？

回复
1. guanjihuan说道：
  
  2024年6月28日 14:28
  
  需要每个k点（或者相邻k点的）的波函数的某个分量都是纯实的，这样就可以。而且该分量不能为零，不然没法判断是否完成统一的规范。
  
  回复
匿名说道：

2024年5月30日 19:49

关老师您好，请问zak相位是不是只能针对unit cell 的一条能带去计算，因为我看zak相的计算涉及到对布里渊区的积分。如果我的系统是有缺陷的，只有左右是周期性的，上下边界则用的是散射边条或者完美电导体边界条件，那这种情况还能计算单元结构能带的zak相吗？

回复
1. guanjihuan说道：
  
  2024年5月30日 20:18
  
  不变量的计算比较多的是在倒空间中进行计算。有缺陷时，如果有元胞，那么可以扩大元胞进行计算；如果没有元胞，那么就没法计算，或者只能从实空间的角度去计算，定义会麻烦很多。
  
  回复
匿名说道：

2024年2月28日 21:52

关老师您好，请问这个"定义法+您的二分法固定波函数规范"可以用来计算多条能带交叉简并的情况吗？我的一个设想是，对于交叉简并的k点，计算此点的贝里曲率会有问题，则我们可以不算这个点，即设一个阈值，舍去近似交叉简并的点的贝里曲率在积分中对陈数的贡献，然后对贝里曲率计算积分，得到的陈数应该和多条能带的wilson loop法得到的结果可能会差不多？因为网格可以取密一些。

回复
1. guanjihuan说道：
  
  2024年2月29日 21:01
  
  嗯，可能是可以的，可能需要考虑的有：（1）需要对数值做一个判断，另外要把积分长度也要考虑进去，因为可能会有变化。（2）这种方法只支持交叉的能带，不支持完全重合的能带。（3）还有网格是否可以取密一些，这个还不好说，因为取到一定精度时，会近似于简并了，这需要具体数值测试下。
  
  回复
  1. 匿名说道：
    
    2024年3月1日 09:07
    
    嗯嗯，谢谢关老师~
    
    回复
tang说道：

2023年11月27日 17:33

关老师，您好，我在复现一篇正方晶格的二维结构的拓扑结构（10.1103/PhysRevLett.126.113902），Comsol可以得到和文章中一致，但是我想算一下她的贝利曲率不知道看您的哪一篇文章符合计算的模型？

回复
1. guanjihuan说道：
  
  2023年11月27日 21:27
  
  如果是紧束缚模型，几种方法都是可以的。我个人推荐：陈数Chern number的计算（高效法，附Python/Matlab代码）。如果能带有交叉或者简并的情况，参考这篇：陈数Chern number的计算（多条能带的高效法，附Python代码）.。
  
  回复
匿名说道：

2023年9月25日 17:06

关老师，如果哈密顿量是4×4的矩阵，matlab程序该怎么处理呢（呜呜呜，希望您能指点一下我）

回复
1. guanjihuan说道：
  
  2023年9月25日 17:17
  
  计算过程是一样的，你可以将python代码转义成matlab。如果不熟悉python，可以用人工智能作为辅助进行转义。
  
  我个人是推荐这个方法：陈数Chern number的计算（高效法，附Python/Matlab代码）。如果两个价带有交叉或者简并的情况，推荐这个方法：陈数Chern number的计算（多条能带的高效法，附Python代码）。
  
  回复
  1. 匿名说道：
    
    2023年10月12日 09:02
    
    也就是说定义法是无关哈密顿量的维度，以及无关是否是非厄米与厄米吗？
    
    回复
    1. guanjihuan说道：
      
      2023年10月12日 09:27
      
      只是对于二维的情况。非厄米有非厄米的拓扑定义。
      
      回复
郭鹏宇说道：

2023年6月25日 13:36

关老师，因为我刚接触拓扑，有些东西不是特别懂，我想请教一下有没有什么文章或者教材讲解陈数之类的拓扑不变量的计算过程和计算思路，因为您的代码里面有些步骤我不太理解为什么要这样做，比如为什么要用到“略偏离ky的berry connection Ax”。

回复
1. guanjihuan说道：
  
  2023年6月25日 23:28
  
  这里就是求导的意思。可参考综述文献：Berry phase effects on electronic properties。
  
  回复
冬冬说道：

2021年12月4日 15:26

请问最后积分时为什么是乘以(1/n)^2而不是delta^2呢？是不是这样才能覆盖整个积分区域，那理想情况是不是将(1/n)和delta取相同的值

回复
1. guanjihuan说道：
  
  2021年12月5日 06:30
  
  一个是积分的步长，一个是求导的步长。因为积分步长和循环次数有关，所以不能取太小，不然计算时间会很长。求导步长是越小越好，积分步长也是越小越好。两者可以取为相同的值，也可以取为不同的值，都只是对极限（极小）的近似。
  
  回复
匿名说道：

2021年11月17日 00:10

博主，你好，我想请教一个问题，在一般的拓扑体系中，体系哈密顿量满足时间反演对称，那该体系对应的陈数必为零。那如果一个非平庸的拓扑体系哈密顿量，不满足时间反演对称，该体系的陈数有没有可能也是为零的？

回复
1. guanjihuan说道：
  
  2021年11月17日 12:01
  
  不满足时间反演对称不一定是拓扑的。你指的非平庸的拓扑体系看指的是什么。如果是陈拓扑绝缘体，那么陈数就不为零。如果是Z2拓扑绝缘体，那么陈数为零，但这个是满足时间反演对称性的。如果是其他的拓扑体系，比如拓扑半金属、高阶拓扑绝缘体等，是由其他的不变量来描述。
  
  回复
匿名说道：

2021年10月26日 16:04

请问一下我带入一个方格子哈密顿量算出来是陈数-1咋办，这是啥样的拓扑性质呢

回复
1. guanjihuan说道：
  
  2021年10月26日 18:51
  
  正负1都是拓扑的，非平庸的。有需要可以取绝对值。
  
  回复
hua说道：

2021年5月9日 19:41

您好，我有个问题想问一下：在SSH model中，我们先用周期性边界条件得到绕数，再用开边界得到边缘态，那么在二维的时候，是不是在两个方向上都得采用周期性边界条件，得到陈数，然后再对一个方向用开边界条件，得到边缘态？

回复
1. guanjihuan说道：
  
  2021年5月20日 17:04
  
  不是周期性边界条件，而是本身考虑的就是二维的体系，包含了kx和ky，然后计算陈数。在开放边界条件下，会存在边缘态。
  
  回复
  1. 匿名说道：
    
    2021年5月25日 14:16
    
    懂了，谢谢
    
    回复
匿名说道：

2021年3月29日 21:06

这个是只要是二阶矩阵哈密顿量就可以吗，我代入了一个正方格子模型，发现随着积分密度的变化，chern数有很大的变化

回复
1. guanjihuan说道：
  
  2021年3月30日 19:41
  
  正方格子的chern数为零，值应该应该是在1e-8以下，数值变化很正常，理论上都是0。
  
  回复
  1. 匿名说道：
    
    2021年12月2日 19:42
    
    请问我取了积分步长也是1e-9，计算时间很久很久，这是正常的吗
    
    回复
    1. guanjihuan说道：
      
      2021年12月3日 02:13
      
      正常呀，但不需要精度算那么高。你这相当于循环了2*pi*10^9次了。
      
      回复
匿名说道：

2021年3月28日 15:03

这个是不是只要是二阶哈密顿量，带入H（1，1）H(1,2)H(2,1)H(2,2)就可以计算出chern数，我看到我带去运行的命令窗口H一直在闪

回复
1. guanjihuan说道：
  
  2021年3月28日 19:14
  
  是少加了分号，赋值一直在输出显示？
  
  回复
  1. 匿名说道：
    
    2021年3月29日 13:06
    
    已经解决了，确实少加了分号，谢谢
    
    回复
匿名说道：

2021年3月27日 17:04

感谢博主的分享，我在重复博主分享的参考文献[1]的时候出现了一个问题，使用文献[1]中的(5)式计算的时候发现会出现非常大的值，而且求和为0，博主能帮我解决一下下吗？

回复
1. guanjihuan说道：
  
  2021年3月27日 19:05
  
  是因为波函数不连续吗？
  
  回复
张泽说道：

2020年10月29日 13:49

同学你好，有个算陈数的课题想请教一下你，方便加个微信嘛

回复
1. guanjihuan说道：
  
  2020年10月29日 14:04
  
  嗯，可以的
  
  回复
2. guanjihuan说道：
  
  2020年10月29日 14:10
  
  我微信号或者微信二维码在https://www.guanjihuan.com/about
  
  回复
匿名说道：

2020年10月13日 16:56

请问一下，在python的方法中，main函数的作用是什么，能否把它改成其他函数。比如在最后用return语句

回复
1. guanjihuan说道：
  
  2020年10月13日 19:45
  def main()是主函数，其实也是普通的函数，可以用别的符号代替，例如def zhuhanshu()。因为在程序中，我直接运行main()，所以它就执行该函数的内容，该语句经常也写为
  
  if __name__ == '__main__': # 如果是当前文件直接运行，执行main()函数中的内容；如果是import当前文件，则不执行。 main()
  回复
清欣说道：

2020年8月22日 12:13

你好，请问为何要设置偏离kx和ky的Ax,Ay呢？从公式上看delta的取值对于计算结果的大小有非常大的影响，在最后F的公式中就需要除以delta的平方，请问是什么原因？

回复
1. guanjihuan说道：
  
  2020年8月22日 12:40
  
  没有平方。delta取小量就可以，影响不大。整个过程就是数值上的求导，把求导变成除法。
  
  回复
李会昌说道：

2020年7月3日 16:20

太感谢了！支持支持
求得的陈数是一个近似的整数，请问有没有计算方法能得到一个确定的整数呢？

回复
1. guanjihuan说道：
  
  2020年7月3日 16:37
  
  把积分的步长取小一点，就会接近于一个整数。步长越小，越接近，但计算的时间会增加很多，你可以计算试一下。所以取一个合理的步长就可以了，数值上的计算有一些误差也是正常的，误差很小时就可以忽略不计。
  
  回复
flyzenr说道：

2020年5月25日 18:00

同学，你好！想问你两个问题。
1. 为什么 matlab 里面中 C=C+F*(1/n)^2; 而python中 chern_number = chern_number + F*(2*pi/n)**2。为什么这里matlab中计算公式少了 2*pi 呢?
2. 对于不含参的哈密顿量，你知道有什么方法可以计算chern number吗？

回复
1. guanjihuan说道：
  
  2020年5月25日 19:54
  
  （1）两个代码的积分密度n表示的意思有点不一样。Python代码中步长是2*pi/n，Matlab中步长是1/n。也可以试着把代码改成一样的。
  （2）Chern number的计算一般都是在倒空间吧。如果是实空间的，要傅里叶变换到倒空间，然后就存在参数kx和ky。
  
  回复
匿名说道：

2020年5月25日 10:11

请问一下，陈数的本征态对应的本征值是哪个呀？

回复
1. guanjihuan说道：
  
  2020年5月25日 10:22
  
  [vector,eigenvalue] = eig(H);
  这个语句。哈密顿量的本质态为vector和本质值为eigenvalue，eig(H)计算出来的结果是一一对应的。
  
  回复
  1. 匿名说道：
    
    2020年5月25日 10:46
    
    谢谢呢。
    
    回复
匿名说道：

2020年5月23日 20:27

非常感谢博主的分享，请问一下，如果是含三个参数，例如在三维空间的陈数能不能改成取特定值，在博主的程序的基础上加个循环取某些特定的值呢？

回复
1. guanjihuan说道：
  
  2020年5月23日 21:36
  
  我没了解过，不知道三维的陈数是否存在？这个比较偏数学。你可以找一些文献看看，如果某维度可行的话，积分的话肯定是要在对应的维度积分。我目前只接触到二维的，即使是三维的Weyl半金属，也是固定一个参数，按切片来计算陈数的。（其他读者有了解的可以留言）
  
  回复
flyzenr说道：

2020年5月19日 12:01

哈喽，同学你好，我想问一个问题，code里面的陈数的计算
# 陈数(chern number)
chern_number = chern_number + F*(2*pi/n)**2，
中的 F*(2*pi/n)**2是怎么来的呀？

回复
1. guanjihuan说道：
  
  2020年5月19日 12:35
  
  要对贝里曲率F积分。布里渊区正方形两个边长分别分成(2*pi/n)份，所以面积分成了(2*pi/n)**2份。
  
  回复
  1. 匿名说道：
    
    2020年5月19日 14:36
    
    嗷嗷，明白了谢谢同学解答
    
    回复