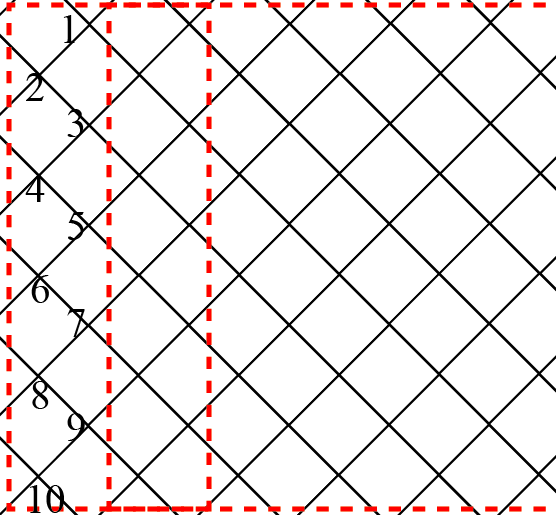
这里画出最简单的体系“方格子”在准一维情况下的能带图。下面是方格子的示意图(宽度为10,红虚线圈出了两个元胞):
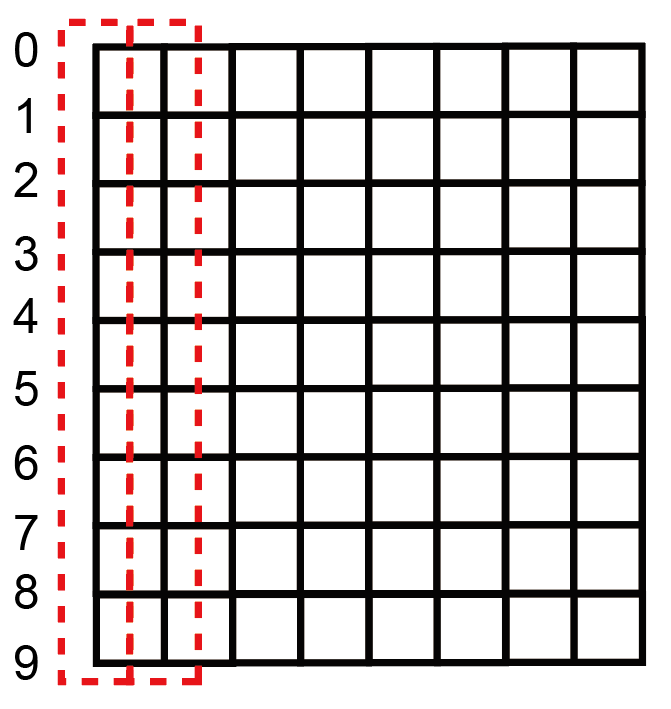
以宽度为3为例(图中画出的是宽度为10),写出实空间的哈密顿量:
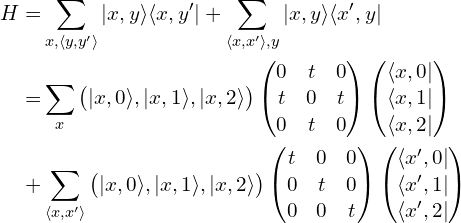
第一项是元胞内的跃迁项。第二项是元胞间的跃迁项,对所有最近邻的求和。
离散格子的傅里叶变换可以参考博文:离散格子的傅里叶变换和反傅里叶变换
这里只在一个方向做傅里叶变换。傅里叶变换后得到倒空间的哈密顿量为:
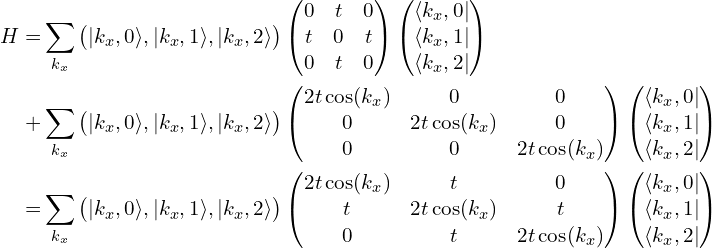
代码如下:
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/3895
"""
import numpy as np
import matplotlib.pyplot as plt
from math import *
import cmath
import functools
def hamiltonian(k, N, t): # 准一维方格子哈密顿量
# 初始化为零矩阵
h00 = np.zeros((N, N), dtype=complex)
h01 = np.zeros((N, N), dtype=complex)
for i in range(N-1): # 原胞内的跃迁h00
h00[i, i+1] = t
h00[i+1, i] = t
for i in range(N): # 原胞间的跃迁h01
h01[i, i] = t
matrix = h00 + h01*cmath.exp(1j*k) + h01.transpose().conj()*cmath.exp(-1j*k)
return matrix
def main():
H_k = functools.partial(hamiltonian, N=10, t=1)
k = np.linspace(-pi, pi, 300)
plot_bands_one_dimension(k, H_k)
def plot_bands_one_dimension(k, hamiltonian):
dim = hamiltonian(0).shape[0]
dim_k = k.shape[0]
eigenvalue_k = np.zeros((dim_k, dim))
i0 = 0
for k0 in k:
matrix0 = hamiltonian(k0)
eigenvalue, eigenvector = np.linalg.eig(matrix0)
eigenvalue_k[i0, :] = np.sort(np.real(eigenvalue[:]))
i0 += 1
for dim0 in range(dim):
plt.plot(k, eigenvalue_k[:, dim0], '-k')
plt.show()
if __name__ == '__main__':
main()
能带为:
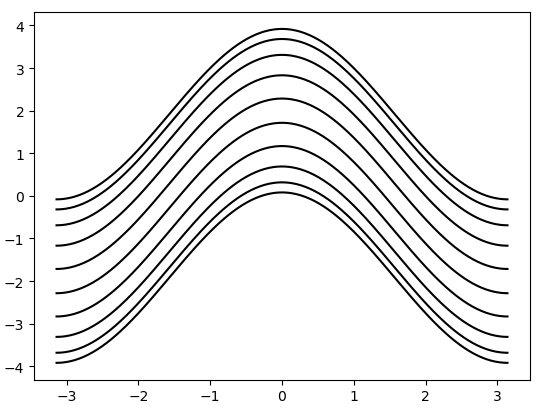
此外,如果是沿着斜对角方向的准一维条带,只要写出内部跃迁矩阵和元胞之间的跃迁矩阵后,傅里叶变换仍然类似于一维链的情况。如下图所示:
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】
关老师,全空间的能带图怎么画啊
对倒空间的哈密顿量的每个(kx,ky)求本征值或者赋值就好了。如果只有实空间的哈密顿量,那么需要在两个方向上进行傅里叶变换。对于方格子,差不多是 2cos(kx)+2cos(ky) 的形式。
谢谢
关老师,我想问一下,QWZ模型的准一维能带图应该怎么处理?
s00=sin(k)*sy+(cos(k)+u)*sz;
h00=t*diag(ones(1,N-1),1)+t*diag(ones(1,N-1),-1);
H00=kron(h00,s00);
s01=(sz+1i*sx)/2;
h01=t*diag(ones(1,N));
H01=kron(h01,s01);
H=H00+H01*exp(1j*k)+H01'*exp(-1j*k(i));
这里是我写的准一维处理,但是得到结果不对。
模型的介绍可以参考这本书 2016 - Asbóth et al. - A Short Course on Topological Insulators, 里面提到:This model is also important because it forms the basic building block of the Bernevig-Hughes-Zhang model for the Quantum Spin Hall Effect, and thus it is also sometimes called “half BHZ”.
具体的代码书写可以参考:
离散格子的傅里叶变换和反傅里叶变换、
BHZ模型的自旋陈数和Z2不变量(附Python、Matlab代码)、
BHZ模型哈密顿量与准一维体系的能带图(附Python代码)。
这个的宽度是9吧,应该不是10,相应的后面的宽度是2
嗯,都是可以的,看怎么定义了。这里说的宽度指的是元胞中有几个原子。
关老师,我想问一个问题,不管是在方格子还是在六边形中,在使用哈密顿量求解边界态的时候,经常会有这样一个循环,我一直不太理解这是什么意思,可以请教一下吗?(MATLAB代码)
num=101
k=linspace(0,2,num);
for i=1:num
H=H00+H01*exp(1j*k(i)*pi)+H01'*exp(-1j*k(i)*pi);
eigenvalue=eig(H);
E(:,i)=eigenvalue;
end
代码为对不同的k,求哈密顿量H本征值。这里是条带(ribbon)的哈密顿量,和一维链的傅里叶变换形式差不多,参考:离散格子的傅里叶变换和反傅里叶变换。
您好!请问代码最后对特征能量数组进行储存的时候,为什么要加一个排序操作(np.sort)呢?
np.linalg.eig的特征值是没有排序的。参考:np.linalg.eig和np.linalg.eigh的区别。
博主,您好!对于这个模型,哈密顿量矩阵对角线上的量来自于胞间的跃迁,比如x1到x‘1为t,这个根据图是可以理解的。不过在您的另一篇博文中,有用到广州大学张艳阳老师课件的那一页,在给出石墨烯哈密顿量的时候,哈密顿量矩阵的主对角线上的元都为零。石墨烯不是也有胞间跃迁的嘛,为什么矩阵对角元上元素都为0呢?
对于胞间跃迁,如果是编号i的位置到编号i的位置有跃迁,那么在主对角线上写。如果是编号i的位置到编号j (j≠i) 的位置有跃迁,那么不在主对角线上写,主对角线上可以为0。
好的,谢谢关老师!请问这个模型有没有详细的书可以参阅呢?目前学得一知半解,也不能够自己独立推导出一个模型的哈密顿量。
就是用这个方法写哈密顿量矩阵,不局限于石墨烯模型、方格子,请问哪本书有介绍呢
我好像没有看到,你可以自己找一找。紧束缚模型直接写就是这个原理,对于具体材料的紧束缚模型需要从第一性原理计算给出。
好的谢谢您~
在元胞内采取周期性边界条件,对应矩阵的第一行末尾和最后一行起始元素都为t(而不是0)是否更加合理,那样的话由于更好的对称性系统能量将会产生简并。
嗯,都可以的,看考虑的是什么问题。如果需要研究体态、忽略边缘态,可以这么考虑。
楼主您好,请问假如原胞内的跃迁不是一个数而是一个矩阵,那么构建哈密顿量的时候怎么赋值呢?
可参考:BHZ模型哈密顿量与准一维体系的能带图(附Python代码)。
问一下博主,这个方格子示意图水平方向是无限长的是吗?
是的
大神,想请教一个问题,对于两个方向都是有限的模型,比如你那篇方格子的哈密顿量,哈密顿量里面都是固定的跃迁系数,与k无关,如何画出他们的能带结构呢?
能带是要求在某个方向是周期性的,这样才可以傅里叶变换,才有动量k。如果体系没有周期性,当然也可以把整个有限宽度和高度的体系当成元胞,在某个方向上周期性重复,这样也能画出能带,也能体现出该体系的性质。但这种情况能带的结构会比较乱,这是因为元胞内包含的自由度比较高,对应的带也就比较多了。