一、使用格林函数算法进行计算
局域电流 (Local current) 公式见参考资料[1,2]。
代码如下（以方格子为例，在中间区域加了一个势垒）。
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/3888
"""
import numpy as np
import matplotlib.pyplot as plt
import time
def matrix_00(width=10): # 电极元胞内跃迁，width不赋值时默认为10
h00 = np.zeros((width, width))
for width0 in range(width-1):
h00[width0, width0+1] = 1
h00[width0+1, width0] = 1
return h00
def matrix_01(width=10): # 电极元胞间跃迁，width不赋值时默认为10
h01 = np.identity(width)
return h01
def matrix_LC(width=10, length=300): # 左电极跳到中心区
h_LC = np.zeros((width, width*length))
for width0 in range(width):
h_LC[width0, width0] = 1
return h_LC
def matrix_CR(width=10, length=300): # 中心区跳到右电极
h_CR = np.zeros((width*length, width))
for width0 in range(width):
h_CR[width*(length-1)+width0, width0] = 1
return h_CR
def matrix_center(width=10, length=300): # 中心区哈密顿量
hamiltonian = np.zeros((width*length, width*length))
for length0 in range(length-1):
for width0 in range(width):
hamiltonian[width*length0+width0, width*(length0+1)+width0] = 1 # 长度方向跃迁
hamiltonian[width*(length0+1)+width0, width*length0+width0] = 1
for length0 in range(length):
for width0 in range(width-1):
hamiltonian[width*length0+width0, width*length0+width0+1] = 1 # 宽度方向跃迁
hamiltonian[width*length0+width0+1, width*length0+width0] = 1
# 中间加势垒
for j0 in range(6):
for i0 in range(6):
hamiltonian[width*(int(length/2)-3+j0)+int(width/2)-3+i0, width*(int(length/2)-3+j0)+int(width/2)-3+i0]= 1e8
return hamiltonian
def main():
start_time = time.time()
fermi_energy = 0
width = 60
length = 100
h00 = matrix_00(width)
h01 = matrix_01(width)
G_n = Green_n(fermi_energy+1j*1e-9, h00, h01, width, length)
# 下面是提取数据并画图
direction_x = np.zeros((width, length))
direction_y = np.zeros((width, length))
for length0 in range(length-1):
for width0 in range(width):
direction_x[width0, length0] = G_n[width*length0+width0, width*(length0+1)+width0]
for length0 in range(length):
for width0 in range(width-1):
direction_y[width0, length0] = G_n[width*length0+width0, width*length0+width0+1]
# print(direction_x)
# print(direction_y)
X, Y = np.meshgrid(range(length), range(width))
plt.quiver(X, Y, direction_x, direction_y)
plt.show()
end_time = time.time()
print('运行时间=', end_time-start_time)
def transfer_matrix(fermi_energy, h00, h01, dim): # 转移矩阵T。dim是传递矩阵h00和h01的维度
transfer = np.zeros((2*dim, 2*dim), dtype=complex)
transfer[0:dim, 0:dim] = np.dot(np.linalg.inv(h01), fermi_energy*np.identity(dim)-h00) # np.dot()等效于np.matmul()
transfer[0:dim, dim:2*dim] = np.dot(-1*np.linalg.inv(h01), h01.transpose().conj())
transfer[dim:2*dim, 0:dim] = np.identity(dim)
transfer[dim:2*dim, dim:2*dim] = 0 # a:b代表 a <= x < b
return transfer # 返回转移矩阵
def green_function_lead(fermi_energy, h00, h01, dim): # 电极的表面格林函数
transfer = transfer_matrix(fermi_energy, h00, h01, dim)
eigenvalue, eigenvector = np.linalg.eig(transfer)
ind = np.argsort(np.abs(eigenvalue))
temp = np.zeros((2*dim, 2*dim))*(1+0j)
i0 = 0
for ind0 in ind:
temp[:, i0] = eigenvector[:, ind0]
i0 += 1
s1 = temp[dim:2*dim, 0:dim]
s2 = temp[0:dim, 0:dim]
s3 = temp[dim:2*dim, dim:2*dim]
s4 = temp[0:dim, dim:2*dim]
right_lead_surface = np.linalg.inv(fermi_energy*np.identity(dim)-h00-np.dot(np.dot(h01, s2), np.linalg.inv(s1)))
left_lead_surface = np.linalg.inv(fermi_energy*np.identity(dim)-h00-np.dot(np.dot(h01.transpose().conj(), s3), np.linalg.inv(s4)))
return right_lead_surface, left_lead_surface # 返回右电极的表面格林函数和左电极的表面格林函数
def self_energy_lead(fermi_energy, h00, h01, width, length): # 电极的自能
h_LC = matrix_LC(width, length)
h_CR = matrix_CR(width, length)
right_lead_surface, left_lead_surface = green_function_lead(fermi_energy, h00, h01, width)
right_self_energy = np.dot(np.dot(h_CR, right_lead_surface), h_CR.transpose().conj())
left_self_energy = np.dot(np.dot(h_LC.transpose().conj(), left_lead_surface), h_LC)
return right_self_energy, left_self_energy # 返回右电极的自能和左电极的自能
def Green_n(fermi_energy, h00, h01, width, length): # 计算G_n
right_self_energy, left_self_energy = self_energy_lead(fermi_energy, h00, h01, width, length)
hamiltonian = matrix_center(width, length)
green = np.linalg.inv(fermi_energy*np.identity(width*length)-hamiltonian-left_self_energy-right_self_energy)
right_self_energy = (right_self_energy - right_self_energy.transpose().conj())*1j
left_self_energy = (left_self_energy - left_self_energy.transpose().conj())*1j
G_n = np.imag(np.dot(np.dot(green, left_self_energy), green.transpose().conj()))
return G_n
if __name__ == '__main__':
main()当费米能fermi_energy=0时，计算结果：
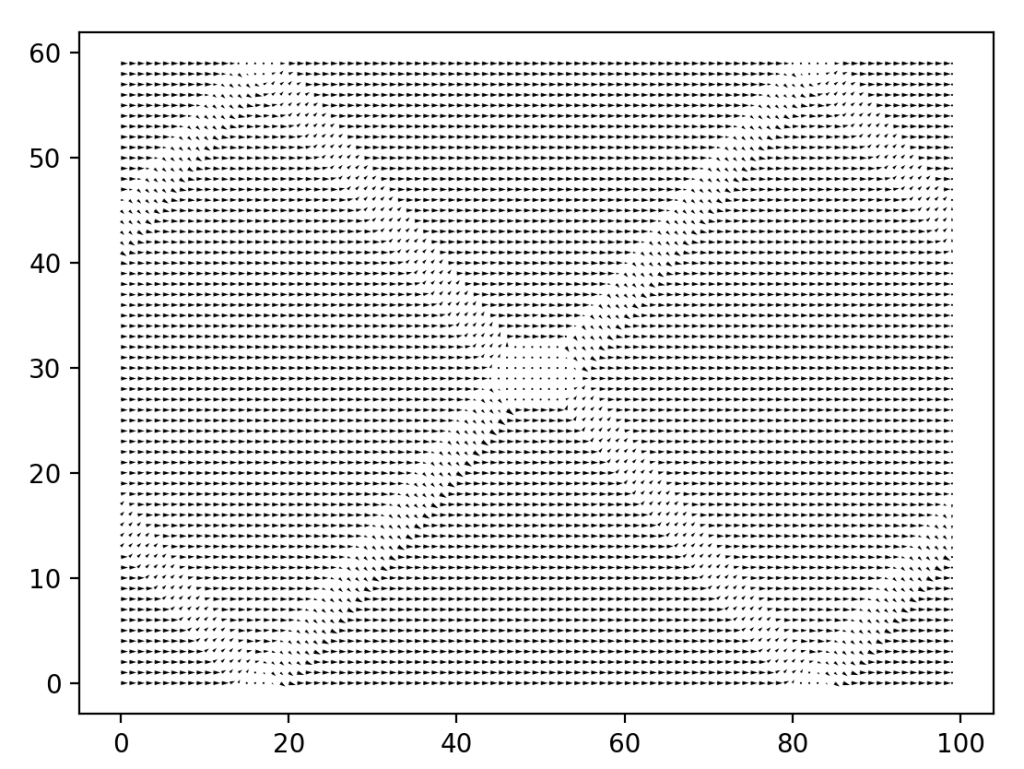
二、使用Guan软件包计算
Guan官网：https://py.guanjihuan.com/。
程序和以上相同，只是通过软件包写得更加简洁。计算结果相同。
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/3888
"""
import numpy as np
import matplotlib.pyplot as plt
import time
import guan
def matrix_00(width=10): # 电极元胞内跃迁，width不赋值时默认为10
h00 = np.zeros((width, width))
for width0 in range(width-1):
h00[width0, width0+1] = 1
h00[width0+1, width0] = 1
return h00
def matrix_01(width=10): # 电极元胞间跃迁，width不赋值时默认为10
h01 = np.identity(width)
return h01
def matrix_LC(width=10, length=300): # 左电极跳到中心区
h_LC = np.zeros((width, width*length))
for width0 in range(width):
h_LC[width0, width0] = 1
return h_LC
def matrix_CR(width=10, length=300): # 中心区跳到右电极
h_CR = np.zeros((width*length, width))
for width0 in range(width):
h_CR[width*(length-1)+width0, width0] = 1
return h_CR
def matrix_center(width=10, length=300): # 中心区哈密顿量
hamiltonian = np.zeros((width*length, width*length))
for length0 in range(length-1):
for width0 in range(width):
hamiltonian[width*length0+width0, width*(length0+1)+width0] = 1 # 长度方向跃迁
hamiltonian[width*(length0+1)+width0, width*length0+width0] = 1
for length0 in range(length):
for width0 in range(width-1):
hamiltonian[width*length0+width0, width*length0+width0+1] = 1 # 宽度方向跃迁
hamiltonian[width*length0+width0+1, width*length0+width0] = 1
# 中间加势垒
for j0 in range(6):
for i0 in range(6):
hamiltonian[width*(int(length/2)-3+j0)+int(width/2)-3+i0, width*(int(length/2)-3+j0)+int(width/2)-3+i0]= 1e8
return hamiltonian
def main():
start_time = time.time()
fermi_energy = 0
width = 60
length = 100
h00 = matrix_00(width)
h01 = matrix_01(width)
h_LC = matrix_LC(width, length)
h_CR = matrix_CR(width, length)
hamiltonian = matrix_center(width, length)
G_n = guan.electron_correlation_function_green_n_for_local_current(fermi_energy, h00, h01, h_LC, h_CR, hamiltonian)
direction_x = np.zeros((width, length))
direction_y = np.zeros((width, length))
for length0 in range(length-1):
for width0 in range(width):
direction_x[width0, length0] = G_n[width*length0+width0, width*(length0+1)+width0]
for length0 in range(length):
for width0 in range(width-1):
direction_y[width0, length0] = G_n[width*length0+width0, width*length0+width0+1]
X, Y = np.meshgrid(range(length), range(width))
plt.quiver(X, Y, direction_x, direction_y)
plt.show()
end_time = time.time()
print('运行时间=', end_time-start_time)
if __name__ == '__main__':
main()三、使用Kwant软件包计算
Kwant官网：https://kwant-project.org/。
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/3888
"""
import kwant
def make_system():
a = 1
lat = kwant.lattice.square(a, norbs=1) # 创建晶格，方格子
syst = kwant.Builder()
t = 1.0
W = 60 # 中心体系宽度
L = 100 # 中心体系长度
# 给中心体系赋值
for i in range(L):
for j in range(W):
syst[lat(i, j)] = 0
if j > 0:
syst[lat(i, j), lat(i, j-1)] = -t # hopping in y-direction
if i > 0:
syst[lat(i, j), lat(i-1, j)] = -t # hopping in x-direction
if 47<=i<53 and 27<=j<33: # 势垒
syst[lat(i, j)] = 1e8
# 电极
lead = kwant.Builder(kwant.TranslationalSymmetry((-a, 0)))
lead[(lat(0, j) for j in range(W))] = 0
lead[lat.neighbors()] = -t # 用neighbors()方法
syst.attach_lead(lead) # 左电极
syst.attach_lead(lead.reversed()) # 用reversed()方法得到右电极
# 制作结束
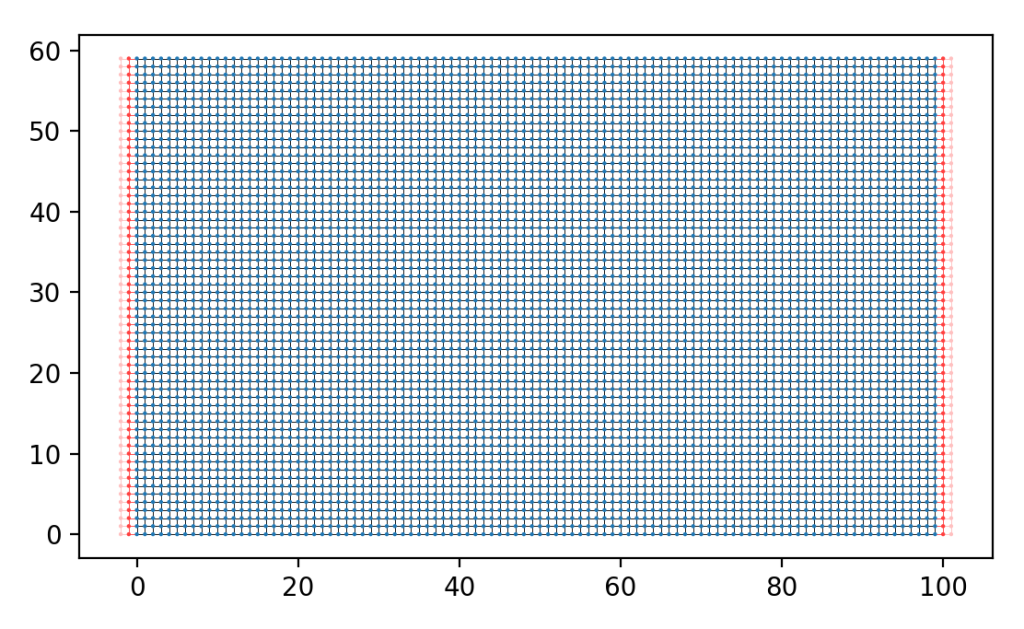
kwant.plot(syst)
syst = syst.finalized()
return syst
def main():
syst = make_system()
psi = kwant.wave_function(syst)(0)[29]
current = kwant.operator.Current(syst)(psi)
kwant.plotter.current(syst, current)
if __name__ == '__main__':
main()选择中间能级的波函数：psi = kwant.wave_function(syst)(0)[29]，计算结果：
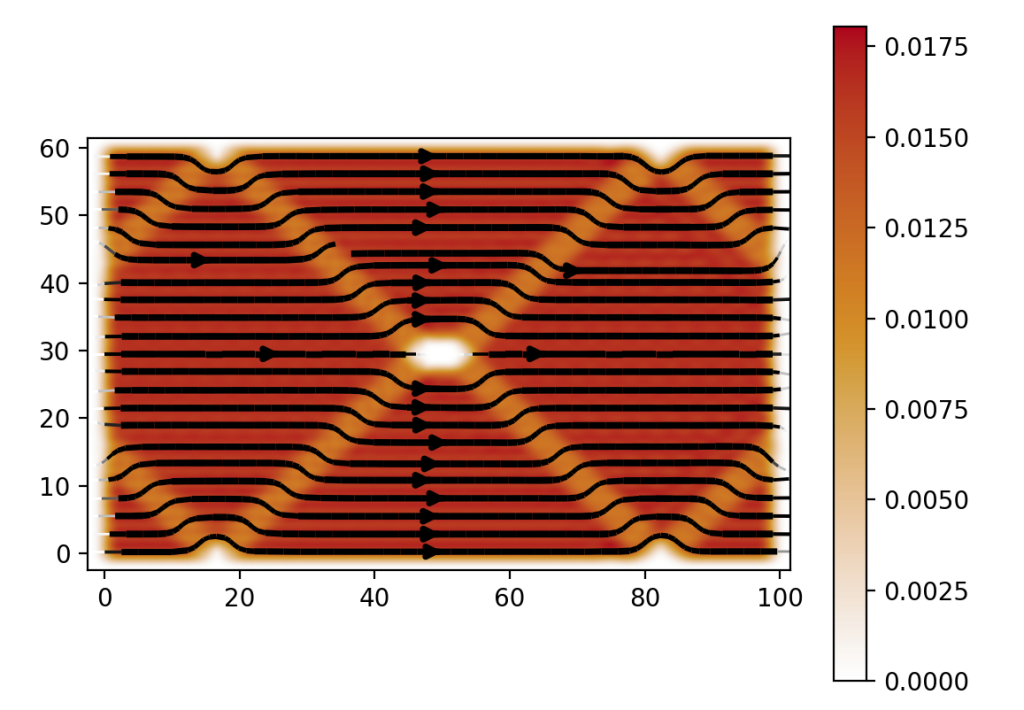
参考资料：
[1] Quantum blockade and loop currents in graphene with topological defects
[2] Numerical study of the topological Anderson insulator in HgTe/CdTe quantum wells
【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】
关老师，计算完G_n后，为什么提取G_n中的那些特定元素加以计算就可以代表i到j之间的电流流向呢？比如length0=1，width0等于1时提取的时G_n(1,5),它可以代表x方向第一个格点的电流强度，这是为什么呢？
假设width为4
因为写哈密顿量的时候，原子编号顺序是按照竖向数的，第一列是1，2，3，4，第二列是5，6，7，8，所以(1，5)就代表第一个格点的向右的电流强度。如果编号顺序是其他的，这时候哈密顿量的形式也会发生变化，那么就不一定是（1，5）了。
关老师，那如果用dyson方程将G_n每层格林函数迭代出来，并没有用到最后大矩阵的哈密顿直接求逆，应该怎么在G_n中取元素代表电流方向呢
我不确定计算量会减少多少，因为这里不只是需要计算格林函数对角矩阵上的元素，还需要计算其他非对角矩阵的元素。可以肯定的是内存占用会小很多，同时算法也会复杂很多。
如果使用Dyson方程计算格林函数，需要在具体某个分块矩阵中去提取电流信息，这和格林函数整体的方法是一样的。
可以参考：
格林函数中Dyson方程的数值验证（附Python代码）、
使用Dyson方程迭代方法计算态密度（附Python代码）、
使用Dyson方程计算格林函数的对角分块矩阵（第二种方法）。
好的，谢谢您
关老师，想问一下，在matlab没有kwant，怎么实现局域电流的计算呢
如果matlab没有对应的软件包，那就只能根据公式自己编写一个实现代码。
关老师，有一个问题。就是您在本篇的part1代码中的，HLC和HCR矩阵，维度是w×(w*l)的，但是您另外一片篇算电导的代码中就是的h00和h01，维度是w×w。 不过因为HCL中有一大部分都是0，好像不影响。 但是您这篇文章中这么写的原因是什么呢？有特别的含义吗？
是的，对于自能的计算是没影响，大部分的矩阵元是零。这里之所以要扩大维度，是因为是要计算中心区的整体格林函数，从而获取电流信息，而不是只计算某个分块矩阵的格林函数。这时候，电极自能的矩阵维度要和中心区的整体格林函数维度保持一致，才可以运算。
理解了，因为中心区gf是(l*w)×（l*w）的。 不过您这边用的是直接求逆计算格林函数。如果使用迭代的话是否矩阵维度就都减小了呢？也就不用HLC这样的扩大维度的矩阵了？
是可以用迭代的方法进行计算，计算效率会高很多。但算法会比较复杂，因为算局域电流时好像不只是需要算格林函数的对角分块矩阵，可能还需要算格林函数的次对角分块矩阵。
格林函数的对角分块矩阵的计算可以参考这两篇：使用Dyson方程迭代方法计算态密度（附Python代码）、使用Dyson方程计算格林函数的对角分块矩阵（第二种方法）。
格林函数的次对角分块矩阵目前我还没去实现，感兴趣也可以试着用戴森方程去推导一下。
博主您好，我想问一下如果用第三种方法Kwant软件包计算的时候，图右侧颜色标尺的数值范围用kwant要如何修改？
我对Kwant不大了解，你可以查查官方的文档
好的 谢谢~
请问一下，关老师，您的局域电流的横纵坐标分别是？
就是在二维平面内的坐标，假设为：0,1,2,3,4,……
您好，请问利用格林函数求解局域电流有参考文献嘛 或者编程前的公式？
公式我是根据本篇博文底部给出的参考资料。可以在此基础上继续搜相关的文献或公式的原始文献。