1. 表象
定义两个表象的正交完备归一基:
表象A: 正交完备归一基矢为![]() ,满足内积
,满足内积![]()
表象B: 正交完备归一基矢为![]() ,满足内积
,满足内积![]()
表象B中的任意基矢可以用A表象的基矢来表示,即
![]()
其中,![]() ,也就是得到表象变换矩阵
,也就是得到表象变换矩阵![]() 。可证明矩阵
。可证明矩阵![]() 是幺正矩阵。
是幺正矩阵。
2. 波函数的表象变换
波函数![]() 在A表象中:
在A表象中:
![]()
其中,![]() 。
。
波函数![]() 在B表象中:
在B表象中:
![]()
其中,![]() 。
。
有以下关系:
![]()
所以,![]()
3. 算符的表象变换
算符![]() 在表象A中:
在表象A中:![]()
算符![]() 在表象B中:
在表象B中:![]()
有关系:
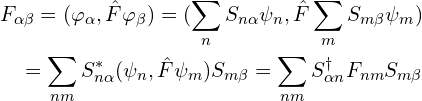
所以,![]()
参考资料:
[1] 季燕江《量子力学讲义》
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】
你好,我有几个问题想要请教您:
一、表象那 S_{n\alpha}的下标是指标识矩阵的,标识哪个\psi_n变换到哪个\phi_{\alpha}的吧,不是指某个矩阵中某个矩阵元,请问是这样吗?
二、S_{n\alpha}等于那两个波函数内积,内积不是得到一个数吗,为什么会得到一个矩阵呀请问?
三、我看见幺正矩阵的性质有一个是S_{m\alpha}^*S_{n\alpha} = I \delta_{nm} 请问这个如何证明啊 ?
如能解答,十分感谢
(1)S_{n\alpha}是表示S矩阵的矩阵元,这个求和的过程其实就是矩阵和向量乘积的过程。
(2)内积后是一个数,不同下标的向量的内积作为矩阵元,组成一个矩阵。
(3)这个性质好像就是幺正矩阵的定义吧,不用证明。可以看看网上资料或线性代数相关的数学书。