1. 单位矩阵:
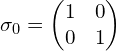
2. 泡利矩阵:
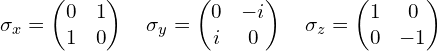
3. 泡利矩阵性质
![]()
![]()
![]()
![]()
对易关系:
![]()
![]()
![]()
反对易关系:
![]()
![]()
![]()
4. 矩阵的张量积(或称为Kronecker积)的定义:

该图片来源于参考资料【2】
也就是将“张量积符号后面的那个矩阵”扔到“张量积符号前面那个矩阵”的各个元素中。
需要说明的是:
- Kronecker积是张量积的特殊形式[3]。
- 在物理中说直积,通常讲的就是张量积。但在数学上直积和张量积还是有区别的,看参考资料[4]。
5. 泡利矩阵的张量积(两套矩阵的符号分别是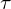 和
和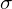 ,空白处代表零元素):
,空白处代表零元素):
(1)张量积符号前面是![]() :
:
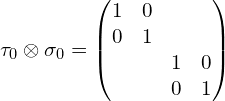
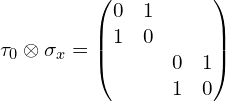
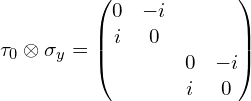
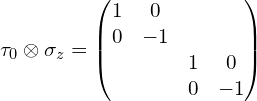
(2)张量积符号前面是![]() :
:
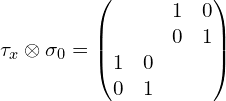
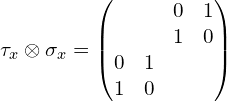
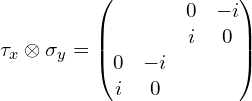
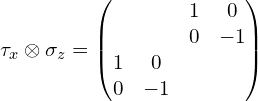
(3)张量积符号前面是![]() (这里为了更直观些,中间多写了一步):
(这里为了更直观些,中间多写了一步):
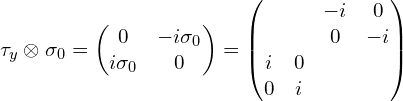
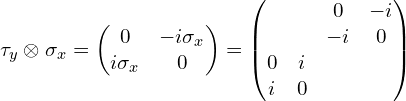
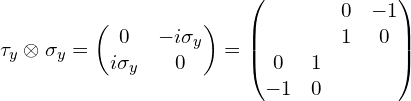
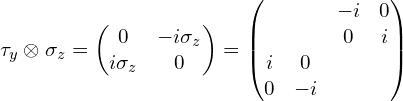
(4)张量积符号前面是![]() (这里为了更直观些,中间多写了一步) :
(这里为了更直观些,中间多写了一步) :
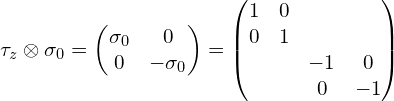
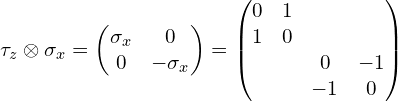
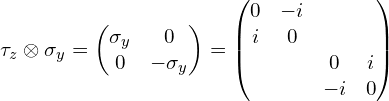
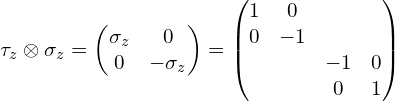
参考资料:
[1] 百度百科:泡利矩阵
[2] 百度文库:矩阵直积
[3] 百度百科:克罗内克积
[4] [张量系列DLC] 直积和张量积有何区别? 矩阵和矩阵的张量积怎么还是个矩阵?
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】
师兄您好,请教一下如何判断泡利矩阵张量积之间的对易与反对易关系呀?谢谢师兄
如果要证明的话,把泡利矩阵张量积代入对易或反对易表达式,从头一步步计算下。如果图方便,可以查一些教材等资料。