常用的泰勒近似

泰勒公式：

$\begin{aligned} f(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2 \\ +\cdots+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n+o((x-x_0)^n) \end{aligned}$

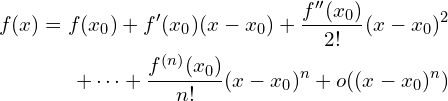
麦克劳林公式（泰勒公式的特殊形式，在零点展开）[1,2]：

$f(x)=f(0)+f'(0)x+\frac{f''(0)}{2!}x^2+\cdots+\frac{f^{(n)}(0)}{n!}x^n+o(x^n)$

常见函数的展开（麦克劳林展开）：

$e^x=1+\frac{1}{1!}x+\frac{1}{2!}x^2+\frac{1}{3!}x^3+o(x^3)$

$ln(1+x)=x-\frac{1}{2}x^2+\frac{1}{3!}x^3+o(x^3)$

$sin(x)=x-\frac{1}{3!}x^3+\frac{1}{5!}x^5+o(x^5)$

$cos(x)=1-\frac{1}{2!}x^2+\frac{1}{4!}x^4+o(x^4)$

$\frac{1}{1-x}=1+x+x^2+x^3+o(x^3)$

$\begin{aligned}(1+x)^\alpha=1&+\frac{\alpha}{1!}x+\frac{\alpha(\alpha-1)}{2!}x^2\\&+\frac{\alpha(\alpha-1)(\alpha-2)}{3!}x^3+o(x^3)\end{aligned}$

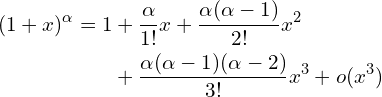
物理中一般取到一阶项或者取到二阶项，如：

$sin(x) \approx x$

$cos(x) \approx 1-\frac{1}{2}x^2$

$\frac{1}{1-x}\approx 1+x$

二元函数的泰勒展开如下所示[1]：

参考资料：

[1] 《数学分析第四版下册》华东师范大学数学系编

6,862 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】

2 thoughts on “常用的泰勒近似”

你好，泰勒展开到二次项，sin(x)+sin(x/2) = x+x/2，这个式子能这样算吗？

Published by guanjihuan