二维离散ky能带的叠加和宽度为Ny的条带能带的关系（附Python代码）

在物理上，宽度为Ny的条带能带应该要接近于二维离散 ky 能带的叠加。本篇想通过代码例子，看它们之间是完全相等，还是仅仅在某种程度上的接近。

首先给出自己的猜想，大概率是对的：（1）在周期性边界条件下，两者是完全等价的。只是要选对离散的 ky 值，但找到对应的离散 ky 值是个难点。（2）在开放边界条件下，两者不完全等价。当 Ny 较大时，也会接近二维离散ky能带的叠加，但需要额外加上边缘态。

需要说明的是：

• 本篇没有给出正确的离散 ky 值，即：黑色实线（二维的多个 ky 截面能带的叠加）和黄色点线（周期边界条件下的条带能带）没有完全重合，因此无法直接在数值上进行验证。如果找到正确的离散 ky 值，黑色实线应该会和黄色点线完全重合。红色的虚线是开放边界条件下的能带。
• 大概思路是：要找到 Ny 值和 ky 数组之间的关系，但还不清楚在理论上是否可行，即 Ny 值是否已经包含了 ky 数组的全部信息。如果有知道怎么找到正确的离散 ky 值，可留言或联系我讨论。

之前已经有给出一些能带图：

• 准一维方格子能带图（附Python代码）
• 石墨烯哈密顿量与能带图（附Python代码）
• Haldane模型哈密顿量与能带图（附Python代码）

本篇使用 Guan 软件包（http://py.guanjihuan.com，版本>=0.0.109）来写代码，调用一些常用的函数，而不是重复书写，这样会简洁一些。函数的具体内容可通过 Guan 软件包的源代码来查看。

一、方格子

Python代码：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/22691
"""


import guan
import numpy as np
import functools


# 2D square lattice
k1_array = np.linspace(-np.pi, np.pi, 100)
k2_array = np.linspace(-np.pi, np.pi, 100)
eigenvalue_array = guan.calculate_eigenvalue_with_two_parameters(k1_array, k2_array, guan.hamiltonian_of_square_lattice)
guan.plot_3d_surface(k1_array, k2_array, eigenvalue_array, xlabel='kx', ylabel='ky', zlabel='E')


# 2D square lattice for discrete ky array
Ny = 10
ky_array = np.linspace(-np.pi, np.pi, Ny) # important
print(ky_array)

kx_array = np.linspace(-np.pi, np.pi, 100)
i0 = 0
for ky in ky_array:
    hamiltonian_function = functools.partial(guan.hamiltonian_of_square_lattice, k2=ky)
    eigenvalue_array = guan.calculate_eigenvalue_with_one_parameter(kx_array, hamiltonian_function)
    if i0 == 0:
        eigenvalue_array_for_discrete_ky = eigenvalue_array
    else:
        eigenvalue_array_for_discrete_ky = np.append(eigenvalue_array_for_discrete_ky, eigenvalue_array, axis=1)
    i0 += 1


# 1D square ribbon
hamiltonian_function = functools.partial(guan.hamiltonian_of_square_lattice_in_quasi_one_dimension, N=Ny)
eigenvalue_array_2 = guan.calculate_eigenvalue_with_one_parameter(kx_array, hamiltonian_function)


# 1D square ribbon with periodic boundary condition in y direction
hamiltonian_function = functools.partial(guan.hamiltonian_of_square_lattice_in_quasi_one_dimension, N=Ny, period=1)
eigenvalue_array_3 = guan.calculate_eigenvalue_with_one_parameter(kx_array, hamiltonian_function)


# Plot figures
guan.plot_three_array(kx_array, eigenvalue_array_for_discrete_ky, eigenvalue_array_2, eigenvalue_array_3, xlabel='kx', ylabel='E', style_1='-k', style_2='--r', style_3='.y', linewidth_1=3, markersize_2=1, markersize_3=1)

运行结果：

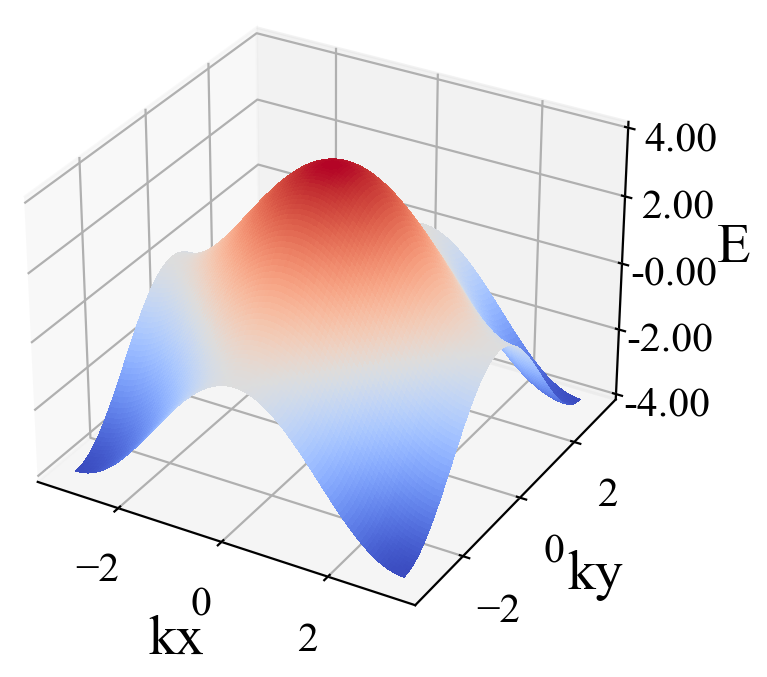
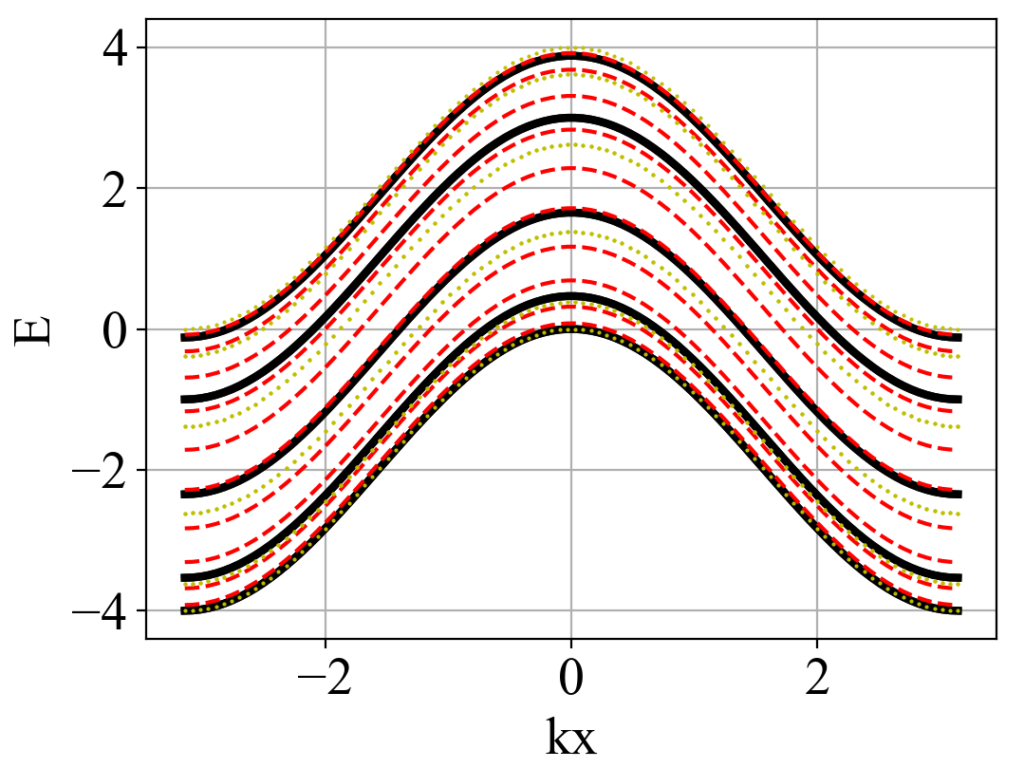
二、石墨烯

Python代码：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/22691
"""


import guan
import numpy as np
import functools


# 2D graphene lattice
k1_array = np.linspace(-2*np.pi, 2*np.pi, 300)
k2_array = np.linspace(-2*np.pi, 2*np.pi, 300)
eigenvalue_array = guan.calculate_eigenvalue_with_two_parameters(k1_array, k2_array, guan.hamiltonian_of_graphene)
guan.plot_3d_surface(k1_array, k2_array, eigenvalue_array, xlabel='kx', ylabel='ky', zlabel='E', rcount=300, ccount=300)


# 2D graphene lattice for discrete ky array
Ny = 5
ky_array = np.linspace(-np.pi, np.pi, Ny*4) # important
print(ky_array)

kx_array = np.linspace(-np.pi, np.pi, 100)
i0 = 0
for ky in ky_array:
    hamiltonian_function = functools.partial(guan.hamiltonian_of_graphene, k2=ky)
    eigenvalue_array = guan.calculate_eigenvalue_with_one_parameter(kx_array, hamiltonian_function)
    if i0 == 0:
        eigenvalue_array_for_discrete_ky = eigenvalue_array
    else:
        eigenvalue_array_for_discrete_ky = np.append(eigenvalue_array_for_discrete_ky, eigenvalue_array, axis=1)
    i0 += 1


# 1D graphene ribbon
hamiltonian_function = functools.partial(guan.hamiltonian_of_graphene_with_zigzag_in_quasi_one_dimension, N=Ny)
eigenvalue_array_2 = guan.calculate_eigenvalue_with_one_parameter(kx_array, hamiltonian_function)


# 1D graphene ribbon with periodic boundary condition in y direction
hamiltonian_function = functools.partial(guan.hamiltonian_of_graphene_with_zigzag_in_quasi_one_dimension, N=Ny, period=1)
eigenvalue_array_3 = guan.calculate_eigenvalue_with_one_parameter(kx_array, hamiltonian_function)


# Plot figures
guan.plot_three_array(kx_array, eigenvalue_array_for_discrete_ky, eigenvalue_array_2, eigenvalue_array_3, xlabel='kx', ylabel='E', style_1='-k', style_2='--r', style_3='.y', linewidth_1=3, markersize_2=3, markersize_3=3)

运行结果：

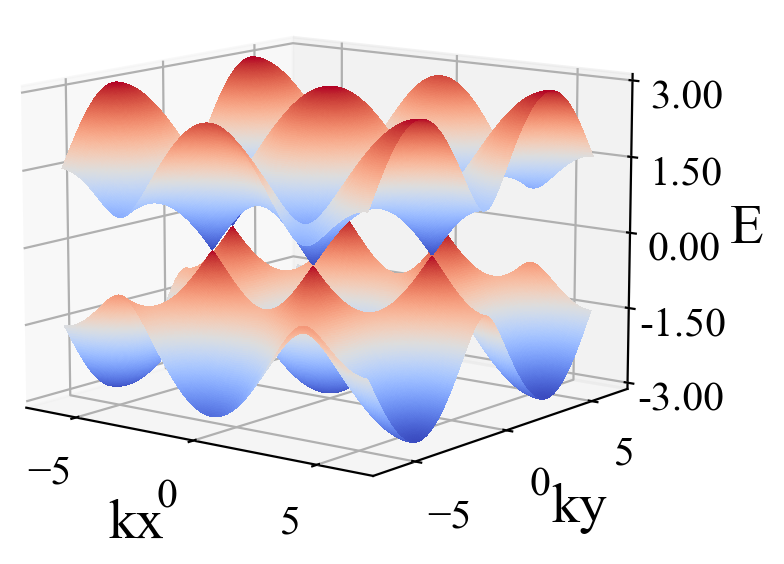
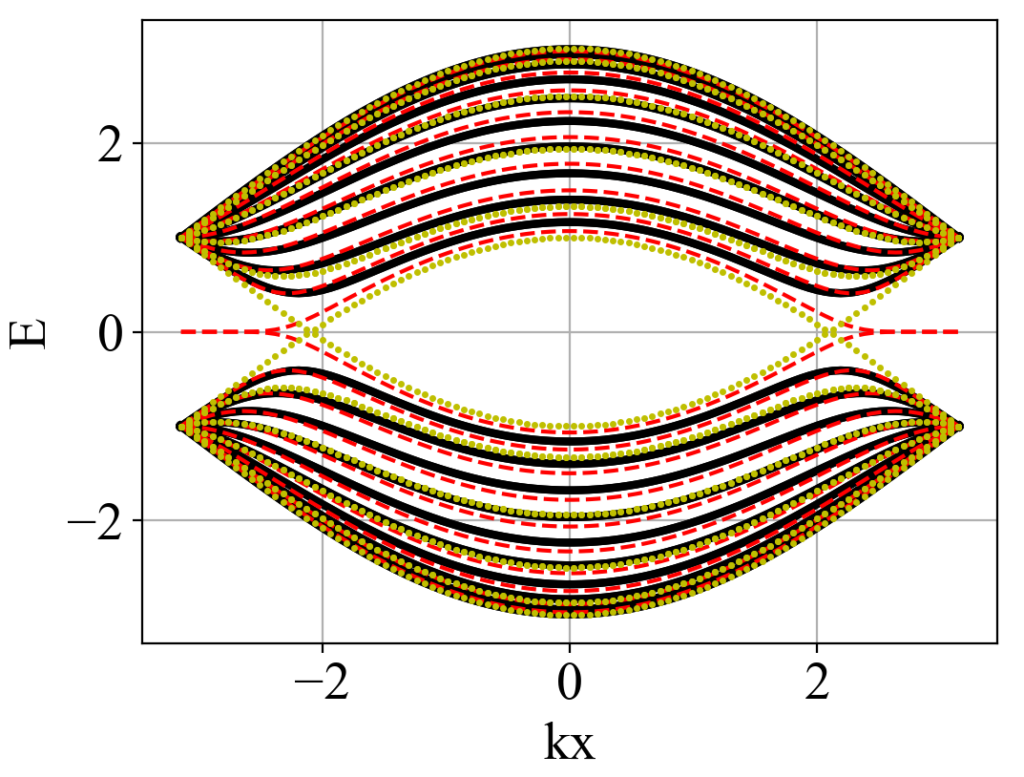
三、Haldane模型

Python代码：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/22691
"""


import guan
import numpy as np
import functools


# 2D Haldane lattice
k1_array = np.linspace(-2*np.pi, 2*np.pi, 100)
k2_array = np.linspace(-2*np.pi, 2*np.pi, 100)
eigenvalue_array = guan.calculate_eigenvalue_with_two_parameters(k1_array, k2_array, guan.hamiltonian_of_haldane_model)
guan.plot_3d_surface(k1_array, k2_array, eigenvalue_array, xlabel='kx', ylabel='ky', zlabel='E')


# 2D Haldane lattice for discrete ky array
Ny = 5
ky_array = np.linspace(-np.pi, np.pi, Ny*4) # important
print(ky_array)

kx_array = np.linspace(-np.pi, np.pi, 100)
i0 = 0
for ky in ky_array:
    hamiltonian_function = functools.partial(guan.hamiltonian_of_haldane_model, k2=ky)
    eigenvalue_array = guan.calculate_eigenvalue_with_one_parameter(-kx_array, hamiltonian_function)
    if i0 == 0:
        eigenvalue_array_for_discrete_ky = eigenvalue_array
    else:
        eigenvalue_array_for_discrete_ky = np.append(eigenvalue_array_for_discrete_ky, eigenvalue_array, axis=1)
    i0 += 1


# 1D Haldane ribbon
hamiltonian_function = functools.partial(guan.hamiltonian_of_haldane_model_in_quasi_one_dimension, N=Ny)
eigenvalue_array_2 = guan.calculate_eigenvalue_with_one_parameter(kx_array, hamiltonian_function)


# 1D Haldane ribbon with periodic boundary condition in y direction
hamiltonian_function = functools.partial(guan.hamiltonian_of_haldane_model_in_quasi_one_dimension, N=Ny, period=1)
eigenvalue_array_3 = guan.calculate_eigenvalue_with_one_parameter(kx_array, hamiltonian_function)


# Plot figures
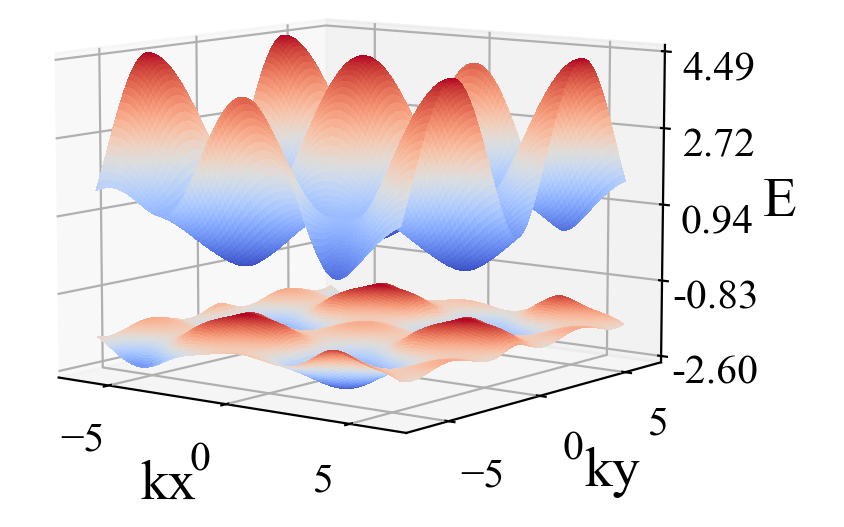
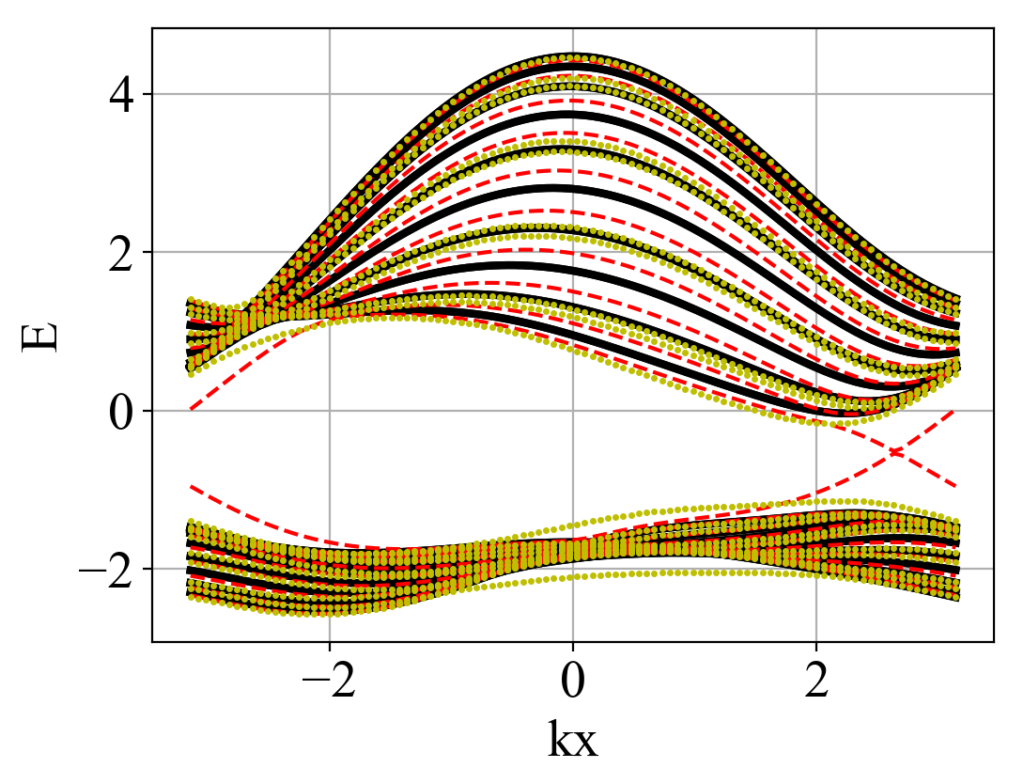
guan.plot_three_array(kx_array, eigenvalue_array_for_discrete_ky, eigenvalue_array_2, eigenvalue_array_3, xlabel='kx', ylabel='E', style_1='-k', style_2='--r', style_3='.y', linewidth_1=3, markersize_2=3, markersize_3=3)

运行结果：

1,523 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】