方格子紧束缚模型中朗道能级的陈数/霍尔电导（附Python代码）

本篇程序主要参考：

• 准一维方格子能带图（附Python代码）
• 佩尔斯替换 Peierls substitution
• 方格子的霍夫斯塔特蝴蝶（附Python代码）
• 陈数Chern number的计算（高效法，附Python/Matlab代码）
• 多端体系的量子输运（附Python代码）
• 介观体系中的Landauer–Büttiker公式
• Python开源项目Guan

本篇代码目录：

1. 二维方格子朗道能级和陈数/霍尔电导
2. 通过六端口的量子输运计算方格子在磁场下的霍尔电导

1. 二维方格子朗道能级和陈数/霍尔电导

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/18306
"""

import numpy as np
from math import *
import cmath
import functools
import guan

def hamiltonian(kx, ky, Ny, B):
    h00 = np.zeros((Ny, Ny), dtype=complex)
    h01 = np.zeros((Ny, Ny), dtype=complex)
    t = 1
    for iy in range(Ny-1):
        h00[iy, iy+1] = t
        h00[iy+1, iy] = t
    h00[Ny-1, 0] = t*cmath.exp(1j*ky)
    h00[0, Ny-1] = t*cmath.exp(-1j*ky)
    for iy in range(Ny):
        h01[iy, iy] = t*cmath.exp(-2*np.pi*1j*B*iy)
    matrix = h00 + h01*cmath.exp(1j*kx) + h01.transpose().conj()*cmath.exp(-1j*kx)
    return matrix


def main():
    Ny = 21

    k_array = np.linspace(-pi, pi, 100)
    H_k = functools.partial(hamiltonian, ky=0, Ny=Ny, B=1/Ny)
    eigenvalue_array = guan.calculate_eigenvalue_with_one_parameter(k_array, H_k)
    guan.plot(k_array, eigenvalue_array, xlabel='kx', ylabel='E', style='k')

    H_k = functools.partial(hamiltonian, Ny=Ny, B=1/Ny)
    chern_number = guan.calculate_chern_number_for_square_lattice_with_efficient_method(H_k, precision=100)
    print(chern_number)
    print(sum(chern_number))


if __name__ == '__main__':
    main()

当Ny=20时，运行结果：

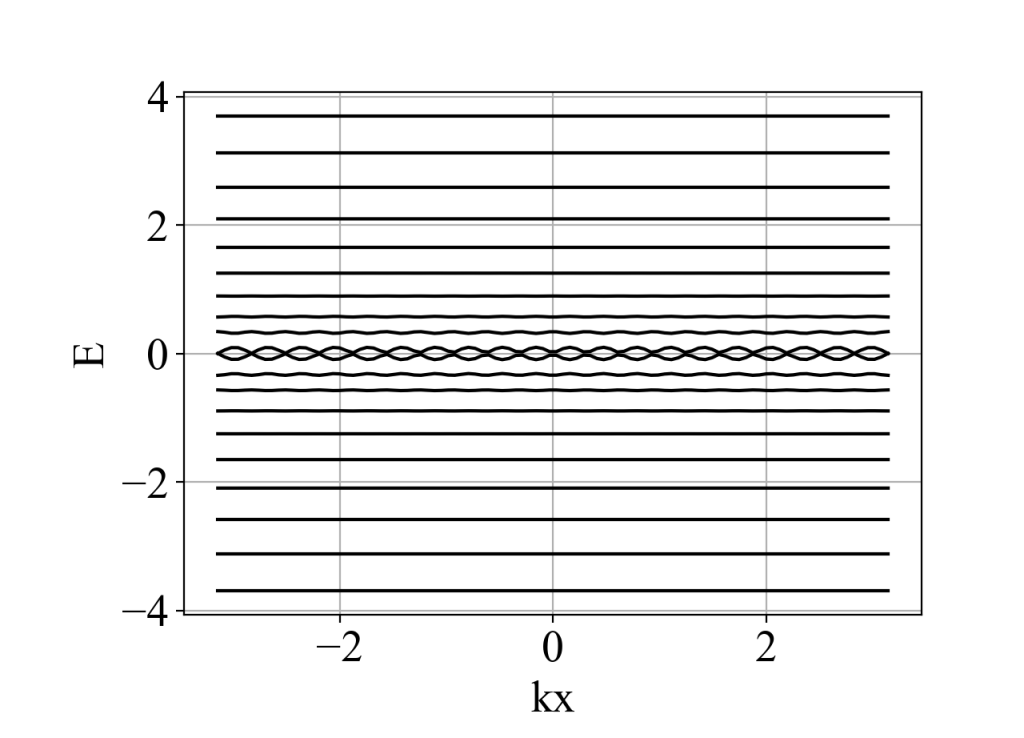
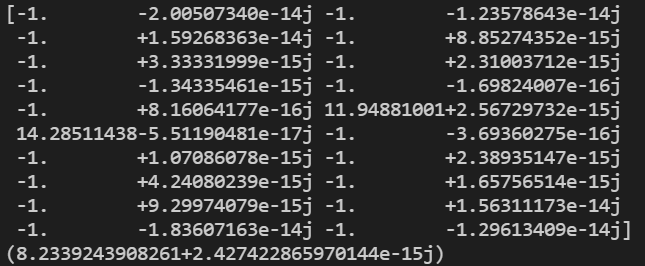
说明：这里计算结果不正确，把所有能带的陈数相加，结果不为零。是因为中间能带部分交叉简并导致的错误。关于简并能带的陈数计算，参考这篇：陈数Chern number的计算（多条能带的Wilson loop方法，附Python代码）。

如果把Ny取为21（奇数），能带不存在部分交叉简并，计算结果正确。运算结果为：

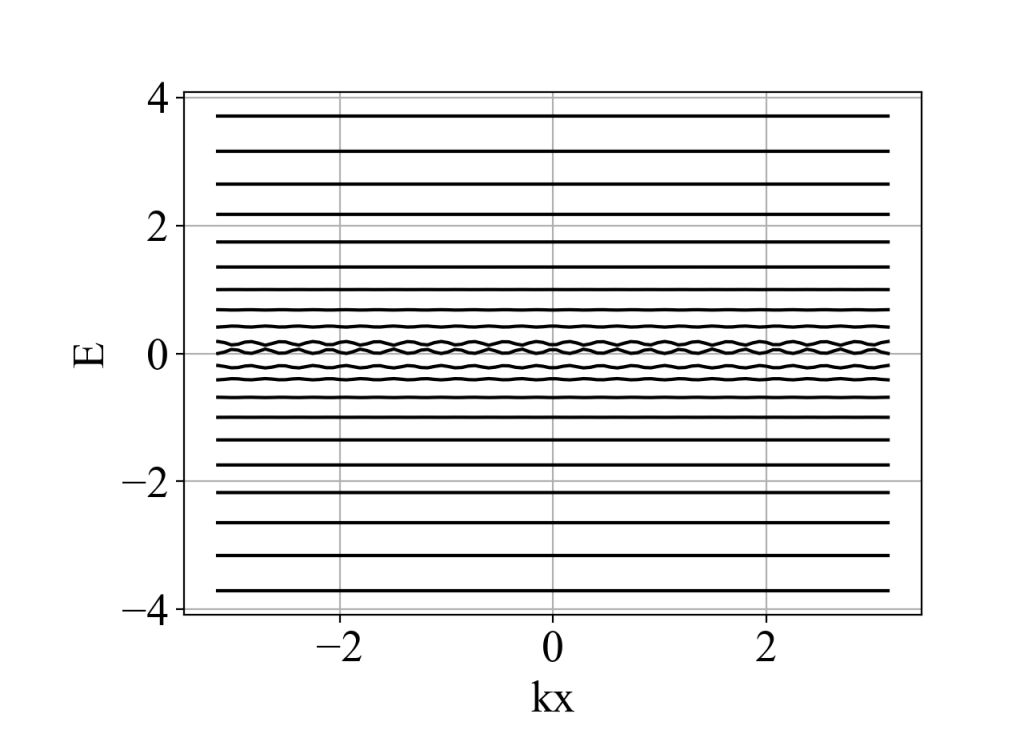
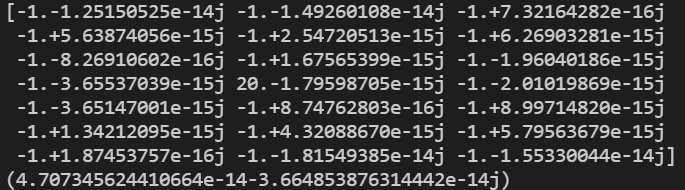
2. 通过六端口的量子输运计算方格子在磁场下的霍尔电导

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/18306
"""

import numpy as np
import time
import cmath
import guan

def get_lead_h00(width):  
    h00 = np.zeros((width, width))
    for i0 in range(width-1):
        h00[i0, i0+1] = 1
        h00[i0+1, i0] = 1
    return h00


def get_lead_h01(width):
    h01 = np.identity(width)
    return h01


def get_center_hamiltonian(Nx, Ny, B):
    h = np.zeros((Nx*Ny, Nx*Ny), dtype=complex)
    for x0 in range(Nx-1):
        for y0 in range(Ny):
            h[x0*Ny+y0, (x0+1)*Ny+y0] = 1*cmath.exp(-2*np.pi*1j*B*y0) # x方向的跃迁
            h[(x0+1)*Ny+y0, x0*Ny+y0] = 1*cmath.exp(2*np.pi*1j*B*y0)
    for x0 in range(Nx):
        for y0 in range(Ny-1):
            h[x0*Ny+y0, x0*Ny+y0+1] = 1 # y方向的跃迁
            h[x0*Ny+y0+1, x0*Ny+y0] = 1 
    return h


def main():
    start_time = time.time()
    width = 21
    length = 72
    fermi_energy_array = np.arange(-4, 4, .05)

    # 中心区的哈密顿量
    H_cetner = get_center_hamiltonian(Nx=length, Ny=width, B=1/width)

    # 电极的h00和h01
    lead_h00 = get_lead_h00(width)
    lead_h01 = get_lead_h01(width)
    
    transmission_12_array = []
    transmission_13_array = []
    transmission_14_array = []
    transmission_15_array = []
    transmission_16_array = []
    transmission_1_all_array = []

    for fermi_energy in fermi_energy_array:
        print(fermi_energy)
        #   几何形状如下所示：
        #               lead2         lead3
        #   lead1(L)                          lead4(R)  
        #               lead6         lead5 

        # 电极到中心区的跃迁矩阵
        h_lead1_to_center = np.zeros((width, width*length), dtype=complex)
        h_lead2_to_center = np.zeros((width, width*length), dtype=complex)
        h_lead3_to_center = np.zeros((width, width*length), dtype=complex)
        h_lead4_to_center = np.zeros((width, width*length), dtype=complex)
        h_lead5_to_center = np.zeros((width, width*length), dtype=complex)
        h_lead6_to_center = np.zeros((width, width*length), dtype=complex)
        move = 10 # the step of leads 2,3,6,5 moving to center
        for i0 in range(width):
            h_lead1_to_center[i0, i0] = 1
            h_lead2_to_center[i0, width*(move+i0)+(width-1)] = 1
            h_lead3_to_center[i0, width*(length-move-1-i0)+(width-1)] = 1
            h_lead4_to_center[i0, width*(length-1)+i0] = 1
            h_lead5_to_center[i0, width*(length-move-1-i0)+0] = 1
            h_lead6_to_center[i0, width*(i0+move)+0] = 1
        # 自能    
        self_energy1, gamma1 = guan.self_energy_of_lead_with_h_lead_to_center(fermi_energy, lead_h00, lead_h01, h_lead1_to_center)
        self_energy2, gamma2 = guan.self_energy_of_lead_with_h_lead_to_center(fermi_energy, lead_h00, lead_h01, h_lead2_to_center)
        self_energy3, gamma3 = guan.self_energy_of_lead_with_h_lead_to_center(fermi_energy, lead_h00, lead_h01, h_lead3_to_center)
        self_energy4, gamma4 = guan.self_energy_of_lead_with_h_lead_to_center(fermi_energy, lead_h00, lead_h01, h_lead4_to_center)
        self_energy5, gamma5 = guan.self_energy_of_lead_with_h_lead_to_center(fermi_energy, lead_h00, lead_h01, h_lead5_to_center)
        self_energy6, gamma6 = guan.self_energy_of_lead_with_h_lead_to_center(fermi_energy, lead_h00, lead_h01, h_lead6_to_center)

        # 整体格林函数
        green = np.linalg.inv(fermi_energy*np.eye(width*length)-H_cetner-self_energy1-self_energy2-self_energy3-self_energy4-self_energy5-self_energy6)

        # Transmission
        transmission_12 = np.trace(np.dot(np.dot(np.dot(gamma1, green), gamma2), green.transpose().conj()))
        transmission_13 = np.trace(np.dot(np.dot(np.dot(gamma1, green), gamma3), green.transpose().conj()))
        transmission_14 = np.trace(np.dot(np.dot(np.dot(gamma1, green), gamma4), green.transpose().conj()))
        transmission_15 = np.trace(np.dot(np.dot(np.dot(gamma1, green), gamma5), green.transpose().conj()))
        transmission_16 = np.trace(np.dot(np.dot(np.dot(gamma1, green), gamma6), green.transpose().conj()))
        transmission_12_array.append(np.real(transmission_12))
        transmission_13_array.append(np.real(transmission_13))
        transmission_14_array.append(np.real(transmission_14))
        transmission_15_array.append(np.real(transmission_15))
        transmission_16_array.append(np.real(transmission_16))
        transmission_1_all_array.append(np.real(transmission_12+transmission_13+transmission_14+transmission_15+transmission_16))
    
    guan.plot(fermi_energy_array, transmission_12_array, xlabel='Fermi energy', ylabel='Transmission_12')
    guan.plot(fermi_energy_array, transmission_13_array, xlabel='Fermi energy', ylabel='Transmission_13')
    guan.plot(fermi_energy_array, transmission_14_array, xlabel='Fermi energy', ylabel='Transmission_14')
    guan.plot(fermi_energy_array, transmission_15_array, xlabel='Fermi energy', ylabel='Transmission_15')
    guan.plot(fermi_energy_array, transmission_16_array, xlabel='Fermi energy', ylabel='Transmission_16')
    guan.plot(fermi_energy_array, transmission_1_all_array, xlabel='Fermi energy', ylabel='Transmission_1_all')
    end_time = time.time()
    print('运行时间=', end_time-start_time)


if __name__ == '__main__':
    main()

运行结果：

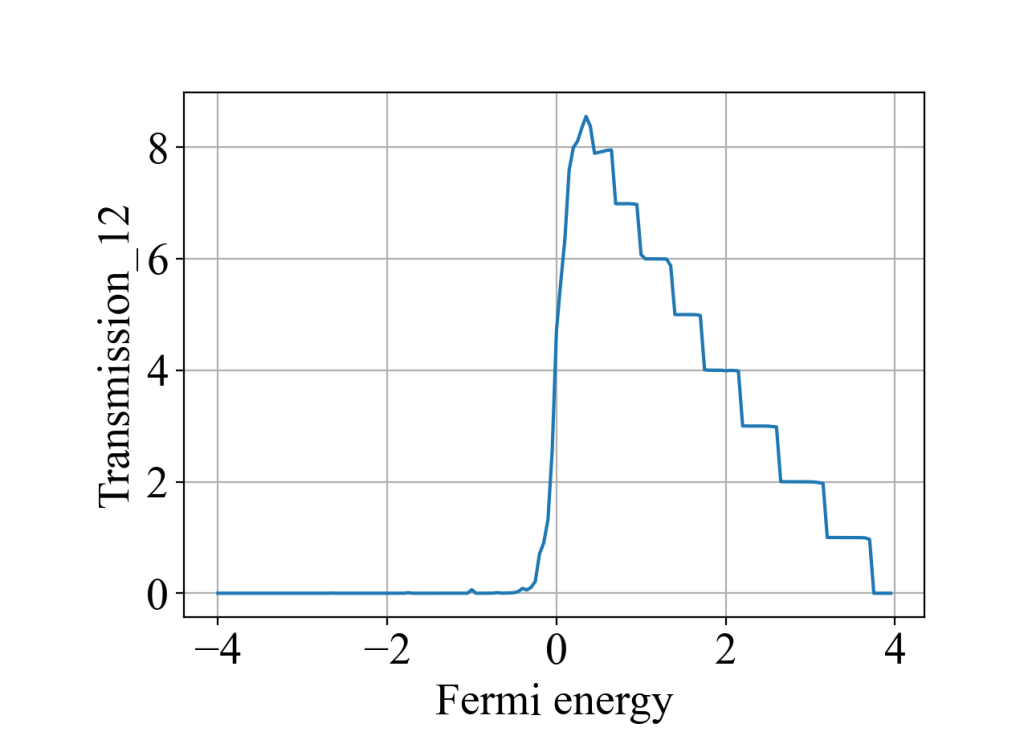
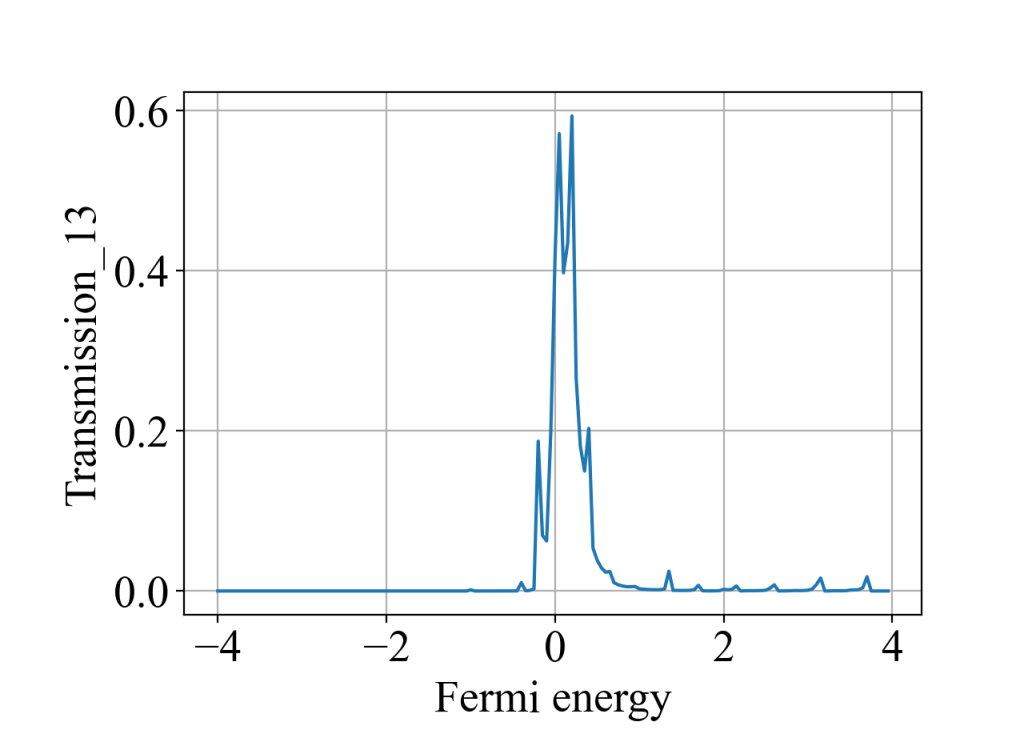
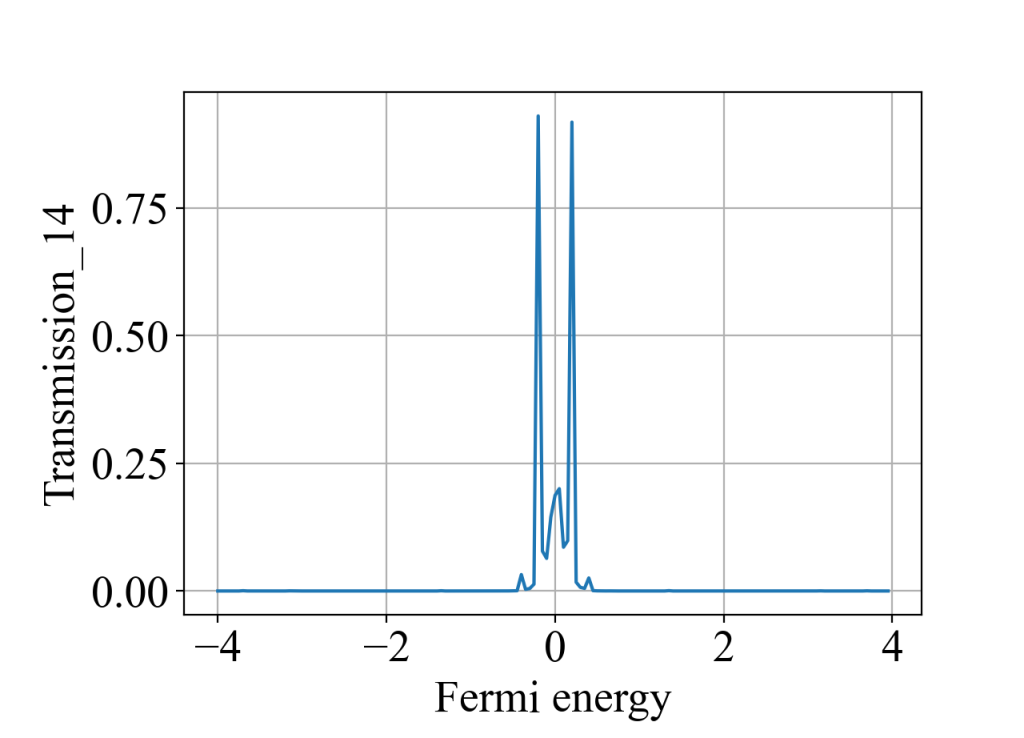
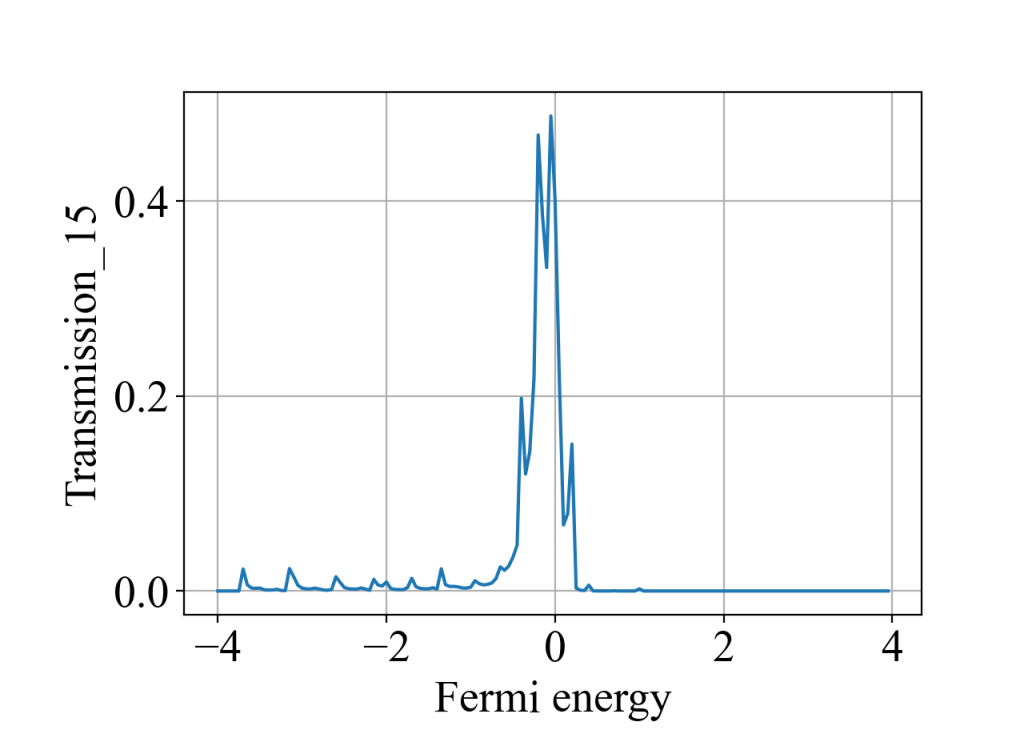
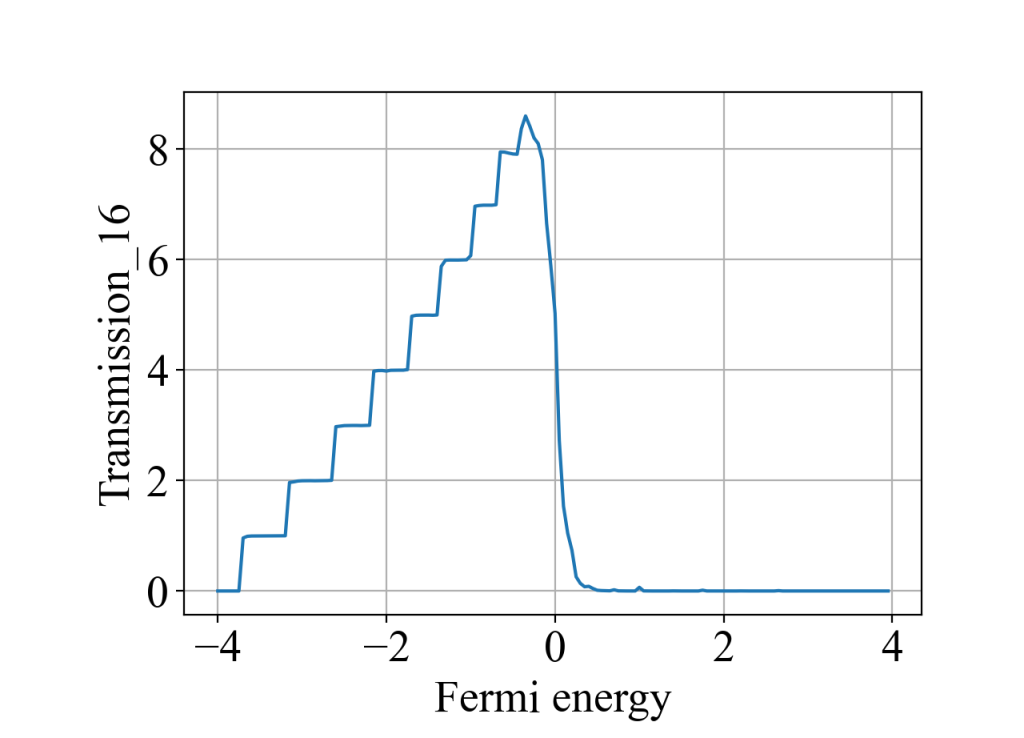
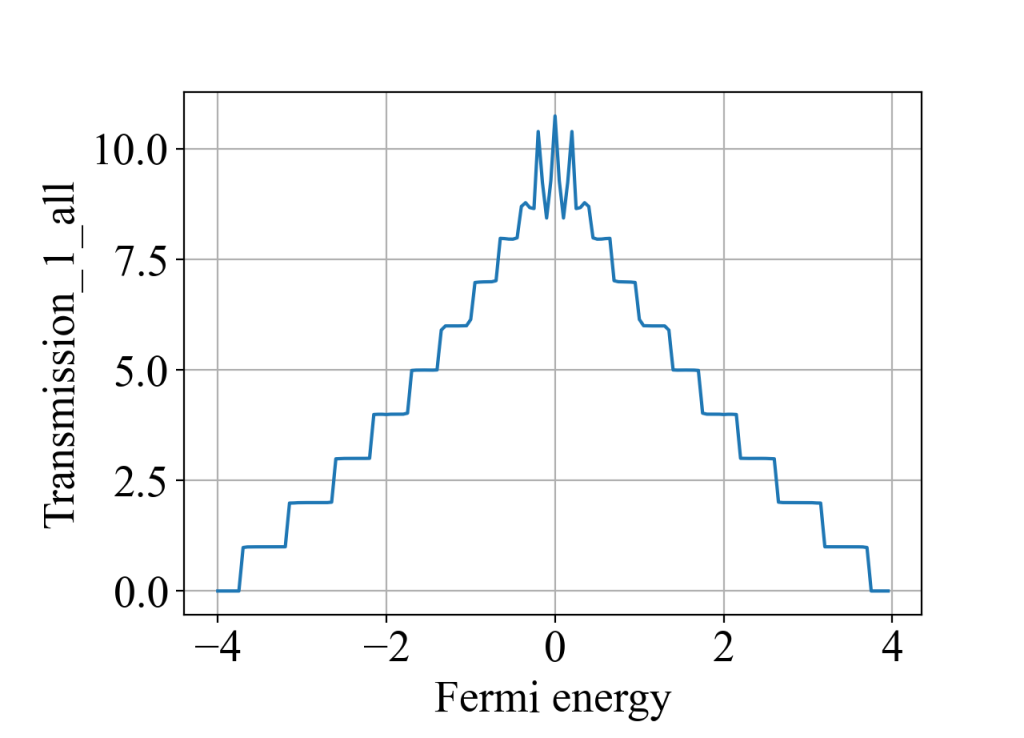
说明1：电极2，3，6，5需要往中间移一点，即move>0，否则相邻电极会相互接触，计算结果出现不了明显的平台。

说明2：对于方格子的情况，通过陈数计算的霍尔电导和通过六端输运计算的霍尔电导在数值上无法完全对应上，这可能是由于前者算的是二维体系，后者算的是准一维体系，存在一定的散射。但总体趋势是一致的：费米能越接近0，霍尔电导值越大，且呈现台阶状。

更多参考资料：

[1] B. Andrei Bernevig - Topological Insulators and Topological Superconductors

[2] A. H. MacDonald - Landau-level subband structure of electrons on a square lattice

[3] Quantized Hall Conductance in a Two-Dimensional Periodic Potential

[4] Route towards Localization for Quantum Anomalous Hall Systems with Chern Number 2

[5] Localization trajectory and Chern-Simons axion coupling for bilayer quantum anomalous Hall systems

2,630 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】