BBH模型的nested Wilson loop高阶不变量（附Python代码）

发布时间：2021年12月9日2022年9月12日

最近修改时间：2022年9月12日

BBH模型和态密度分布参考这篇：BBH高阶拓扑绝缘体模型（附Python代码）。BBH模型和nested Wilson loop公式见参考文献[1-3]。本篇计算的nested Wilson loop仅仅是考虑能带非简并的情况。

一、能带

先画个能带。为了避免重复写代码，可以调用开源软件包Guan中的函数（ https://py.guanjihuan.com）。

Python代码：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/17984
"""

import numpy as np
import cmath
from math import *
import functools

def hamiltonian(kx, ky):  # BBH model
    # label of atoms in a unit cell
    # (2) —— (0)
    #  |      |
    # (1) —— (3)   
    gamma_x = 0.5  # hopping inside one unit cell
    lambda_x = 1   # hopping between unit cells
    gamma_y = gamma_x
    lambda_y = lambda_x
    h = np.zeros((4, 4), dtype=complex)
    h[0, 2] = gamma_x+lambda_x*cmath.exp(1j*kx)
    h[1, 3] = gamma_x+lambda_x*cmath.exp(-1j*kx)
    h[0, 3] = gamma_y+lambda_y*cmath.exp(1j*ky)
    h[1, 2] = -gamma_y-lambda_y*cmath.exp(-1j*ky)
    h[2, 0] = np.conj(h[0, 2])
    h[3, 1] = np.conj(h[1, 3])
    h[3, 0] = np.conj(h[0, 3])
    h[2, 1] = np.conj(h[1, 2]) 
    return h

def main():
    kx = np.arange(-pi, pi, 0.05)
    ky = np.arange(-pi, pi, 0.05)
    eigenvalue_array = calculate_eigenvalue_with_two_parameters(kx, ky, hamiltonian)
    plot_3d_surface(kx, ky, eigenvalue_array, xlabel='kx', ylabel='ky', zlabel='E', title='BBH bands')
    hamiltonian0 = functools.partial(hamiltonian, ky=0) 
    eigenvalue_array = calculate_eigenvalue_with_one_parameter(kx, hamiltonian0)
    plot(kx, eigenvalue_array, xlabel='kx', ylabel='E', title='BBH bands ky=0')

    # import guan
    # eigenvalue_array = guan.calculate_eigenvalue_with_two_parameters(kx, ky, hamiltonian)
    # guan.plot_3d_surface(kx, ky, eigenvalue_array, xlabel='kx', ylabel='ky', zlabel='E', title='BBH bands')
    # hamiltonian0 = functools.partial(hamiltonian, ky=0) 
    # eigenvalue_array = guan.calculate_eigenvalue_with_one_parameter(kx, hamiltonian0)
    # guan.plot(kx, eigenvalue_array, xlabel='kx', ylabel='E', title='BBH bands ky=0')

def calculate_eigenvalue_with_one_parameter(x_array, hamiltonian_function, print_show=0):
    dim_x = np.array(x_array).shape[0]
    i0 = 0
    if np.array(hamiltonian_function(0)).shape==():
        eigenvalue_array = np.zeros((dim_x, 1))
        for x0 in x_array:
            hamiltonian = hamiltonian_function(x0)
            eigenvalue_array[i0, 0] = np.real(hamiltonian)
            i0 += 1
    else:
        dim = np.array(hamiltonian_function(0)).shape[0]
        eigenvalue_array = np.zeros((dim_x, dim))
        for x0 in x_array:
            if print_show==1:
                print(x0)
            hamiltonian = hamiltonian_function(x0)
            eigenvalue, eigenvector = np.linalg.eigh(hamiltonian)
            eigenvalue_array[i0, :] = eigenvalue
            i0 += 1
    return eigenvalue_array

def calculate_eigenvalue_with_two_parameters(x_array, y_array, hamiltonian_function, print_show=0, print_show_more=0):  
    dim_x = np.array(x_array).shape[0]
    dim_y = np.array(y_array).shape[0]
    if np.array(hamiltonian_function(0,0)).shape==():
        eigenvalue_array = np.zeros((dim_y, dim_x, 1))
        i0 = 0
        for y0 in y_array:
            j0 = 0
            for x0 in x_array:
                hamiltonian = hamiltonian_function(x0, y0)
                eigenvalue_array[i0, j0, 0] = np.real(hamiltonian)
                j0 += 1
            i0 += 1
    else:
        dim = np.array(hamiltonian_function(0, 0)).shape[0]
        eigenvalue_array = np.zeros((dim_y, dim_x, dim))
        i0 = 0
        for y0 in y_array:
            j0 = 0
            if print_show==1:
                print(y0)
            for x0 in x_array:
                if print_show_more==1:
                    print(x0)
                hamiltonian = hamiltonian_function(x0, y0)
                eigenvalue, eigenvector = np.linalg.eigh(hamiltonian)
                eigenvalue_array[i0, j0, :] = eigenvalue
                j0 += 1
            i0 += 1
    return eigenvalue_array

def plot(x_array, y_array, xlabel='x', ylabel='y', title='', fontsize=20, labelsize=20, show=1, save=0, filename='a', file_format='.jpg', dpi=300, style='', y_min=None, y_max=None, linewidth=None, markersize=None, adjust_bottom=0.2, adjust_left=0.2): 
    import matplotlib.pyplot as plt
    fig, ax = plt.subplots()
    plt.subplots_adjust(bottom=adjust_bottom, left=adjust_left) 
    ax.plot(x_array, y_array, style, linewidth=linewidth, markersize=markersize)
    ax.grid()
    ax.set_title(title, fontsize=fontsize, fontfamily='Times New Roman')
    ax.set_xlabel(xlabel, fontsize=fontsize, fontfamily='Times New Roman') 
    ax.set_ylabel(ylabel, fontsize=fontsize, fontfamily='Times New Roman') 
    if y_min!=None or y_max!=None:
        if y_min==None:
            y_min=min(y_array)
        if y_max==None:
            y_max=max(y_array)
        ax.set_ylim(y_min, y_max)
    ax.tick_params(labelsize=labelsize) 
    labels = ax.get_xticklabels() + ax.get_yticklabels()
    [label.set_fontname('Times New Roman') for label in labels]
    if save == 1:
        plt.savefig(filename+file_format, dpi=dpi) 
    if show == 1:
        plt.show()
    plt.close('all')

def plot_3d_surface(x_array, y_array, matrix, xlabel='x', ylabel='y', zlabel='z', title='', fontsize=20, labelsize=15, show=1, save=0, filename='a', file_format='.jpg', dpi=300, z_min=None, z_max=None, rcount=100, ccount=100): 
    import matplotlib.pyplot as plt
    from matplotlib import cm
    from matplotlib.ticker import LinearLocator
    matrix = np.array(matrix)
    fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
    plt.subplots_adjust(bottom=0.1, right=0.65) 
    x_array, y_array = np.meshgrid(x_array, y_array)
    if len(matrix.shape) == 2:
        surf = ax.plot_surface(x_array, y_array, matrix, rcount=rcount, ccount=ccount, cmap=cm.coolwarm, linewidth=0, antialiased=False) 
    elif len(matrix.shape) == 3:
        for i0 in range(matrix.shape[2]):
            surf = ax.plot_surface(x_array, y_array, matrix[:,:,i0], rcount=rcount, ccount=ccount, cmap=cm.coolwarm, linewidth=0, antialiased=False) 
    ax.set_title(title, fontsize=fontsize, fontfamily='Times New Roman')
    ax.set_xlabel(xlabel, fontsize=fontsize, fontfamily='Times New Roman') 
    ax.set_ylabel(ylabel, fontsize=fontsize, fontfamily='Times New Roman') 
    ax.set_zlabel(zlabel, fontsize=fontsize, fontfamily='Times New Roman') 
    ax.zaxis.set_major_locator(LinearLocator(5)) 
    ax.zaxis.set_major_formatter('{x:.2f}')  
    if z_min!=None or z_max!=None:
        if z_min==None:
            z_min=matrix.min()
        if z_max==None:
            z_max=matrix.max()
        ax.set_zlim(z_min, z_max)
    ax.tick_params(labelsize=labelsize) 
    labels = ax.get_xticklabels() + ax.get_yticklabels() + ax.get_zticklabels()
    [label.set_fontname('Times New Roman') for label in labels] 
    cax = plt.axes([0.8, 0.1, 0.05, 0.8]) 
    cbar = fig.colorbar(surf, cax=cax)  
    cbar.ax.tick_params(labelsize=labelsize)
    for l in cbar.ax.yaxis.get_ticklabels():
        l.set_family('Times New Roman')
    if save == 1:
        plt.savefig(filename+file_format, dpi=dpi) 
    if show == 1:
        plt.show()
    plt.close('all')

if __name__ == '__main__':
    main()

运行结果：

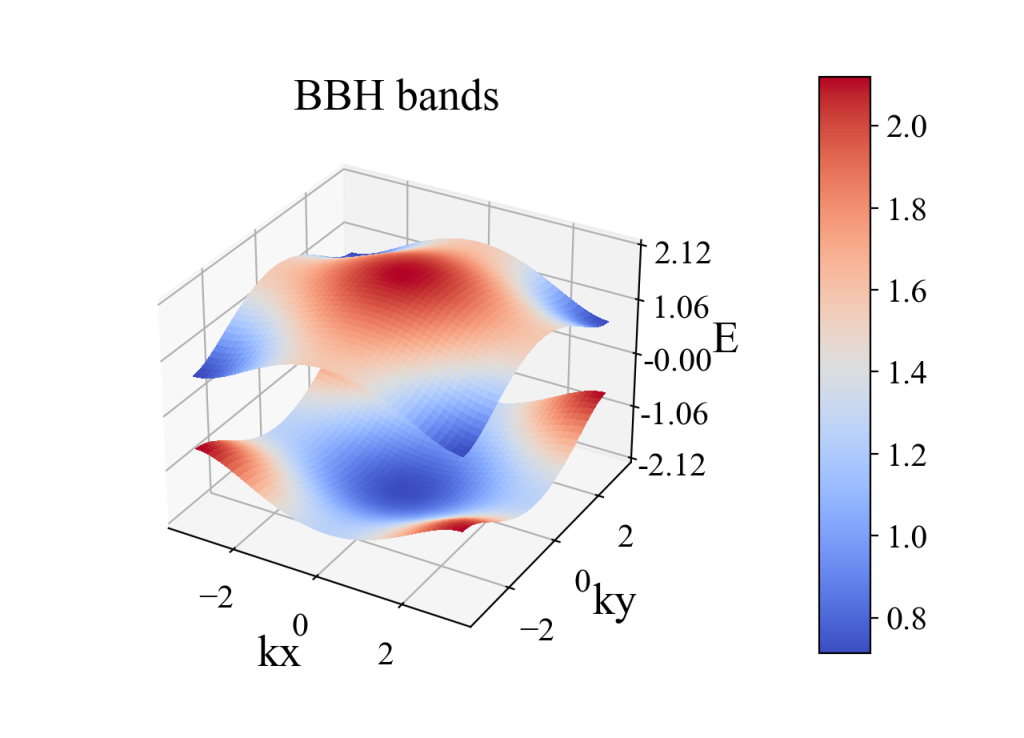
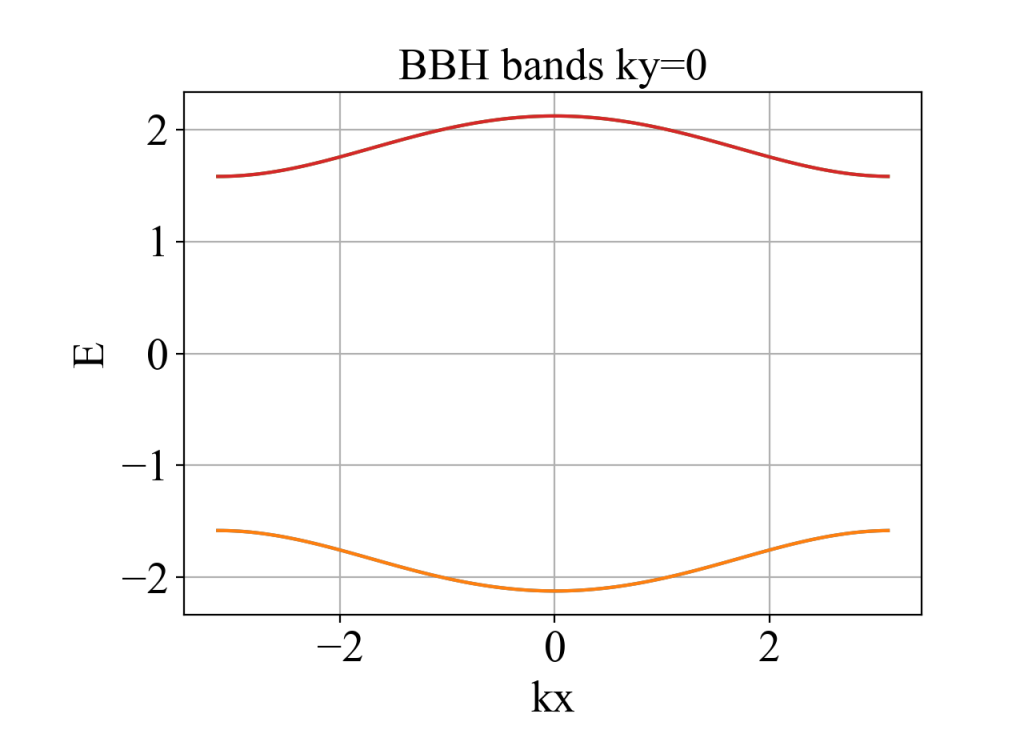
二、Wilson loop

Python代码：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/17984
"""

import numpy as np
import cmath
from math import *

def hamiltonian(kx, ky):  # BBH model
    # label of atoms in a unit cell
    # (2) —— (0)
    #  |      |
    # (1) —— (3)   
    gamma_x = 0.5  # hopping inside one unit cell
    lambda_x = 1   # hopping between unit cells
    gamma_y = gamma_x
    lambda_y = lambda_x
    h = np.zeros((4, 4), dtype=complex)
    h[0, 2] = gamma_x+lambda_x*cmath.exp(1j*kx)
    h[1, 3] = gamma_x+lambda_x*cmath.exp(-1j*kx)
    h[0, 3] = gamma_y+lambda_y*cmath.exp(1j*ky)
    h[1, 2] = -gamma_y-lambda_y*cmath.exp(-1j*ky)
    h[2, 0] = np.conj(h[0, 2])
    h[3, 1] = np.conj(h[1, 3])
    h[3, 0] = np.conj(h[0, 3])
    h[2, 1] = np.conj(h[1, 2]) 
    return h

def main():
    Num_kx = 100
    Num_ky = 100
    kx_array = np.linspace(-pi, pi, Num_kx)
    ky_array = np.linspace(-pi, pi, Num_ky)
    nu_x_array = []
    for ky in ky_array:
        vector1_array = []
        vector2_array = []
        for kx in kx_array:
            eigenvalue, eigenvector = np.linalg.eigh(hamiltonian(kx, ky))
            if kx != pi:
                vector1_array.append(eigenvector[:, 0])
                vector2_array.append(eigenvector[:, 1])
            else:
                # 这里是为了-pi和pi有相同的波函数，使得Wilson loop的值与波函数规范无关。
                vector1_array.append(vector1_array[0])
                vector2_array.append(vector2_array[0])
        W_x_k = np.eye(2, dtype=complex)
        for i0 in range(Num_kx-1):
            F = np.zeros((2, 2), dtype=complex)
            F[0, 0] = np.dot(vector1_array[i0+1].transpose().conj(), vector1_array[i0])
            F[1, 1] = np.dot(vector2_array[i0+1].transpose().conj(), vector2_array[i0])
            F[0, 1] = np.dot(vector1_array[i0+1].transpose().conj(), vector2_array[i0])
            F[1, 0] = np.dot(vector2_array[i0+1].transpose().conj(), vector1_array[i0])
            W_x_k = np.dot(F, W_x_k)
        eigenvalue, eigenvector = np.linalg.eig(W_x_k)
        nu_x = np.log(eigenvalue)/2/pi/1j 
        for i0 in range(2):
            if np.real(nu_x[i0]) < 0:
                nu_x[i0] += 1
        nu_x = np.sort(nu_x)
        nu_x_array.append(nu_x.real)
    plot(ky_array, nu_x_array, xlabel='ky', ylabel='nu_x', style='-', y_min=0, y_max=1)
    # import guan
    # guan.plot(ky_array, nu_x_array, xlabel='ky', ylabel='nu_x', style='-', y_min=0, y_max=1)

def plot(x_array, y_array, xlabel='x', ylabel='y', title='', fontsize=20, labelsize=20, show=1, save=0, filename='a', file_format='.jpg', dpi=300, style='', y_min=None, y_max=None, linewidth=None, markersize=None, adjust_bottom=0.2, adjust_left=0.2): 
    import matplotlib.pyplot as plt
    fig, ax = plt.subplots()
    plt.subplots_adjust(bottom=adjust_bottom, left=adjust_left) 
    ax.plot(x_array, y_array, style, linewidth=linewidth, markersize=markersize)
    ax.grid()
    ax.set_title(title, fontsize=fontsize, fontfamily='Times New Roman')
    ax.set_xlabel(xlabel, fontsize=fontsize, fontfamily='Times New Roman') 
    ax.set_ylabel(ylabel, fontsize=fontsize, fontfamily='Times New Roman') 
    if y_min!=None or y_max!=None:
        if y_min==None:
            y_min=min(y_array)
        if y_max==None:
            y_max=max(y_array)
        ax.set_ylim(y_min, y_max)
    ax.tick_params(labelsize=labelsize) 
    labels = ax.get_xticklabels() + ax.get_yticklabels()
    [label.set_fontname('Times New Roman') for label in labels]
    if save == 1:
        plt.savefig(filename+file_format, dpi=dpi) 
    if show == 1:
        plt.show()
    plt.close('all')

if __name__ == '__main__':
    main()

运行结果：

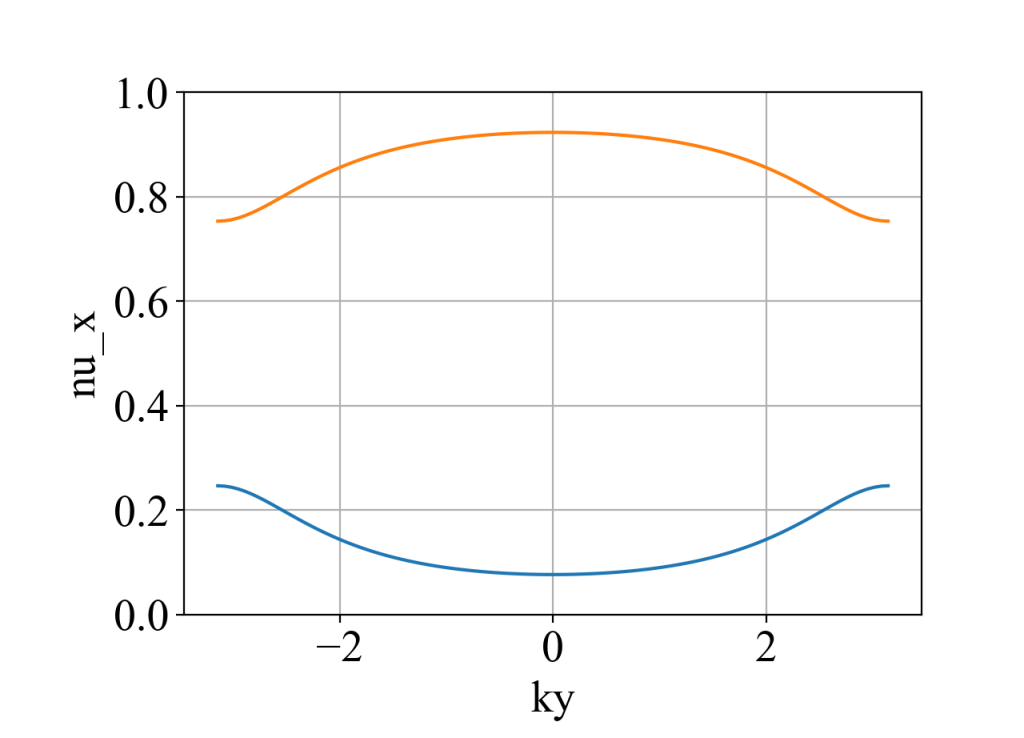
nu_y的计算类似。

三、nested Wilson loop

Python代码（非简并的情况）：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/17984
"""

import numpy as np
import cmath
from math import *

def hamiltonian(kx, ky):  # BBH model
    # label of atoms in a unit cell
    # (2) —— (0)
    #  |      |
    # (1) —— (3)   
    gamma_x = 0.5  # hopping inside one unit cell
    lambda_x = 1   # hopping between unit cells
    gamma_y = gamma_x
    lambda_y = lambda_x
    x_symmetry_breaking_1 = 0.000000000000    # default (not breaking): zero
    x_symmetry_breaking_2 = 1.0000000000001   # default (not breaking): unity
    y_symmetry_breaking_1 = 0.000000000000    # default (not breaking): zero
    y_symmetry_breaking_2 = 1.000000000000    # default (not breaking): unity
    h = np.zeros((4, 4), dtype=complex)
    h[0, 0] = x_symmetry_breaking_1
    h[1, 1] = y_symmetry_breaking_1
    h[2, 2] = y_symmetry_breaking_1
    h[3, 3] = x_symmetry_breaking_1
    h[0, 2] = (gamma_x+lambda_x*cmath.exp(1j*kx))*y_symmetry_breaking_2
    h[1, 3] = gamma_x+lambda_x*cmath.exp(-1j*kx)
    h[0, 3] = gamma_y+lambda_y*cmath.exp(1j*ky)
    h[1, 2] = (-gamma_y-lambda_y*cmath.exp(-1j*ky))*x_symmetry_breaking_2
    h[2, 0] = np.conj(h[0, 2])
    h[3, 1] = np.conj(h[1, 3])
    h[3, 0] = np.conj(h[0, 3])
    h[2, 1] = np.conj(h[1, 2]) 
    return h

def main():
    Num_kx = 30  # for wilson loop and nested wilson loop
    Num_ky = 30  # for wilson loop and nested wilson loop
    Num_kx2 = 20  # plot precision
    Num_ky2 = 20  # plot precision
    kx_array = np.linspace(-pi, pi, Num_kx)
    ky_array = np.linspace(-pi, pi, Num_ky)
    kx2_array = np.linspace(-pi, pi, Num_kx2)
    ky2_array = np.linspace(-pi, pi, Num_ky2)

    # Part I: calculate p_y_for_nu_x
    p_y_for_nu_x_array = []
    for kx in kx2_array:
        print('kx=', kx)
        w_vector_for_nu1_array = []
        vector1_array = []
        vector2_array = []
        i0 = -1
        for ky in ky_array:
            eigenvalue, eigenvector = np.linalg.eigh(hamiltonian(kx, ky))
            if ky != pi:
                vector1_array.append(eigenvector[:, 0])
                vector2_array.append(eigenvector[:, 1])
            else:
                vector1_array.append(vector1_array[0])
                vector2_array.append(vector2_array[0])
        i0=0
        for ky in ky_array:
            if ky != pi:
                nu_x_vector_1, nu_x_vector_2 = get_nu_x_vector(kx_array, ky)
                #  the Wannier band subspaces
                w_vector_for_nu1 =  vector1_array[i0]*nu_x_vector_1[0]+vector2_array[i0]*nu_x_vector_1[1]
                w_vector_for_nu1_array.append(w_vector_for_nu1)
            else:
                w_vector_for_nu1_array.append(w_vector_for_nu1_array[0])
            i0 +=1
        W_y_k_for_nu_x = 1
        for i0 in range(Num_ky-1):
            F_for_nu_x = np.dot(w_vector_for_nu1_array[i0+1].transpose().conj(), w_vector_for_nu1_array[i0])
            W_y_k_for_nu_x = F_for_nu_x*W_y_k_for_nu_x
        p_y_for_nu_x = np.log(W_y_k_for_nu_x)/2/pi/1j
        if np.real(p_y_for_nu_x) < 0:
            p_y_for_nu_x += 1
        p_y_for_nu_x_array.append(p_y_for_nu_x.real) 
        print('p_y_for_nu_x=', p_y_for_nu_x)
    plot(kx2_array, p_y_for_nu_x_array, xlabel='kx', ylabel='p_y_for_nu_x', style='-o', y_min=0, y_max=1)
    # import guan
    # guan.plot(kx2_array, p_y_for_nu_x_array, xlabel='kx', ylabel='p_y_for_nu_x', style='-o', y_min=0, y_max=1)

    # Part II: calculate p_x_for_nu_y
    p_x_for_nu_y_array = []
    for ky in  ky2_array:
        w_vector_for_nu1_array = []
        vector1_array = []
        vector2_array = []
        for kx in kx_array:
            eigenvalue, eigenvector = np.linalg.eigh(hamiltonian(kx, ky))
            if kx != pi:
                vector1_array.append(eigenvector[:, 0])
                vector2_array.append(eigenvector[:, 1])
            else:
                vector1_array.append(vector1_array[0])
                vector2_array.append(vector2_array[0])
        i0 = 0
        for kx in kx_array:
            if kx != pi:
                nu_y_vector_1, nu_y_vector_2 = get_nu_y_vector(kx, ky_array)
                #  the Wannier band subspaces
                w_vector_for_nu1 =  vector1_array[i0]*nu_y_vector_1[0]+vector2_array[i0]*nu_y_vector_1[1]
                w_vector_for_nu1_array.append(w_vector_for_nu1)
            else:
                w_vector_for_nu1_array.append(w_vector_for_nu1_array[0])
            i0 += 1
        W_x_k_for_nu_y = 1
        for i0 in range(Num_ky-1):
            F_for_nu_y = np.dot(w_vector_for_nu1_array[i0+1].transpose().conj(), w_vector_for_nu1_array[i0])
            W_x_k_for_nu_y = F_for_nu_y*W_x_k_for_nu_y
        p_x_for_nu_y = np.log(W_x_k_for_nu_y)/2/pi/1j
        if np.real(p_x_for_nu_y) < 0:
            p_x_for_nu_y += 1
        p_x_for_nu_y_array.append(p_x_for_nu_y.real)
        print('p_x_for_nu_y=', p_x_for_nu_y)
    # print(sum(p_x_for_nu_y_array)/len(p_x_for_nu_y_array))
    plot(ky2_array, p_x_for_nu_y_array, xlabel='ky', ylabel='p_x_for_nu_y', style='-o', y_min=0, y_max=1)
    # import guan
    # guan.plot(ky2_array, p_x_for_nu_y_array, xlabel='ky', ylabel='p_x_for_nu_y', style='-o', y_min=0, y_max=1)

def get_nu_x_vector(kx_array, ky):
    Num_kx = len(kx_array)
    vector1_array = []
    vector2_array = []
    for kx in kx_array:
        eigenvalue, eigenvector = np.linalg.eigh(hamiltonian(kx, ky))
        if kx != pi:
            vector1_array.append(eigenvector[:, 0])
            vector2_array.append(eigenvector[:, 1])
        else:
            vector1_array.append(vector1_array[0])
            vector2_array.append(vector2_array[0])
    W_x_k = np.eye(2, dtype=complex)
    for i0 in range(Num_kx-1):
        F = np.zeros((2, 2), dtype=complex)
        F[0, 0] = np.dot(vector1_array[i0+1].transpose().conj(), vector1_array[i0])
        F[1, 1] = np.dot(vector2_array[i0+1].transpose().conj(), vector2_array[i0])
        F[0, 1] = np.dot(vector1_array[i0+1].transpose().conj(), vector2_array[i0])
        F[1, 0] = np.dot(vector2_array[i0+1].transpose().conj(), vector1_array[i0])
        W_x_k = np.dot(F, W_x_k)
    eigenvalue, eigenvector = np.linalg.eig(W_x_k)
    nu_x = np.log(eigenvalue)/2/pi/1j
    nu_x_vector_1 = eigenvector[:, np.argsort(np.real(nu_x))[0]]
    nu_x_vector_2 = eigenvector[:, np.argsort(np.real(nu_x))[1]]
    return nu_x_vector_1, nu_x_vector_2

def get_nu_y_vector(kx, ky_array):
    Num_ky = len(ky_array)
    vector1_array = []
    vector2_array = []
    for ky in ky_array:
        eigenvalue, eigenvector = np.linalg.eigh(hamiltonian(kx, ky))
        if ky != pi:
            vector1_array.append(eigenvector[:, 0])
            vector2_array.append(eigenvector[:, 1])
        else:
            vector1_array.append(vector1_array[0])
            vector2_array.append(vector2_array[0])
    W_y_k = np.eye(2, dtype=complex)
    for i0 in range(Num_ky-1):
        F = np.zeros((2, 2), dtype=complex)
        F[0, 0] = np.dot(vector1_array[i0+1].transpose().conj(), vector1_array[i0])
        F[1, 1] = np.dot(vector2_array[i0+1].transpose().conj(), vector2_array[i0])
        F[0, 1] = np.dot(vector1_array[i0+1].transpose().conj(), vector2_array[i0])
        F[1, 0] = np.dot(vector2_array[i0+1].transpose().conj(), vector1_array[i0])
        W_y_k = np.dot(F, W_y_k)
    eigenvalue, eigenvector = np.linalg.eig(W_y_k)
    nu_y = np.log(eigenvalue)/2/pi/1j
    nu_y_vector_1 = eigenvector[:, np.argsort(np.real(nu_y))[0]]
    nu_y_vector_2 = eigenvector[:, np.argsort(np.real(nu_y))[1]]
    return nu_y_vector_1, nu_y_vector_2

def plot(x_array, y_array, xlabel='x', ylabel='y', title='', fontsize=20, labelsize=20, show=1, save=0, filename='a', file_format='.jpg', dpi=300, style='', y_min=None, y_max=None, linewidth=None, markersize=None, adjust_bottom=0.2, adjust_left=0.2): 
    import matplotlib.pyplot as plt
    fig, ax = plt.subplots()
    plt.subplots_adjust(bottom=adjust_bottom, left=adjust_left) 
    ax.plot(x_array, y_array, style, linewidth=linewidth, markersize=markersize)
    ax.grid()
    ax.set_title(title, fontsize=fontsize, fontfamily='Times New Roman')
    ax.set_xlabel(xlabel, fontsize=fontsize, fontfamily='Times New Roman') 
    ax.set_ylabel(ylabel, fontsize=fontsize, fontfamily='Times New Roman') 
    if y_min!=None or y_max!=None:
        if y_min==None:
            y_min=min(y_array)
        if y_max==None:
            y_max=max(y_array)
        ax.set_ylim(y_min, y_max)
    ax.tick_params(labelsize=labelsize) 
    labels = ax.get_xticklabels() + ax.get_yticklabels()
    [label.set_fontname('Times New Roman') for label in labels]
    if save == 1:
        plt.savefig(filename+file_format, dpi=dpi) 
    if show == 1:
        plt.show()
    plt.close('all')

if __name__ == '__main__':
    main()

运算结果：

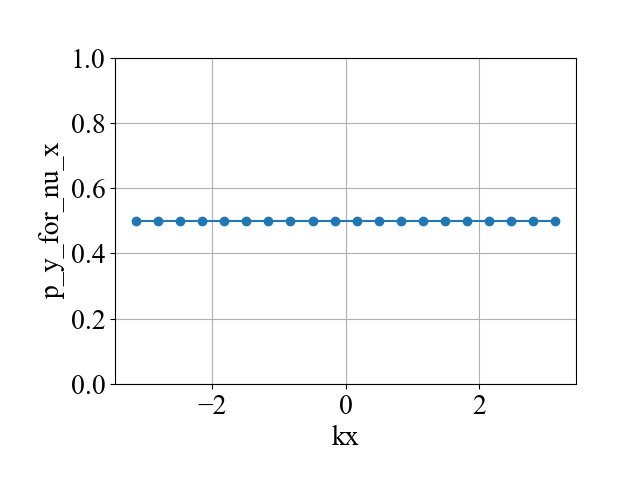
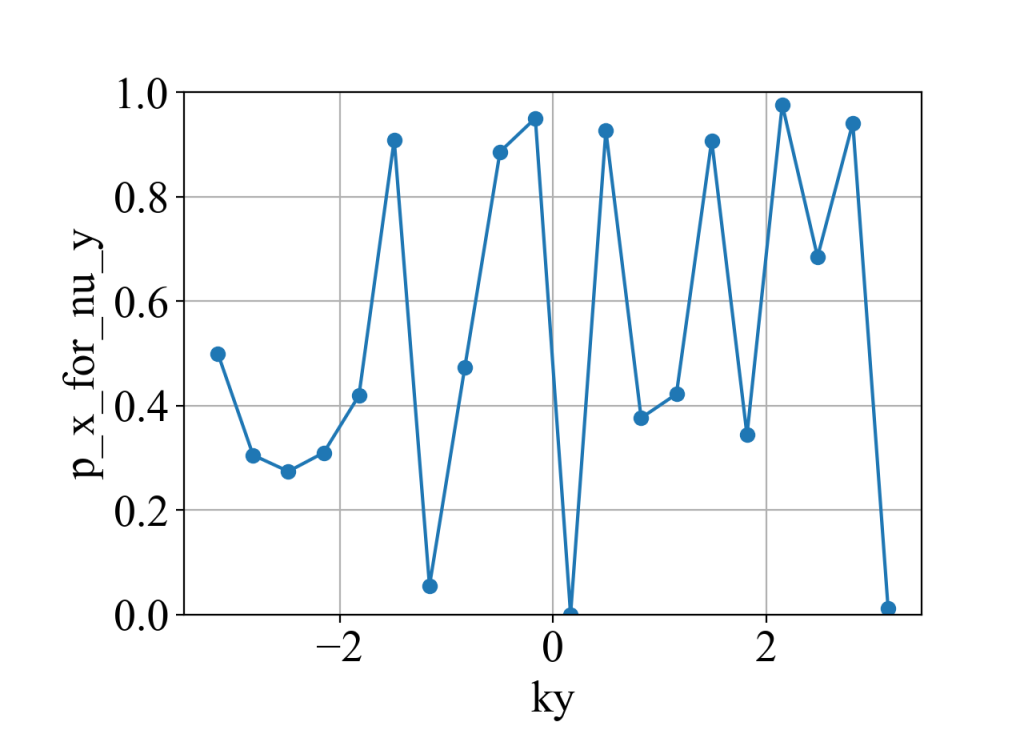
说明：

（1）代码中有些是对本征值做了重复计算，但为了代码直观就不做过多的优化。

（2）这里为了打开简并，打破了x方向的镜面对称性（ x_symmetry_breaking_2 = 0.0000000000001 ），所以p_x_for_nu_y（ $p_{x}^{v_{y}^{\pm}}$ ）没法保证是量子化。而由于y方向的镜面对称仍然保留，因此p_y_for_nu_y （ $p_{y}^{v_{x}^{\pm}}$ ）是量子化的，即[2]：

$p_{y}^{v_{x}^{\pm}}\overset{M_{y}}{=}0\ \mathrm{or} \ 1/2 \ \mathrm{mod} \ 1.$

（3）以下的代码是处理能带简并时最简单情况，只做个波函数对调，仅做参考：

if kx == -pi:
    vector1_array.append(eigenvector[:, 0])
    vector2_array.append(eigenvector[:, 1])
elif kx != pi:
    # 这里的判断是为了处理能带简并时最简单情况，只做个顺序对调。如果只是顺序反了，内积接近0。但实际会更复杂，不只是顺序的问题，而且任意的线性组合。
    if np.abs(np.dot(vector1_array[-1].transpose().conj(), eigenvector[:, 0]))>0.5:
        vector1_array.append(eigenvector[:, 0])
        vector2_array.append(eigenvector[:, 1])
    else:
        vector1_array.append(eigenvector[:, 1])
        vector2_array.append(eigenvector[:, 0])
else:
    # 这里是为了-pi和pi有相同的波函数，使得Wilson loop的值与波函数规范无关。
    vector1_array.append(vector1_array[0])
    vector2_array.append(vector2_array[0])

（4）对于简并的情况，能带波函数可能需要旋转/幺正变换，得到固定的一个波函数基[3]。在这篇“非简并波函数和简并波函数的固定规范”中，给出了具体的代码。但用上这个固定规范后似乎也不能给出正确的结果，暂时还不知道怎么处理，暂且搁置了。

参考资料：

[1] Benalcazar et al., Quantized electric multipole insulators, science 357, 6346 (2017).

[2] Benalcazar et al., Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators, Phys. Rev. B 96, 245115 (2017).

[3] S. Franca et al., An anomalous higher-order topological insulator, Phys. Rev. B 98, 201114(R) (2018). 以及补充材料

[4] 和YZZ同学的讨论

3,481 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】

Published by guanjihuan

View all posts by guanjihuan

43 thoughts on “BBH模型的nested Wilson loop高阶不变量（附Python代码）”

匿名说道：

2023年7月20日 21:47

作者您好，我想请问下这里最后说的：打破了x方向的镜面对称性，所以p_x_for_nu_y（p_{x}^{v_{y}^{\pm}}）没法保证是量子化。而由于y方向的镜面对称仍然保留，因此p_y_for_nu_y （p_{y}^{v_{x}^{\pm}}）是量子化的。
但是如果两个方向的镜面对称性都不破坏，为什么两个极化都不是量子化的呢？如果按照分析的话，应该p_x_for_nu_y和p_y_for_nu_y 两个都应该是量子化的，但是画图来看又不是？

回复
1. guanjihuan说道：
  
  2023年7月21日 00:41
  
  如果两个方向的镜面对称性都不破坏，结果应该是量子化的。这里算的之所以没有量子化，是因为这时候能带存在简并，波函数不好区分处理，所以这时候数值计算结果是错误的。我暂时还不清楚怎么处理这个简并问题，这边只是算了下非简并的情况，所以要打破一些对称性。
  
  回复
  1. 匿名说道：
    
    2023年7月21日 09:34
    
    哦哦哦好的感谢答主～
    
    回复
匿名说道：

2023年7月17日 11:09

作者您好，请问一下，在一个正方形系统中，如果仅有两个角存在简并的角态，是否可以用nested wilson loop方法表征拓扑不变量

回复
1. guanjihuan说道：
  
  2023年7月17日 11:13
  
  这个我不清楚，可以试着算下，看是否存在这个不变量。或者可能有新的拓扑不变量。
  
  回复
  1. 匿名说道：
    
    2023年8月9日 09:56
    
    谢谢回复~
    
    回复
匿名说道：

2023年5月6日 19:57

关老师，如果是6*6的矩阵，占据态的数目为3，在求解嵌套的wilson loop时，此时占据态波函数数目取1吗？

回复
1. guanjihuan说道：
  
  2023年5月7日 01:15
  
  看得到的nu_x或nu_y中价带占据态有几个吧，可能是1，也可能是2，取决于多出的一条带在哪个位置，以及自己想要考虑什么样的问题。
  
  回复
  1. 匿名说道：
    
    2023年5月8日 10:18
    
    谢谢回复
    
    回复
匿名说道：

2022年9月26日 01:12

博主你好
你这个代码跟高阶拓扑的edge polarization是等价的么？

回复
1. guanjihuan说道：
  
  2022年9月26日 16:32
  
  嗯，边界极化的量子化对应的就是高阶拓扑不变量
  
  回复
  1. 匿名说道：
    
    2022年10月1日 22:00
    
    你这里可以计算实空间的 edge polarization 么？也就是说横坐标是 X 方向的格点数。
    
    回复
    1. guanjihuan说道：
      
      2022年10月2日 02:19
      
      这里没有算。是指态密度分布吗？
      
      回复
      1. 匿名说道：
        
        2022年10月2日 12:49
        
        指的是参考资料(1)中，图2的D图
        
        回复
        
        guanjihuan说道：
        
        2022年10月3日 04:57
        
        嗯，我暂时没考虑。可以找对应的公式算。
        
        回复
匿名说道：

2022年9月17日 23:28

你好，请问可以利用这种方法计算高阶拓扑半金属中Weyl点的拓扑荷数吗，其思路是否类似？

回复
1. guanjihuan说道：
  
  2022年9月18日 16:21
  
  看定义和公式是否一样了。如果只考虑某个动量截面的高阶拓扑不变量，计算应该是类似的。参考这篇文章以及其补充材料：Higher-Order Weyl Semimetals。
  
  回复
  1. 匿名说道：
    
    2022年9月18日 16:56
    
    好的，谢谢您的回答。
    
    回复
匿名说道：

2022年9月7日 20:52

关老师您好，我最近在研究拓扑绝缘体的极化时遇到一些问题，想请假一下您。就是对于某些二维模型，比如二维SSH模型，其边界态可以由对应方向的极化来解释，但是如果把边界取成正方形对角线方向，依然有局域的边界态，但沿着新的边界方向并没有之前的极化；再比如BBH四极矩模型，沿着对角线方向取边界也会有局域态，但沿着新边界（虽然我不确定能不能这么算）算nested Wilson loops对应的极化也消失了。但是模型bulk的性质并没发生改变。所以对于新边界上的边界态似乎没有对应的极化可以描述，是否有别的方法能解释这些特殊边界态呢？

回复
1. guanjihuan说道：
  
  2022年9月8日 10:14
  
  我不确定你算的对不对。如果考虑斜对角，布里渊其还是原来的形状，所以在求nested Wilson loops的时候要注意k的范围。
  
  回复
  1. 匿名说道：
    
    2022年9月8日 10:56
    
    嗯我知道布里渊区是之前的形状，但毕竟我想求对角线方向上的nested Wilson loops的极化，所以我把布里渊区分割拼接成一个斜的长方形（宽1/sqrt(2)，长2/sqrt(2)），然后对角线方向就和长方形的长宽对应了，之后我再算nested Wilson loops的极化，就消失了，但边界态还在。您觉得我这样处理有问题吗
    
    回复
    1. guanjihuan说道：
      
      2022年9月8日 12:12
      
      我觉得可能没什么问题，计算结果好像也是正常的，因为这样算的极化对应的“角态”在物理上就不是原来那个位置，所以没有量子化。拓扑平庸的边界态很常见，不代表什么。
      
      回复
      1. 匿名说道：
        
        2022年9月8日 12:47
        
        好的，谢谢关老师
        
        回复
匿名说道：

2022年8月10日 08:38

关老师,这个嵌套威尔逊环的代码解决了以前波函数的问题吗？

回复
1. guanjihuan说道：
  
  2022年8月10日 12:40
  
  简并问题还没解决。目前暂时没做这方面的，之后如果解决了会更新。
  
  回复
匿名说道：

2022年8月5日 20:55

作者您可以了解一下实空间中体四极矩qxy拓扑不变量,和嵌套威尔逊环等价，但某些情况下更鲁棒性
DOI: 10.1103/PhysRevLett.125.166801
DOI: 10.1103/PhysRevB.101.195309

回复
1. guanjihuan说道：
  
  2022年8月6日 15:08
  
  嗯，感谢告知和提供的文献。我之前有大概了解一些，但事情比较多就暂且搁置了，之后有空再考虑考虑。这个链接有提供了相关的代码，但我还不确定是不是对的，供参考：https://github.com/kabume/Qc_real_space_method。
  
  回复
  1. 匿名说道：
    
    2022年8月6日 16:56
    
    嗯嗯，非常感谢关老师
    
    回复
    1. 匿名说道：
      
      2022年8月10日 08:37
      
      套其他玩具模型验证过了，GitHub代码的算体四极矩的思想是正确的
      
      回复
      1. 匿名说道：
        
        2023年3月31日 12:18
        
        能否请教下代码里的求Qxy好像没有像文章公式里乘根号下对角酉矩阵Q。这是为什么呢
        
        回复
        
        guanjihuan说道：
        
        2023年3月31日 18:47
        
        这个是实空间的算法吧
        
        回复
        
        匿名说道：
        
        2023年4月17日 09:10
        
        哪个文章？可以加我QQ：2437082289讨论
        
        回复
Hanliu说道：

2022年6月26日 22:24

关老师，我想请教一下，算完wilson矩阵的本征后不是已经算是得出wannier了吗？为什么还要加入下面这段代码呢？
for i0 in range(2):
if np.real(nu_x[i0]) < 0:
nu_x[i0] += 1
nu_x = np.sort(nu_x)
nu_x_array.append(nu_x.real)

回复
1. guanjihuan说道：
  
  2022年6月27日 00:23
  
  本征值有一个负值，由于在定义上只关心mod 1后的量，所以可以把负数改为正数。后面是对本征值进行排序，方便画图用的，不然连线会来回跳跃。
  
  回复
  1. 匿名说道：
    
    2022年6月27日 14:46
    
    非常感谢！
    
    回复
匿名说道：

2022年5月4日 21:12

这个能否有个Matlab程序

回复
1. guanjihuan说道：
  
  2022年5月5日 10:48
  
  目前没有的。可以直接根据定义公式来写
  
  回复
aaa说道：

2022年4月27日 23:37

你好，请问对于非四方布里渊区的体系，比如kagome晶格的六边形布里渊区，在计算Wilson loop的时候如何确定loop的方向？

回复
1. guanjihuan说道：
  
  2022年4月28日 09:33
  看你要研究什么问题了，一般来说只要是闭合的曲线都能定义Wilson loop。这个我也不了解，还没怎么考虑，你可以查下文献，例如这两篇：
  
  Disconnected elementary band representations, fragile topology, and Wilson loops as topological indices: An example on the triangular lattice
  
  Quantization of fractional corner charge in Cn-symmetric higher-order topological crystalline insulators
  回复
parkman说道：

2022年4月18日 14:40

Hi, 我加你微信了再次通过您的代码学习了很多
简并情况我尝试了一下通过简并微扰论貌似可以区分这写简并态
结果我发您邮箱吧有空我们可以讨论讨论

回复
1. 匿名说道：
  
  2024年3月21日 16:25
  
  兄弟你的简并问题解决了吗？可以加个联系方式吗？qq:2437082289
  
  回复
LC说道：

2021年12月30日 11:44

威尔逊环怎么看呢？或者怎么判断体系的拓扑性质呢？怎么预测角态边界态呢？

回复
1. guanjihuan说道：
  
  2021年12月30日 13:33
  
  看下参考文献。计算对应的高阶拓扑不变量可以预测该拓扑性质，如果高阶拓扑不变量不为零，则存在量子化的角态。
  
  回复

一、能带

二、Wilson loop

三、nested Wilson loop

Published by guanjihuan

43 thoughts on “BBH模型的nested Wilson loop高阶不变量（附Python代码）”

发表评论 取消回复

发表评论取消回复