采样的一个简单应用见这篇博文:使用蒙特卡洛计算定积分(附Python代码)。
一般的简单分布采样有:均匀分布、高斯分布、Gamma分布等,是可以直接生成得到样品的。但是对于比较复杂的分布,即使已知该分布,也很难直接获取符合该分布的样本,这时候需要使用“接受-拒绝采样”、“马尔科夫链-蒙特卡洛 (MCMC) 采样”、“ Metropolis-Hastings (M-H)采样”、“Gibbs采样”等方法。
以下是Metropolis采样的步骤,该截图来自于参考资料[5]:

如果是 Metropolis-Hastings Methods,则接受率![]() 多乘积了一项:
多乘积了一项:
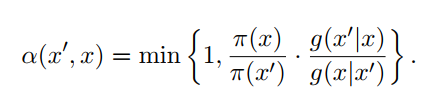
当![]() 时,就回到了Metropolis的方法。
时,就回到了Metropolis的方法。
这里介绍给出一个Metropolis采样的例子,代码如下:
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/1247
"""
import random
import math
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
def function(x): # 期望样品的分布,target distribution function
y = (norm.pdf(x, loc=2, scale=1)+norm.pdf(x, loc=-5, scale=1.5))/2 # loc代表了均值,scale代表标准差
return y
T = 100000 # 取T个样品
pi = [0 for i in range(T)] # 任意选定一个马尔科夫链初始状态
for t in np.arange(1, T):
pi_star = np.random.uniform(-10, 10) # a proposed distribution, 例如是均匀分布的,或者是一个依赖pi[t - 1]的分布
alpha = min(1, (function(pi_star) / function(pi[t - 1]))) # 接收率
u = random.uniform(0, 1)
if u < alpha:
pi[t] = pi_star # 以alpha的概率接收转移
else:
pi[t] = pi[t - 1] # 不接收转移
pi = np.array(pi) # 转成numpy格式
print(pi.shape) # 查看抽样样品的维度
plt.plot(pi, function(pi), '*') # 画出抽样样品期望的分布 # 或用plt.scatter(pi, function(pi))
plt.hist(pi, bins=100, density=1, facecolor='red', alpha=0.7) # 画出抽样样品的分布 # bins是分布柱子的个数,density是归一化,后面两个参数是管颜色的
plt.show()计算结果如下(蓝色是期望得到样品的理想分布函数,红色是采样样品的实际分布,两者是一致的):
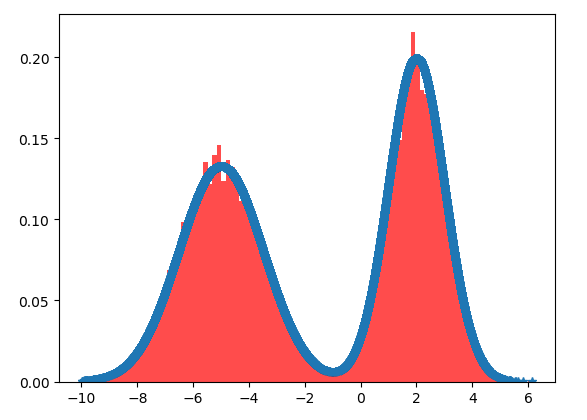
matlab代码的例子:
% This code is supported by the website: https://www.guanjihuan.com
% The newest version of this code is on the web page: https://www.guanjihuan.com/archives/1247
clc;clear all;clf;
s=100000; % 取的样品数
f=[1,2,3,3,3,3,6,5,4,3,2,1]; % 期望得到样品的分布函数
d=zeros(1,s); % 初始状态
x=1;
for i=1:s
y=unidrnd(12); % 1到12随机整数
alpha=min(1,f(y)/f(x)); % 接收率
u=rand;
if u<alpha % 以alpha的概率接收转移
x=y;
end
d(i)=x;
end
hist(d,1:1:12);计算结果:
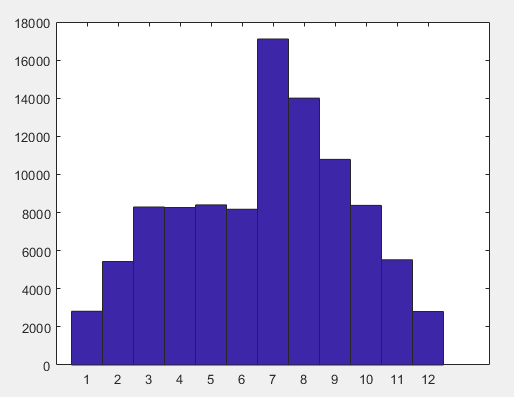
参考资料:
[2] 博文:随机采样方法(接受-拒绝采样,MCMC蒙特卡洛采样、Gibbs采样)
[3] 博文:随机采样方法整理与讲解(MCMC、Gibbs Sampling等)
[4] https://stephens999.github.io/fiveMinuteStats/MH_intro.html
[5] https://www2.stat.duke.edu/~km68/materials/214.7%20(MH).pdf
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】