六角格子的佩尔斯替换和石墨烯条带的Hofstadter蝴蝶（附Python代码）

Peierls substitution[1]：

选取磁场为方向，在朗道规范[2]下，磁势可以选为,，于是有

六角格子示意图：

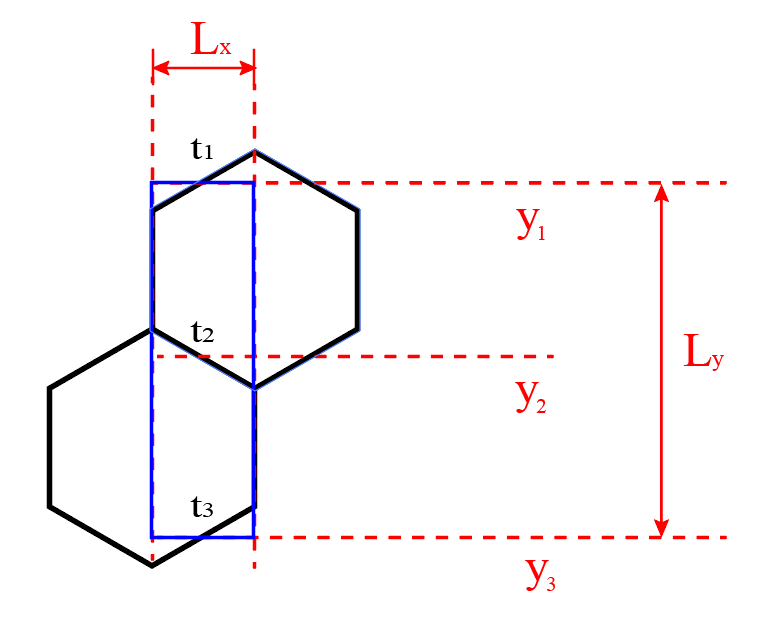
考虑以下三个跃迁：

变换得到：

假设这里的还未定义，为任意值。

令时，体系第一次进入到Hofstadter蝴蝶的循环状态。那么和都应该取整数，即和都是的整数倍。的最大值为，这时所对应的磁场是最小的，为第一次进入循环。

也就是说如果某个元胞的某个跃迁的相位是零，那么在下一个元胞的相同的位置相位应该为2pi，这样整体体系才会完全重复。

为六角格子的面积，即元胞面积。

如果格子更加复杂，例如Kagome格子[3,4]，需要考虑每个跃迁进入周期的情况，从而确定的值，最终得到的是格子最小的封闭面积。

附：有限宽度石墨烯条带的Hofstadter蝴蝶Python代码

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/12185
"""

import numpy as np
from math import *  
import cmath  
import functools 

def hamiltonian(B, k, N, M, t1, a):  # graphene哈密顿量（N是条带的宽度参数）
    # 初始化为零矩阵
    h00 = np.zeros((4*N, 4*N), dtype=complex)
    h01 = np.zeros((4*N, 4*N), dtype=complex)
    # 原胞内的跃迁h00
    for i in range(N):
        h00[i*4+0, i*4+0] = M
        h00[i*4+1, i*4+1] = -M
        h00[i*4+2, i*4+2] = M
        h00[i*4+3, i*4+3] = -M
        # 最近邻
        h00[i*4+0, i*4+1] = t1*cmath.exp(-2*pi*1j*B*(3*a*i+1/4*a)*(np.sqrt(3)/2*a))
        h00[i*4+1, i*4+0] = np.conj(h00[i*4+0, i*4+1])
        h00[i*4+1, i*4+2] = t1
        h00[i*4+2, i*4+1] = np.conj(h00[i*4+1, i*4+2])
        h00[i*4+2, i*4+3] = t1*cmath.exp(2*pi*1j*B*(3*a*i+7/4*a)*(np.sqrt(3)/2)*a)
        h00[i*4+3, i*4+2] = np.conj(h00[i*4+2, i*4+3])
    for i in range(N-1):
        # 最近邻
        h00[i*4+3, (i+1)*4+0] = t1
        h00[(i+1)*4+0, i*4+3] = t1
    # 原胞间的跃迁h01
    for i in range(N):
        # 最近邻
        h01[i*4+1, i*4+0] = t1*cmath.exp(-2*pi*1j*B*(3*a*i+1/4*a)*(np.sqrt(3)/2*a))
        h01[i*4+2, i*4+3] = t1*cmath.exp(-2*pi*1j*B*(3*a*i+7/4*a)*(np.sqrt(3)/2*a))
    matrix = h00 + h01*cmath.exp(1j*k) + h01.transpose().conj()*cmath.exp(-1j*k)
    return matrix

def main():
    N = 30
    a = 1
    hamiltonian_function0 = functools.partial(hamiltonian, k=0, N=N, M=0, t1=1, a=a)
    B_array = np.linspace(0, 1/(3*np.sqrt(3)/2*a*a), 100)
    BS_array = B_array*(3*np.sqrt(3)/2*a*a)
    eigenvalue_array = calculate_eigenvalue_with_one_parameter(B_array, hamiltonian_function0)
    plot(BS_array, eigenvalue_array, xlabel='Flux (BS/phi_0)', ylabel='E', title='Ny=%i'%N, filename='a', show=1, save=0, style='k.', y_min=None, y_max=None, markersize=3)
    
    # import guan
    # eigenvalue_array = guan.calculate_eigenvalue_with_one_parameter(B_array, hamiltonian_function0)
    # guan.plot(BS_array, eigenvalue_array, xlabel='Flux (BS/phi_0)', ylabel='E', title='Ny=%i'%N, filename='a', show=1, save=0, style='k.', y_min=None, y_max=None, markersize=3)

def calculate_eigenvalue_with_one_parameter(x_array, hamiltonian_function, print_show=0):
    dim_x = np.array(x_array).shape[0]
    i0 = 0
    if np.array(hamiltonian_function(0)).shape==():
        eigenvalue_array = np.zeros((dim_x, 1))
        for x0 in x_array:
            hamiltonian = hamiltonian_function(x0)
            eigenvalue_array[i0, 0] = np.real(hamiltonian)
            i0 += 1
    else:
        dim = np.array(hamiltonian_function(0)).shape[0]
        eigenvalue_array = np.zeros((dim_x, dim))
        for x0 in x_array:
            if print_show==1:
                print(x0)
            hamiltonian = hamiltonian_function(x0)
            eigenvalue, eigenvector = np.linalg.eigh(hamiltonian)
            eigenvalue_array[i0, :] = eigenvalue
            i0 += 1
    return eigenvalue_array

def plot(x_array, y_array, xlabel='x', ylabel='y', title='', fontsize=20, labelsize=20, show=1, save=0, filename='a', file_format='.jpg', dpi=300, style='', y_min=None, y_max=None, linewidth=None, markersize=None, adjust_bottom=0.2, adjust_left=0.2): 
    import matplotlib.pyplot as plt
    fig, ax = plt.subplots()
    plt.subplots_adjust(bottom=adjust_bottom, left=adjust_left) 
    ax.plot(x_array, y_array, style, linewidth=linewidth, markersize=markersize)
    ax.grid()
    ax.set_title(title, fontsize=fontsize, fontfamily='Times New Roman')
    ax.set_xlabel(xlabel, fontsize=fontsize, fontfamily='Times New Roman') 
    ax.set_ylabel(ylabel, fontsize=fontsize, fontfamily='Times New Roman') 
    if y_min!=None or y_max!=None:
        if y_min==None:
            y_min=min(y_array)
        if y_max==None:
            y_max=max(y_array)
        ax.set_ylim(y_min, y_max)
    ax.tick_params(labelsize=labelsize) 
    labels = ax.get_xticklabels() + ax.get_yticklabels()
    [label.set_fontname('Times New Roman') for label in labels]
    if save == 1:
        plt.savefig(filename+file_format, dpi=dpi) 
    if show == 1:
        plt.show()
    plt.close('all')

if __name__ == '__main__':
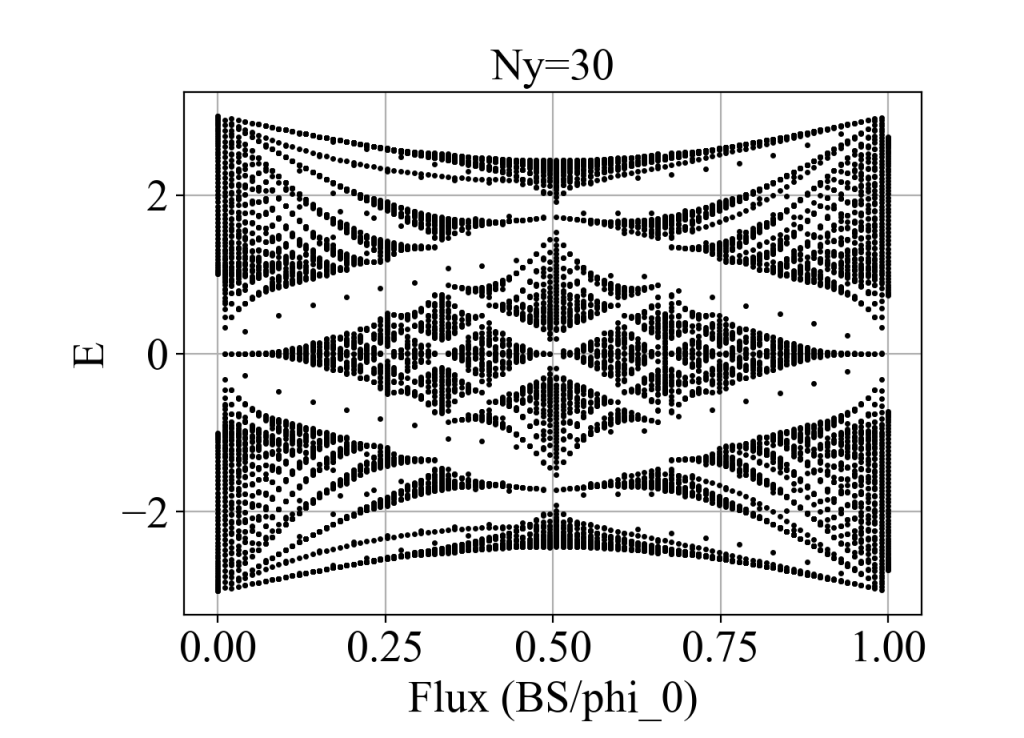
    main()

运行结果：

参考资料：

[1] 佩尔斯替换 Peierls substitution

[2] 磁场和磁势的选取

[3] Du et al. - 2018 - Floquet Hofstadter butterfly on the kagome and triangular lattices

[4] Zhang and Tong - 2019 - Staggered potential and magnetic field tunable electronic switch in a kagome nanoribbon junction

4,146 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】