参考之前的博文:二维电子气的朗道能级。
狄拉克电子最小哈密顿量:
![]()
磁场沿着![]() 方向,选取朗道规范(Landau gauge):
方向,选取朗道规范(Landau gauge):
![]()
加磁场后,薛定谔方程写为:
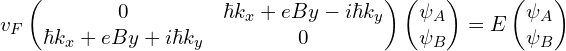
当![]() 时:
时:
![]()
![]()
其中,算符:
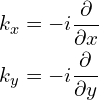
此外,波函数可以写为:
![]()
代入薛定谔方程,得到:
![]()
![]()
![]()
为了得到标准谐振子方程:
![]()
变量替换:
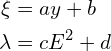
代入,得到:
![]()
![]()
通过观察,参数选为:
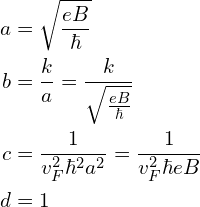
即变量替换为:
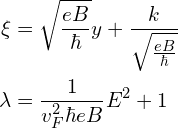
标准谐振子方程的解为:![]() ,即
,即![]()
波函数用厄密多项式表示,这里略。
前面考虑的是![]() 的情况。当
的情况。当![]() 时,代入原方程,仍然是方程的解,波函数要单独推导。
时,代入原方程,仍然是方程的解,波函数要单独推导。
此外,朗道能级还可以用粒子数算符来求解:用粒子数算符求解朗道能级。
参考资料:
[1] 广州大学Prof. Yanyang Zhang课堂笔记
[2] J. W. McClure, Diamagnetism of Graphite, Phys. Rev. 104, 666 (1956).
[3] Nguyen Hong Shon, and Tsuneya Ando, Quantum Transport in Two-Dimensional Graphite System, J. Phys. Soc. Jpn. 67, pp. 2421-2429 (1998).
[4] Li, G., Andrei, E. Observation of Landau levels of Dirac fermions in graphite. Nature Phys 3, 623–627 (2007).
[5] Yan-Yang Zhang et al, Three-dimensional topological insulator in a magnetic field: chiral side surface states and quantized Hall conductance, J. Phys.: Condens. Matter 24 015004 (2012).
[6] Yin, LJ., Bai, KK., Wang, WX. et al. Landau quantization of Dirac fermions in graphene and its multilayers. Front. Phys. 12, 127208 (2017).
[7] A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov, and A. K. Geim, The electronic properties of graphene, Rev. Mod. Phys. 81, 109 (2009).
[8] http://web.physics.ucsb.edu/~phys123B/w2015/lecture5.pdf
[9] 季燕江《量子力学讲义》的4.2节、6.5节、8.3节
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】
老师,您这里如果解的是Ψ_B的话好像就会出现没有零能级的情况,这该怎么解释呢?
我也不大清楚。应该不会不一样吧,好像是对称的。
老师您好,我想请问一下狄拉克电子的最小哈密顿量是怎么写出来的呢?在哪些课本上有这方面的知识点吗?
其实形式不是唯一的,只要本征值是线性的就可以。只是用泡利矩阵来写,这样是最简洁和直接的。
参考:
[1] 由泡利矩阵组成的哈密顿量的本征值
[2] 石墨烯紧束缚模型到低能有效模型的推导
老师您好,我想问一下推导过程中,当E≠0时,第二条式子中为什么掉了一项eBy·ihk_y呢?
用到位置和动量的对易关系。
明白了,谢谢老师