拓扑不变量, 学术

SSH模型中的Wilson loop（附Python代码）

发布时间：

最近修改时间：2024年1月25日

这是之前的一篇关于SSH模型的博文：SSH模型的哈密顿量、能带图和卷绕数（附Python代码）。除了卷绕数（winding number）这个不变量，我们还可以计算Wilson loop，进而得到电极化（polarization），或称为电偶极矩（dipole moment）。本篇内容主要来源于文献[1]。

这里写出SSH模型哈密顿量：

h(k)=\begin{pmatrix}0 & \gamma+\lambda e^{-ik} \\\gamma+\lambda e^{ik} & 0\end{pmatrix}

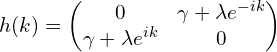
该哈密顿量满足空间反演对称性（inversion symmetry）：

\hat{\mathcal{I}}h(k)\hat{\mathcal{I}}^{-1}=h(-k)

其中，空间反演对称性算符为\hat{\mathcal{I}}=\sigma_1。

同时也满足手征对称性（chiral symmetry）：

\hat{\Pi}h(k)\hat{\Pi}^{-1}=-h(k)

其中，手征对称性算符为\hat{\Pi}=\sigma_3。

可证明：在空间反演对称性或手征对称性下，偶极矩均可量子化到0或者\frac{1}{2}（mod 1）。证明见参考资料[1]。

SSH模型同时满足以上这两种对称性，因此偶极矩是量子化的。当|\gamma|>|\lambda|时，极化p=0；当|\gamma|<|\lambda|时，极化p=\frac{1}{2}。

如果在SSH模型的哈密顿量中加入\sigma_3项，会同时打破模型的空间反演对称性和手征对称性，这时候偶极矩不再量子化。

说明：这里添加了固定波函数规范的代码，在本篇博文后面给出了更好的代码，不需要对波函数进行规范。固定规范的方法介绍也可参考这篇：非简并波函数和简并波函数的固定规范。

一、当|\gamma|<|\lambda|时，代码如下：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/10064
"""

import numpy as np
import cmath
from math import *

def hamiltonian(k):  # SSH模型哈密顿量
    gamma = 0.5
    lambda0 = 1
    h = np.zeros((2, 2), dtype=complex)
    h[0,0] = 0
    h[1,1] = 0
    h[0,1] = gamma+lambda0*cmath.exp(-1j*k)
    h[1,0] = gamma+lambda0*cmath.exp(1j*k)
    return h

def main():
    Num_k = 100
    k_array = np.linspace(-pi, pi, Num_k)
    vector_array = []
    for k in k_array:
        vector  = get_occupied_bands_vectors(k, hamiltonian)   
        # vector_array.append(vector)
        vector_array.append(vector*cmath.exp(1j*np.random.uniform(0, pi))) # 随机相位测试

    # 波函数固定一个规范
    vector_sum = 0
    for i0 in range(Num_k):
        vector_sum += np.abs(vector_array[i0])
    index = np.argmax(np.abs(vector_sum))
    for i0 in range(Num_k):
        angle = cmath.phase(vector_array[i0][index])
        vector_array[i0] = vector_array[i0]*cmath.exp(-1j*angle)
        # vector_array[i0] = find_vector_with_fixed_gauge_by_making_one_component_real(vector_array[i0], index=index) # 或者使用这种寻找查找方法，计算效率比较低

    # 计算Wilson loop
    W_k = 1
    for i0 in range(Num_k-1):
        F = np.dot(vector_array[i0+1].transpose().conj(), vector_array[i0])
        W_k = np.dot(F, W_k)
    nu = np.log(W_k)/2/pi/1j
    # if np.real(nu) < 0:
    #     nu += 1
    print('p=', nu)
    
def get_occupied_bands_vectors(x, matrix):  
    matrix0 = matrix(x)
    eigenvalue, eigenvector = np.linalg.eig(matrix0) 
    vector = eigenvector[:, np.argsort(np.real(eigenvalue))[0]] 
    return vector

# def find_vector_with_fixed_gauge_by_making_one_component_real(vector, precision=0.005, index=None):
#     if index == None:
#         index = np.argmax(np.abs(vector))
#     sign_pre = np.sign(np.imag(vector[index]))
#     for phase in np.arange(0, 2*np.pi, precision):
#         sign =  np.sign(np.imag(vector[index]*cmath.exp(1j*phase)))
#         if np.abs(np.imag(vector[index]*cmath.exp(1j*phase))) < 1e-9 or sign == -sign_pre:
#             break
#         sign_pre = sign
#     vector = vector*cmath.exp(1j*phase)
#     if np.real(vector[index]) < 0:
#         vector = -vector
#     return vector

if __name__ == '__main__':
    main()

计算结果为：

p= (-0.5+0.009257772639491353j)

二、当|\gamma|<|\lambda|时：

def hamiltonian(k):  # SSH模型哈密顿量
    gamma = 1.5
    lambda0 = 1
    h = np.zeros((2, 2), dtype=complex)
    h[0,0] = 0
    h[1,1] = 0
    h[0,1] = gamma+lambda0*cmath.exp(-1j*k)
    h[1,0] = gamma+lambda0*cmath.exp(1j*k)
    return h

计算结果为：

p= (-6.308806949364591e-17+0.003169518547424918j)

三、在SSH模型的哈密顿量中加入\sigma_3项：

def hamiltonian(k):
    gamma = 0.5
    lambda0 = 1
    delta = 0.3
    h = np.zeros((2, 2), dtype=complex)
    h[0,0] = delta
    h[1,1] = -delta
    h[0,1] = gamma+lambda0*cmath.exp(-1j*k)
    h[1,0] = gamma+lambda0*cmath.exp(1j*k)
    return h

计算结果为：

p= (0.328981519117191+0.007898978069732571j)

由评论区Kabu Xiong提供的资料[5]，指出了Wilson loop对相位是不依赖的，是gauge invariant，这是因为在Wilson loop 中，波函数都出现了两次，而且是相互复数共轭，相位刚好相消。

然而在程序中，我们把vector_array.append(vector)修改成vector_array.append(vector*cmath.exp(1j*np.random.uniform(0, pi)))，也就是每个波函数加一个随机的相位。这时候只有加了波函数规范的代码，结果才是正确的。

原因在于-pi和pi两个点的波函数应该是要相位相同。如果两个点是独立算的，那么相位是不能完全相消的。因此，如果在程序中不重新算pi点的波函数，直接引用-pi点的波函数，这时候是不需要对波函数进行规范。

代码如下（建议采用这种更好方式）：

"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/10064
"""

import numpy as np
import cmath
from math import *


def hamiltonian(k):
    gamma = 0.5
    lambda0 = 1
    delta = 0
    h = np.zeros((2, 2), dtype=complex)
    h[0,0] = delta
    h[1,1] = -delta
    h[0,1] = gamma+lambda0*cmath.exp(-1j*k)
    h[1,0] = gamma+lambda0*cmath.exp(1j*k)
    return h


def main():
    Num_k = 100
    k_array = np.linspace(-pi, pi, Num_k)
    vector_array = []
    for k in k_array:
        vector  = get_occupied_bands_vectors(k, hamiltonian)   
        if k != pi:
            vector_array.append(vector)
        else:
            vector_array.append(vector_array[0])

    # 计算Wilson loop
    W_k = 1
    for i0 in range(Num_k-1):
        F = np.dot(vector_array[i0+1].transpose().conj(), vector_array[i0])
        W_k = np.dot(F, W_k)
    nu = np.log(W_k)/2/pi/1j
    # if np.real(nu) < 0:
    #     nu += 1
    print('p=', nu, '\n')
    

def get_occupied_bands_vectors(x, matrix):  
    matrix0 = matrix(x)
    eigenvalue, eigenvector = np.linalg.eig(matrix0) 
    vector = eigenvector[:, np.argsort(np.real(eigenvalue))[0]] 
    return vector


if __name__ == '__main__':
    main()

这时，即使把vector_array.append(vector)修改成vector_array.append(vector*cmath.exp(1j*np.random.uniform(0, pi)))，也就是每个波函数加一个随机的相位，即使没有波函数规范的代码结果都是正确的。

参考资料：

[1] Wladimir A. Benalcazar, B. Andrei Bernevig, and Taylor L. Hughes， “Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators", Phys. Rev. B 96, 245115 (2017): P8-P13

[2] S. Franca, J. van den Brink, and I. C. Fulga, "An anomalous higher-order topological insulator", Phys. Rev. B 98, 201114(R) (2018).

[3] 凝聚态中的拓扑（四）：从TKNN到Z2拓扑绝缘体

[4] Band topology in classical waves: Wilson-loop approach to topological numbers and fragile topology

[5] 和YZZ同学的讨论

7,675 次浏览

【说明：本站主要是个人的一些笔记和代码分享，内容可能会不定期修改。为了使全网显示的始终是最新版本，这里的文章未经同意请勿转载。引用请注明出处：https://www.guanjihuan.com】

头像

Published by guanjihuan

48 thoughts on “SSH模型中的Wilson loop（附Python代码）”

  2. 请问，SSH模型中缠绕数和wilson loop都是拓扑不变量，它们之间有什么关系？手征对称的系统的缠绕数和wilson loop都是等价的吗？

    回复

    1. 缠绕数（winding number）通常是需要定义在手征对称的系统中， 而 Wilson loop 可以定义在任意的闭合路径上。它们不是完全等价的。

      但在具有手征对称性的系统中，它们可以传达相似的拓扑信息。我个人的理解是它们是一致的，但我没详细证明过，这篇文献 “Connection between the winding number and the Chern number [https://doi.org/10.1016/j.cjph.2020.12.025]” 有给出卷绕数和陈数的关系，我还没详细看过，供参考。另外，陈数和 poralization/Wilson loop 也是有关系的，所以对于手征对称的系统，卷绕数和 Wilson loop 有一定的对应关系。

      可能还有其他的文献中也讨论过这个问题，例如：这篇文献 “Band topology in classical waves: Wilson-loop approachto topological numbers andfragile topology [https://doi.org/10.1088/1367-2630/ab3f71]” ，以及这个讲义 “Lecture notes on Berry phases and topology [https://scipost.org/SciPostPhysLectNotes.51]”。更多文献可以自己搜一下。

      回复

      1. 谢谢！还想问一下，对于高阶拓扑绝缘体的nested wilson loop，在手征对称系统中有缠绕数这样的对应物吗？

        回复

        1. 我目前没做这个高阶拓扑的方向，不是很了解，没法解决你的问题。你可以搜些文献看看有没有这方面的研究。

          回复

  3. 老师，您好，当p= (0.328981519117191+0.007898978069732571j)，说明是平庸的吗还是非平庸，计算结果不是近似0.5或者0. 可以判断是平庸非平庸吗？是不是只要不是0 就是非平庸？

    回复

    1. 如果是非零的，但不是0.5，只能说可能有极化，但不是量子化的。这不算拓扑，属于平庸的。

      回复

  4. 关老师，为什么我用二分法找相似规范，每次都是找不到规范呢？这是代码，您能帮我看看吗？

    import guan
import numpy as np
import cmath
from math import *

def hamiltonian(kx,kw):
    kap1 = 0.6
    gam1 = 1

    kap2 = kap1
    gam2 = gam1
    d = 1
    Ome = 1
    h = np.zeros((4,4), dtype=complex)
    h[0, 1] = kap2 + gam2*cmath.exp(-1j*kx*d)
    h[0, 3] = kap1 + gam1*cmath.exp(-1j*kw*Ome)
    h[1, 0] = np.conj(h[0, 1])
    h[1, 2] = kap1 + gam1*cmath.exp(-1j*kw*Ome)
    h[2, 1] = np.conj(h[1, 2])
    h[2, 3] = kap2 + gam2*cmath.exp(1j*kx*d)
    h[3, 0] = np.conj(h[0, 3])
    h[3, 2] = np.conj(h[2, 3])
    return h


Nkx = 101
Nkw = 101
kx_array = np.linspace(-pi, pi, Nkx)
kw_array = np.linspace(-pi, pi, Nkw)
dkx = kx_array[2] - kx_array[1]
dkw = kw_array[2] - kw_array[1]
eig_value_array = np.zeros((Nkx, Nkw, 4),dtype=complex)
px0 = 0

for k0 in range(Nkx-1):
    kx = kx_array[k0]
    for j0 in range(Nkw-1):
        kw = kw_array[j0]

        eig_value, eig_vector = np.linalg.eigh(hamiltonian(kx, kw))
        vector = eig_vector[:, 0]   # (kx,kw)处的波函数
        eig_value_array[k0, j0, :] = eig_value

        eig_value, eig_vector = np.linalg.eigh(hamiltonian(kx+dkx, kw))
        vector_kx = eig_vector[:, 0]   # 略偏离kx的波函数

        rand = np.random.uniform(-pi, pi)
        vector_kx = vector_kx * cmath.exp(-1j * rand)

        vector_kx = guan.find_vector_with_the_same_gauge_with_binary_search(vector_kx, vector)


        Ax = np.dot(vector.transpose().conj(), (vector_kx-vector)/dkx)
        px0 = px0 + Ax*dkx*dkw
Px = px0/(2*pi)/(2*pi)

    回复

    1. 你算的这个波函数的本征值是简并的吧，如果有简并的情况，我目前还不知道怎么处理，因为波函数的任意线性组合都是波函数本身，而且波函数也无法根据本征值进行排序。简并的情况可以参考这篇（目前代码并不是很高效，仅供参考）：非简并波函数和简并波函数的固定规范。

      回复

  7. 感谢博主的分享，想把代码改成matlab学习编程思路。
    vector = eigenvector[:, np.argsort(np.real(eigenvalue))[0]] 这句代码的意思是要提取每次计算的特征向量吗？不明白。每次计算都会有两个特征向量。

    回复

      1. clear
        clc
        close all

        k0=linspace(-pi,pi,100);
        for i=1:100
        str=zeros(2,1);
        k=k0(i);
        h1=HH(k);
        [V,D]=eig(h1);
        vector=V(:,1); %取能量低的一条带
        if k~=pi
        VV(:,i)=vector;
        else
        VV(:,i)=V(:,1);
        end
        end
        W_k=1;
        for j=1:99
        F=dot(VV(:,j+1)',VV(:,j));
        ff(:,j)=F;
        W_k=dot(F,W_k);
        end
        nu=log(W_k)/(2*pi*1i);

        function h=HH(k)
        gamma=0.5;
        lambda0=1;
        delta=0;
        h=zeros(2);
        h(1,1)=delta;
        h(2,2)=-delta;
        h(1,2)=gamma+lambda0*exp(-1i*k);
        h(2,1)=gamma+lambda0*exp(1i*k);
        end

        结果没对，不知道是哪里出了问题
        W_k=1.32804668806497e-33 + 5.66626118539546e-49i；
        nu=6.79052539801457e-17 + 12.0482836587981i;

        回复

        1. 在matlab中，dot(A, B)已经包含了对A的厄密共轭， 即：dot(A, B)=A'*B。所以不需要额外再加一撇。

          回复

  8. 对于计算wilson loop那一块，初始化为1，然后做i0循环。 我想请问 计算下来的F是一个数还是一个矩阵，就涉及到F后面的两个波函数内积的情况，是行矢量点乘列矢量还是列矢量点乘行矢量。 后面是调用np.dot我理解上是矩阵乘法，但是初始化的是一个数。所以我想请问，F是矩阵还是数。 这个问题我可以用博主的代码自己打开看看，先在这里问一下。

    回复

  9. 老师您好，请问对于一些简并能带计算Berry Curvature的时候，需要考虑non-Abelian的Berry Curvature，从定义上虽然能做但会不会波函数的随机相位在数值上会有问题呢？这方面最近有数值方面的工作吗

    回复

    1. 简并的时候比较麻烦，如果需要波函数连续，可能是要对简并的波函数基做幺正变换。目前我还没做过测试。

      回复

  10. 博主您好，请问为什么把本征矢乘以一个，能使模最大分量变实数的一个相因子，就可以达到统一规范的目的呢？（从你的代码中看出来似乎是这个逻辑）

    回复

    1. 因为波函数乘exp(i*phase)都是方程的解，所以每一个k点的波函数计算可能存在不同的规范。把波函数某个分量变成实数，可以起到固定规范的作用，从而达到波函数连续，这是因为乘一个exp(i*phase)都会导致该分量为非实数。而至于为什么取最大分量，是为了避开波函数分量为0的情况，从而使得代码运行不容易出错。
      该方法可以参照文献“An anomalous higher-order topological insulator - An anomalous higher-order topological insulator”的补充材料中的说明。
      另外再强调下：Wilson loop的计算可以不考虑波函数的规范任意性（前提是-pi和pi的位置用同一个波函数）。

      回复

      1. 这个分量在各个波函数中也不必是同一个位置的是吧？谢谢您的回复和提供的文献，我再学习下这篇文献。

        回复

    2. 局部使得波函数最大分量变实数可能还不一定使得波函数连续，需要考虑整个布里渊区，目前代码已经完成补充修改。我猜是存在两个k点的最大分量处于不同位置的情况，尤其是临界点附近（即存在两个最大分量），所以需要全程固定一个指标（index），虽然旧代码在这个案例中没出现错误。
      但这种方案仍存在一点问题，需要小心存在局部k点该分量为0左右。即使该分量整个布里渊区是最大的，但不排除某些k点为0+或0-。对于这种情况，需要提高相位查找的精度来解决。

      回复

  11. 请问这个波函数的规范是什么含义呢？
    之前计算一个周期晶格的不变量，跟wilson loop非常像，计算过程相同，但是波函数用的是bloch函数的周期部分(即补上相位exp(ikr)以后的部分)，积分路径是k空间上的若干个小平行四边形，结果吻合得很好。中间好像没有涉及到对波函数的规范，所以不太明白规范的具体意义

    回复

    1. 不变量和可观测量都是和规范的无关的（gauge independent）。波函数相位的选取主要是在数值计算过程中会产生，例如求导时相邻的两个波函数需要连续。这里计算wilson loop也不需要选取规范，前提是把-pi和pi两个点选取为同一个波函数（这两个点本身就是同一个状态）。

      回复

    1. 如果带不相交或者简并，照样算就可以了。如果存在多个带相交或者简并，会麻烦一些，目前我还没考虑。

      回复

    1. 感谢提供的资料。Wilson loop是规范不变的。代码稍微调整下，是不需要对波函数进行规范，博文已经更新。

      回复

  15. 作者您好！我想请问一下，如何用python循环出SSH模型的实空间中的哈密顿？谢谢！

    回复

  16. 作者你好，我想问一下，“ # 波函数固定一个规范”那一步是为什么呀，我用你的代码把这一步去掉后，也能得到相同的结果。如果不规范会有什么问题吗

    回复

    1. 如果把vector_array.append(vector)修改成vector_array.append(vector*cmath.exp(1j*np.random.uniform(0, 1)))，也就是每个波函数加一个随机的相位。这时候只有加了波函数规范的代码，结果才是正确的。

      回复

      1. 哦哦，明白些了。还有一个问题，就是我想问一下那个波函数规范的公式原型是怎样的呀，我从代码上分析不出来，也没有看到相关的资料说明。谢谢！

        回复

        1. 目前没看到什么公式，只要使得波函数连续即可。可以自己写代码进行判断。

          固定一个规范的目的也是使得波函数连续。这里代码选取的规范是使波函数的最大分量（不为零的分量）的虚部为零。也可以选取其他规范。

          回复

    2. 博文更新了。因为wilson loop是gauge invariant，所以适当调整下代码，是可以不需要对波函数进行规范。

      回复

发表评论

您的邮箱地址不会被公开。 必填项已用 * 标注

Captcha Code