一、薛定谔绘景
在外场![]() 的作用下,哈密顿量
的作用下,哈密顿量![]() 随时间变化。
随时间变化。
1. 态矢量
态矢量:![]()
薛定谔方程:![]()
2. 算符
在薛定谔绘景下,规定算符![]() (除
(除![]() 外)不随时间变化,即:
外)不随时间变化,即:![]()
3. 算符平均值
算符![]() 的平均值为:
的平均值为:![]()
当该平均值为守恒量时,有:![]()
于是得到:![]()
4. 表象基矢
以![]() 作为表象,基矢为
作为表象,基矢为![]() 。
。
本征方程:![]()
正交归一:![]()
在薛定谔绘景下,态矢量随时间变化,基矢不随时间变化。
二、海森堡绘景
1. 态矢量
态矢量:![]()
当![]() 时,
时,![]()
逆关系:![]()
态矢量关系使用两次:![]()
得到![]()
在薛定谔绘景下,规定态矢量不随时间变化,即:![]()
2. 算符
算符:![]()
当![]() 时,
时,![]()
算符随时间演化:
![Rendered by QuickLaTeX.com \begin{aligned}i\hbar \frac{\partial}{\partial t}\hat{A}_H(t) &=i\hbar \frac{\partial}{\partial t}\big[\hat{U}^{\dagger}(t, t_0)\hat{A}_S(t)\hat{U}(t, t_0)\big]\\&=[\hat{A}_H(t), \hat{H}_H(t)]+i\hbar[\frac{\partial}{\partial t}\hat{A}_S(t)]_H\end{aligned}](https://www.guanjihuan.com/wp-content/ql-cache/quicklatex.com-8ad957d621b69e09ca439172d49caa33_l3.png)
其中:
![]()
![]()
算符随时间演化的方程称为海森堡方程,初始条件为:![]() 。
。
3. 算符平均值
算符![]() 的平均值为:
的平均值为:
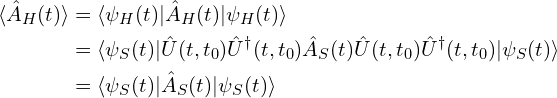
4. 表象基矢
以![]() 作为表象,基矢为
作为表象,基矢为![]() 。
。
本征方程:![]()
其中:![]()
之所以本征值是![]() ,这是因为:
,这是因为:
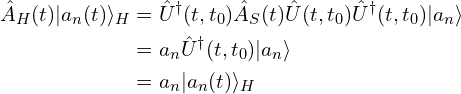
正交归一:![]()
在海森堡绘景下,态不随时间变化,基矢量随时间变化。
三、相互作用绘景
哈密顿量:![]()
1. 态矢量
态矢量:![]()
其中,![]() ,用到的未受到微扰的哈密顿量。
,用到的未受到微扰的哈密顿量。
当![]() 时,
时,![]()
态随着时间的演化:
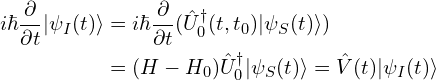
态随着时间的演化与微扰![]() 有关。
有关。
初始条件:![]()
2. 算符
算符:![]()
当![]() 时,
时,![]()
算符随时间演化:
![Rendered by QuickLaTeX.com \begin{aligned}i\hbar \frac{\partial}{\partial t}\hat{A}_I(t) &=i\hbar \frac{\partial}{\partial t}\big[\hat{U}_0^{\dagger}(t, t_0)\hat{A}_S(t)\hat{U}_0(t, t_0)\big]\\&=[\hat{A}_I(t), (\hat{H}_0(t))_I]+i\hbar[\frac{\partial}{\partial t}\hat{A}_S(t)]_I\end{aligned}](https://www.guanjihuan.com/wp-content/ql-cache/quicklatex.com-4871b5aad442d6c3cd77e28d2c3ede8e_l3.png)
其中:
![]()
![]()
算符随时间演化与未受到微扰的哈密顿量![]() 有关。
有关。
初始条件:![]()
3. 算符平均值
算符![]() 的平均值为:
的平均值为:
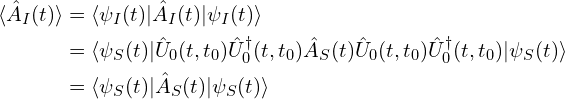
4. 表象基矢
以![]() 作为表象,基矢为
作为表象,基矢为![]() 。
。
本征方程:![]()
其中:![]()
正交归一:![]()
相互作用绘景就是在未受到微扰时的海森堡绘景。相互作用绘景又称为狄拉克绘景。在相互作用绘景下,态和基矢都随时间变化。
参考资料:
[1] 国科大金彪老师“高等量子力学”手稿课件
[2] 知乎:三种绘景
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】