BBH模型(Benalcazar-Bernevig-Hughes Model)的参考文献为:Wladimir A. Benalcazar, B. Andrei Bernevig, and Taylor L. Hughes, "Quantized electric multipole insulators", Science Volume 357:61-66 (2017).
模型:
![Rendered by QuickLaTeX.com \begin{aligned} h=&[\gamma+\lambda cos(k_x)]\Gamma_4+\lambda sin(k_x)\Gamma_3\\ &+[\gamma+\lambda cos(k_y)]\Gamma_2+\lambda sin(k_y)\Gamma_1+\delta \Gamma_0 \end{aligned}](https://www.guanjihuan.com/wp-content/ql-cache/quicklatex.com-c5c4ffbaf1712ec89f79dc1a80d68d1b_l3.png)
其中,
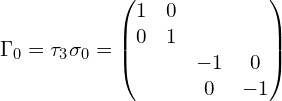
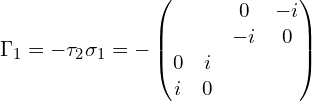
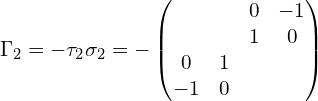
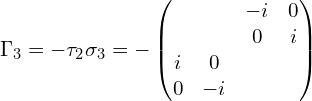
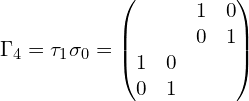
以上用到泡利矩阵的张量积:泡利矩阵以及泡利矩阵的张量积。
所以哈密顿量展开写为:
![Rendered by QuickLaTeX.com \begin{aligned}h&=\begin{pmatrix}\delta & 0 & \gamma+\lambda cos(k_x)+i\lambda sin(k_x) & \gamma+\lambda cos(k_y)+i \lambda sin(k_y) \\0 & \delta & -[\gamma+\lambda cos(k_y)]+i \lambda sin(k_y) & \gamma+\lambda cos(k_x)-i \lambda sin(k_x) \\\gamma+\lambda cos(k_x)-i \lambda sin(k_x) & -[\gamma+\lambda cos(k_y)]-i \lambda sin(k_y) & -\delta & 0 \\\gamma+\lambda cos(k_y)-i \lambda sin(k_y) & \gamma+\lambda cos(k_x)+i \lambda sin(k_x) & 0 & -\delta\end{pmatrix}\\&=\begin{pmatrix}\delta & 0 & \gamma+\lambda exp(ik_x) & \gamma+\lambda exp(ik_y) \\0 & \delta & -\gamma-\lambda exp(-i k_y) & \gamma+\lambda exp(-i k_x) \\\gamma+\lambda exp(-i k_x) & -\gamma-\lambda exp(i k_y) & -\delta & 0 \\\gamma+\lambda exp(-ik_y) & \gamma+\lambda exp(i k_x) & 0 & -\delta\end{pmatrix}\end{aligned}](https://www.guanjihuan.com/wp-content/ql-cache/quicklatex.com-11b11605827f27a5d8798a6c04221f74_l3.png)
文献中给出的对应示意图:
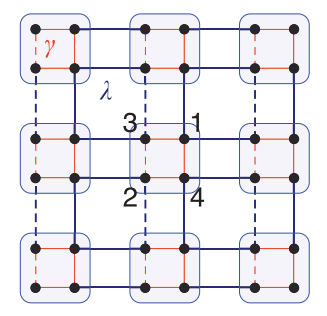
元胞为(1,2,3,4)。把哈密顿量反傅里叶变换后,可以知道:
- 元胞内部:3到1的跃迁项为
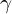 ;2到4的跃迁项为
;2到4的跃迁项为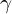 ;4到1的跃迁项为
;4到1的跃迁项为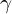 ;2到3的跃迁项为
;2到3的跃迁项为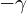 。
。 - 元胞之间:1到3的跃迁项为
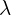 ;4到2的跃迁项为
;4到2的跃迁项为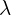 ;1到4的跃迁项为
;1到4的跃迁项为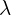 ;3到2的跃迁项为
;3到2的跃迁项为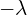 。
。
即:元胞内部跃迁项绝对值为![]() ,元胞间的跃迁项绝对值为
,元胞间的跃迁项绝对值为![]() 。此外,2和3之间的跃迁要加个负号。
。此外,2和3之间的跃迁要加个负号。
计算局域态密度(LDOS)的Python代码为:
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/8557
"""
import numpy as np
from math import *
def hamiltonian(Nx, Ny):
delta = 1e-3
gamma = 1e-3
lambda0 = 1
h = np.zeros((4*Nx*Ny, 4*Nx*Ny))
# 元胞内部跃迁
for x in range(Nx):
for y in range(Ny):
h[x*Ny*4+y*4+0, x*Ny*4+y*4+0] = delta
h[x*Ny*4+y*4+1, x*Ny*4+y*4+1] = delta
h[x*Ny*4+y*4+2, x*Ny*4+y*4+2] = -delta
h[x*Ny*4+y*4+3, x*Ny*4+y*4+3] = -delta
h[x*Ny*4+y*4+0, x*Ny*4+y*4+2] = gamma
h[x*Ny*4+y*4+0, x*Ny*4+y*4+3] = gamma
h[x*Ny*4+y*4+1, x*Ny*4+y*4+2] = -gamma
h[x*Ny*4+y*4+1, x*Ny*4+y*4+3] = gamma
h[x*Ny*4+y*4+2, x*Ny*4+y*4+0] = gamma
h[x*Ny*4+y*4+2, x*Ny*4+y*4+1] = -gamma
h[x*Ny*4+y*4+3, x*Ny*4+y*4+0] = gamma
h[x*Ny*4+y*4+3, x*Ny*4+y*4+1] = gamma
# y方向上的元胞间跃迁
for x in range(Nx):
for y in range(Ny-1):
h[x*Ny*4+y*4+0, x*Ny*4+(y+1)*4+3] = lambda0
h[x*Ny*4+(y+1)*4+1, x*Ny*4+y*4+2] = -lambda0
h[x*Ny*4+y*4+2, x*Ny*4+(y+1)*4+1] = -lambda0
h[x*Ny*4+(y+1)*4+3, x*Ny*4+y*4+0] = lambda0
# x方向上的元胞间跃迁
for x in range(Nx-1):
for y in range(Ny):
h[x*Ny*4+y*4+0, (x+1)*Ny*4+y*4+2] = lambda0
h[(x+1)*Ny*4+y*4+1, x*Ny*4+y*4+3] = lambda0
h[(x+1)*Ny*4+y*4+2, x*Ny*4+y*4+0] = lambda0
h[x*Ny*4+y*4+3, (x+1)*Ny*4+y*4+1] = lambda0
return h
def main():
Nx = 10
Ny = 10
fermi_energy = 0
h = hamiltonian(Nx, Ny)
green = np.linalg.inv((fermi_energy+1e-6j)*np.eye(h.shape[0])-h)
x_array = []
y_array = []
DOS = []
for x in range(Nx):
for y in range(Ny):
x_array.append(x*2+2)
y_array.append(y*2+2)
DOS.append(-np.imag(green[x*Ny*4+y*4+0, x*Ny*4+y*4+0])/pi)
x_array.append(x*2+1)
y_array.append(y*2+1)
DOS.append(-np.imag(green[x*Ny*4+y*4+1, x*Ny*4+y*4+1])/pi)
x_array.append(x*2+1)
y_array.append(y*2+2)
DOS.append(-np.imag(green[x*Ny*4+y*4+2, x*Ny*4+y*4+2])/pi)
x_array.append(x*2+2)
y_array.append(y*2+1)
DOS.append(-np.imag(green[x*Ny*4+y*4+3, x*Ny*4+y*4+3])/pi)
DOS = DOS/np.sum(DOS)
Plot_2D_Scatter(x_array, y_array, DOS, xlabel='x', ylabel='y', title='BBH Model', filename='BBH Model')
def Plot_2D_Scatter(x, y, value, xlabel='x', ylabel='y', title='title', filename='a'):
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
plt.subplots_adjust(bottom=0.2, right=0.8, left=0.2)
for i in range(np.array(x).shape[0]):
ax.scatter(x[i], y[i], marker='o', s=1000*value[i], c=[(1,0,0)])
ax.set_title(title, fontsize=20, fontfamily='Times New Roman')
ax.set_xlabel(xlabel, fontsize=20, fontfamily='Times New Roman')
ax.set_ylabel(ylabel, fontsize=20, fontfamily='Times New Roman')
ax.tick_params(labelsize=15) # 设置刻度值字体大小
labels = ax.get_xticklabels() + ax.get_yticklabels()
[label.set_fontname('Times New Roman') for label in labels] # 设置刻度值字体
# plt.savefig(filename+'.jpg', dpi=300)
plt.show()
plt.close('all')
if __name__ == '__main__':
main()计算结果为:
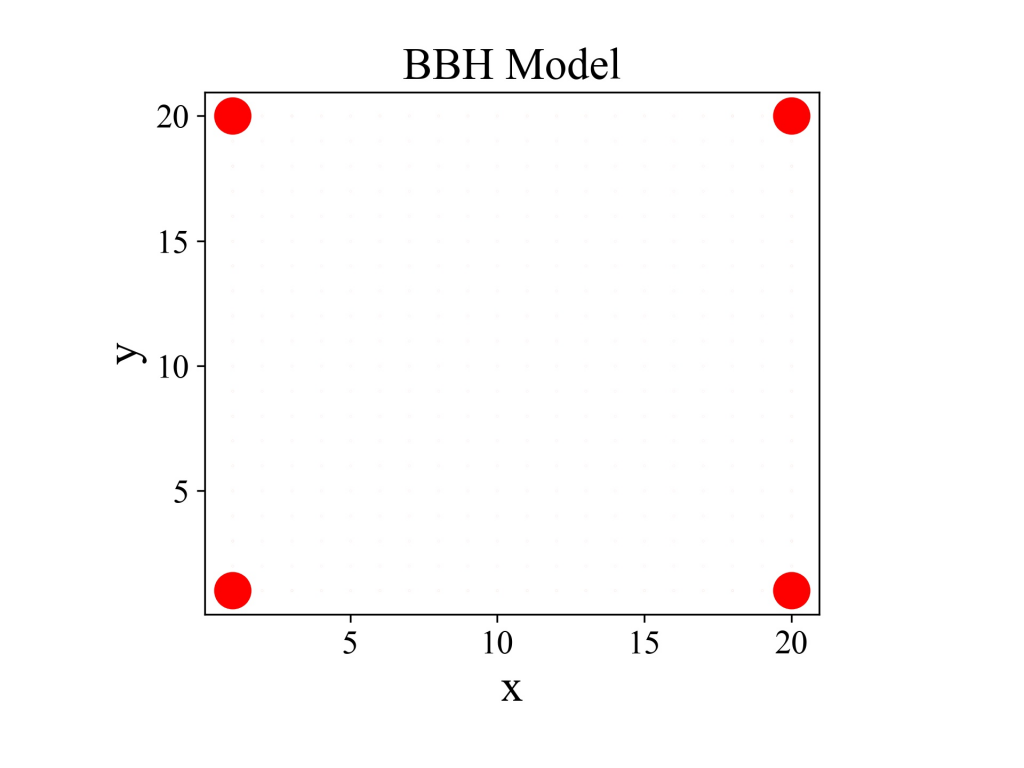
换一种画图方式(Plot 3D Surface):
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/8557
"""
import numpy as np
from math import *
def hamiltonian(Nx, Ny):
delta = 1e-3
gamma = 1e-3
lambda0 = 1
h = np.zeros((4*Nx*Ny, 4*Nx*Ny))
# 元胞内部跃迁
for x in range(Nx):
for y in range(Ny):
h[x*Ny*4+y*4+0, x*Ny*4+y*4+0] = delta
h[x*Ny*4+y*4+1, x*Ny*4+y*4+1] = delta
h[x*Ny*4+y*4+2, x*Ny*4+y*4+2] = -delta
h[x*Ny*4+y*4+3, x*Ny*4+y*4+3] = -delta
h[x*Ny*4+y*4+0, x*Ny*4+y*4+2] = gamma
h[x*Ny*4+y*4+0, x*Ny*4+y*4+3] = gamma
h[x*Ny*4+y*4+1, x*Ny*4+y*4+2] = -gamma
h[x*Ny*4+y*4+1, x*Ny*4+y*4+3] = gamma
h[x*Ny*4+y*4+2, x*Ny*4+y*4+0] = gamma
h[x*Ny*4+y*4+2, x*Ny*4+y*4+1] = -gamma
h[x*Ny*4+y*4+3, x*Ny*4+y*4+0] = gamma
h[x*Ny*4+y*4+3, x*Ny*4+y*4+1] = gamma
# y方向上的元胞间跃迁
for x in range(Nx):
for y in range(Ny-1):
h[x*Ny*4+y*4+0, x*Ny*4+(y+1)*4+3] = lambda0
h[x*Ny*4+(y+1)*4+1, x*Ny*4+y*4+2] = -lambda0
h[x*Ny*4+y*4+2, x*Ny*4+(y+1)*4+1] = -lambda0
h[x*Ny*4+(y+1)*4+3, x*Ny*4+y*4+0] = lambda0
# x方向上的元胞间跃迁
for x in range(Nx-1):
for y in range(Ny):
h[x*Ny*4+y*4+0, (x+1)*Ny*4+y*4+2] = lambda0
h[(x+1)*Ny*4+y*4+1, x*Ny*4+y*4+3] = lambda0
h[(x+1)*Ny*4+y*4+2, x*Ny*4+y*4+0] = lambda0
h[x*Ny*4+y*4+3, (x+1)*Ny*4+y*4+1] = lambda0
return h
def main():
Nx = 10
Ny = 10
fermi_energy = 0
h = hamiltonian(Nx, Ny)
green = np.linalg.inv((fermi_energy+1e-6j)*np.eye(h.shape[0])-h)
DOS = np.zeros((Ny*2, Nx*2))
for x in range(Nx):
for y in range(Ny):
DOS[y*2+1, x*2+1] = -np.imag(green[x*Ny*4+y*4+0, x*Ny*4+y*4+0])/pi
DOS[y*2+0, x*2+0] = -np.imag(green[x*Ny*4+y*4+1, x*Ny*4+y*4+1])/pi
DOS[y*2+1, x*2+0] = -np.imag(green[x*Ny*4+y*4+2, x*Ny*4+y*4+2])/pi
DOS[y*2+0, x*2+1] = -np.imag(green[x*Ny*4+y*4+3, x*Ny*4+y*4+3])/pi
DOS = DOS/np.sum(DOS)
Plot_3D_Surface(np.arange(1, 2*Nx+0.001), np.arange(1, 2*Ny+0.001), DOS, xlabel='x', ylabel='y', zlabel='DOS', title='BBH Model', filename='BBH Model')
def Plot_3D_Surface(x, y, matrix, xlabel='x', ylabel='y', zlabel='z', title='title', filename='a'):
import matplotlib.pyplot as plt
from matplotlib import cm
from matplotlib.ticker import LinearLocator
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
plt.subplots_adjust(bottom=0.1, right=0.65)
x, y = np.meshgrid(x, y)
if len(matrix.shape) == 2:
surf = ax.plot_surface(x, y, matrix, cmap=cm.coolwarm, linewidth=0, antialiased=False)
elif len(matrix.shape) == 3:
for i0 in range(matrix.shape[2]):
surf = ax.plot_surface(x, y, matrix[:,:,i0], cmap=cm.coolwarm, linewidth=0, antialiased=False)
ax.set_title(title, fontsize=20, fontfamily='Times New Roman')
ax.set_xlabel(xlabel, fontsize=20, fontfamily='Times New Roman')
ax.set_ylabel(ylabel, fontsize=20, fontfamily='Times New Roman')
ax.set_zlabel(zlabel, fontsize=20, fontfamily='Times New Roman')
# ax.set_zlim(-1, 1) # 设置z轴的范围
ax.zaxis.set_major_locator(LinearLocator(2)) # 设置z轴主刻度的个数
ax.zaxis.set_major_formatter('{x:.2f}') # 设置z轴主刻度的格式
ax.tick_params(labelsize=15) # 设置刻度值字体大小
labels = ax.get_xticklabels() + ax.get_yticklabels() + ax.get_zticklabels()
[label.set_fontname('Times New Roman') for label in labels] # 设置刻度值字体
cax = plt.axes([0.80, 0.15, 0.05, 0.75]) # color bar的位置 [左,下,宽度, 高度]
cbar = fig.colorbar(surf, cax=cax) # color bar
cbar.ax.tick_params(labelsize=15) # 设置color bar刻度的字体大小
for l in cbar.ax.yaxis.get_ticklabels():
l.set_family('Times New Roman')
# plt.savefig(filename+'.jpg', dpi=300)
plt.show()
plt.close('all')
if __name__ == '__main__':
main()计算结果为:
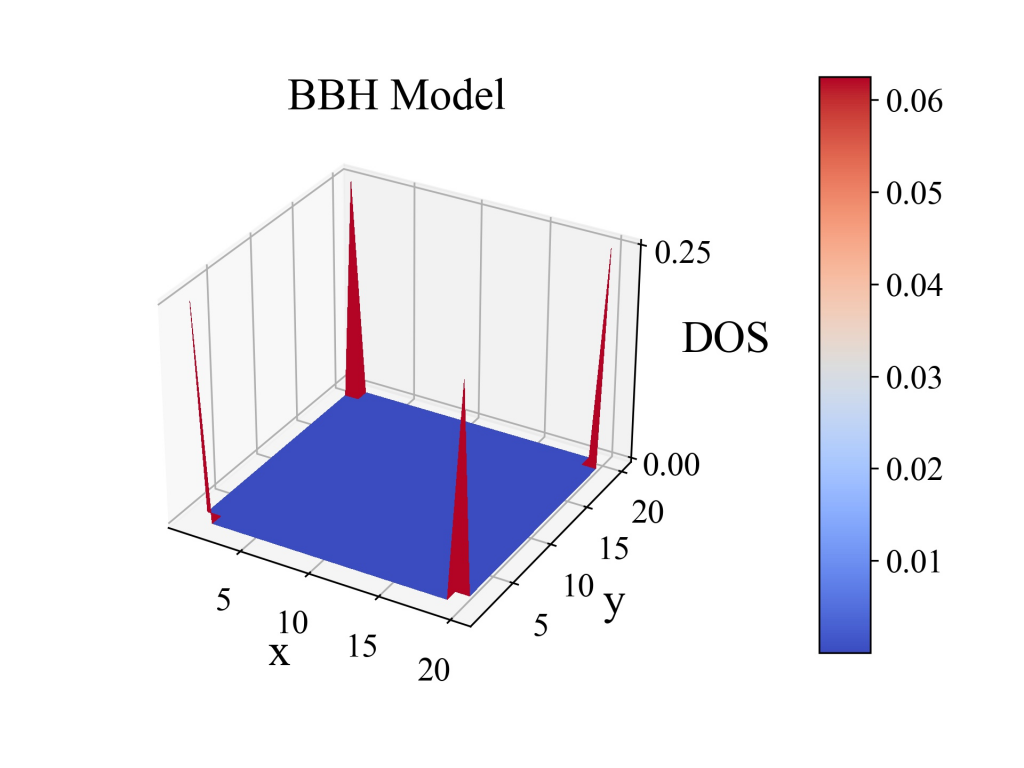
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】
请问你这个哈密顿量的代码是开边界的吧?在实空间这y方向周期边界怎么加?
是的。如果要在y方向上加周期性边界条件,那么需要对y=0和y=Ny之间加上跃迁项。
老师您好,如果这里的晶格是三角晶格,每个原胞都是菱形,里面有4个原子,那还能用这种方法开边界吗?比如像这样写 h[x*Ny*4+y*4+0, x*Ny*4+y*4+0] = delta
赋值看怎么编号了,都是可以的。对于需要开边界的地方,不要给相应的周期跃迁项。
要看体系自旋是半整数还是整数以及体系轨道的情况。一般来说N重转动算符的N次方正比于单位算符:如果是半整数自旋体系,那就等于负的单位算符。如果是整数自旋则为正的单位算符。
哦哦
DOS[y*2+1, x*2+1] = -np.imag(green[x*Ny*4+y*4+0, x*Ny*4+y*4+0])/pi
DOS[y*2+0, x*2+0] = -np.imag(green[x*Ny*4+y*4+1, x*Ny*4+y*4+1])/pi
等式左边方括号里的顺序可以换吗?比如换成这样:
DOS[y*2+0, x*2+0] = -np.imag(green[x*Ny*4+y*4+0, x*Ny*4+y*4+0])/pi
DOS[y*2+1, x*2+1] = -np.imag(green[x*Ny*4+y*4+1, x*Ny*4+y*4+1])/pi
这个顺序是怎么决定的呀?
都是可以的,看你怎么储存数据了。另外,不同编号顺序对物理结果没影响,但在整个计算过程中,编号需要采用同一个标准。
请问为什么胞内跃迁就是直接写γ,而胞间跃迁就是λ*exp(i*kx)?胞内跃迁不用考虑e指数项吗?只有考虑高阶拓扑相才这么操作吗?
参考这篇:以SSH模型为例子说明两种傅里叶变换方法。
大佬,您好,我看相关的高阶拓扑绝缘体的文章,里面会提到C2, C4, C6对称.这里主要指的是什么对称
旋转对称性,180度,90度,60度。
例如C4,意思是将晶格原胞旋转90度,体系跃迁矩阵保持不变?
旋转90度后和原先的重合。
那这篇BBH模型满足C4对称么?
不呀,除非x跃迁和y跃迁完全相同。参考:https://doi.org/10.1103/PhysRevB.96.245115 的 Eq (6.36).
博主,我想请教一下,C2, C4, C6 symmtry对应的算符和算符操作是什么?
不同角度的旋转对称性,也是循环群,参考:https://en.wikipedia.org/wiki/Cyclic_group。算符形式好像不唯一。
博主:
你算过高阶拓扑的边界极化么?
边界极化的量子化对应的就是高阶拓扑不变量,参考这篇:BBH模型的nested Wilson loop高阶不变量(附Python代码)。
请问作者,您知道BBH模型中的电荷密度图如何计算么?
我没算过。得根据定义来算,好像跟态密度的定义不会差太多
是不是通过热力学量平均值定义从而和Green function联系上的那种?如Abrikosov的P96,(10.25)
我也不是很了解,我猜电荷密度可能是需要对态密度进行能量上的积分。如果考虑有限温度,也是要考虑热力学平均。可以查查教材或文献,看有没有这个概念的定义。
这个局部态密度LDOS的物理含义是什么呀?
看程序里面是对(λ*I-H)求逆矩阵,然后将逆矩阵的每个元素按照原子排列分配给2*Nx*2*Ny个原子,最后对这些原子绘图
之前看到有个对二维弹性板(固体声学)做逆向设计的文章,也提到了LDOS,在那篇文章里面是把归一化后每个点的面外位移的平方定义为了LDOS
那么是不是弹性力学里面的结构矩阵也能定义成这个形式?
LDOS=local density of states,表示的是态密度在实空间的分布。波函数模的平方也能体现出电子在空间上的分布情况,归一化后是等价的,参考数值验证“波函数模平方分布”和“格林函数计算出的态密度分布”的关系(附Python代码)。
你说的弹性力学中的LDOS我不是很了解,估计也类似于波函数模的平方吧。是否能写出这种形式需要具体考虑或推导,或者查阅相关的文献。
非常感谢!
冒昧打扰一下楼主,想请问一下高阶拓扑相是怎么定义的?您可否一下定义高阶的文章?
有挺多文章和综述文献的,可以网上搜下。
楼主,您好!我有一个一直困扰的问题没有解决,想请教一下您:
在算矩阵本征值时,有时候python的结果误差比较大(和Fortran比较),得到的结果是不准确的。初步判断应该是精度不够的问题。想请问您,这该如何解决?
本征值应该都是一样的才对。看在python中矩阵是否定义为复数,例如np.zeros((x,y), dtype='complex')。
在内容一样的情况下,检查是很容易的。在某个语句前后分别输出结果,一步步对比验证。
冒昧打扰一下楼主,请问如果把四极矩的晶格形状正方形变成正六边形,那么角态会还集中在六个角吗,哈密顿量该怎么改写呢?
对称性不一样,具体的形式和结果我也不确定。可能有这方面的文献吧,可以找一找看。
哦好的,谢谢您,我有查到了相关的论文,“Higher-Order Topological Insulator in Twisted Bilayer Graphene”,讲述了石墨烯晶格中的情况,角态和这个类似。
还想再请问您,这个BBH模型中它后面讲述的八极矩的程序该怎么在您的四极矩的基础上改进,我看您第二段程序是换了一种画图方式,内容还是四极矩的。
实空间的哈密顿量需要重新写。八级矩一般是要画三维的分布图,可以参考:使用matplotlib画图。计算输出的数据格式不唯一,根据画图程序的要求调整。