之前写过一些哈密顿量矩阵的赋值代码,可能不是特别直观。这里给出哈密顿量矩阵的具体的形式。
以3×3点方格子为例。示意图如下:
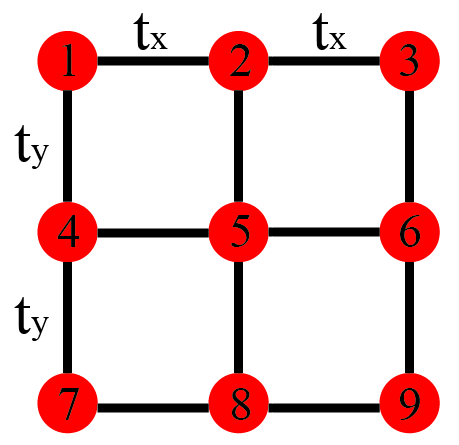
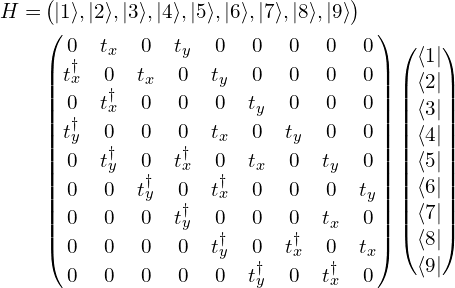
Python实现代码:
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/5375
"""
import numpy as np
def hamiltonian(width=3, length=3): # 方格子哈密顿量
h = np.zeros((width*length, width*length))
# y方向的跃迁
for x in range(length):
for y in range(width-1):
h[x*width+y, x*width+y+1] = 1
h[x*width+y+1, x*width+y] = 1
# x方向的跃迁
for x in range(length-1):
for y in range(width):
h[x*width+y, (x+1)*width+y] = 1
h[(x+1)*width+y, x*width+y] = 1
return h
h = hamiltonian()
print(h)运行结果为:
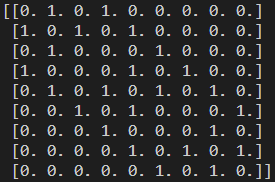
此外,以上哈密顿量可以写为更紧凑的形式:
![]()
可以进一步改写成张量积形式[1]:
![]()
张量积形式的代码为:
"""
This code is supported by the website: https://www.guanjihuan.com
The newest version of this code is on the web page: https://www.guanjihuan.com/archives/5375
"""
import numpy as np
def hamiltonian(width=3, length=3): # 方格子哈密顿量
hopping_x = np.zeros((length, length))
hopping_y = np.zeros((width, width))
for i in range(length-1):
hopping_x[i, i+1] = 1
hopping_x[i+1, i] = 1
for i in range(width-1):
hopping_y[i, i+1] = 1
hopping_y[i+1, i] = 1
h = np.kron(hopping_x, np.eye(width))+np.kron(np.eye(length), hopping_y)
return h
h = hamiltonian()
print(h)运算结果和上面代码的结果相同。
参考资料:
[1] 二维方格Hofstadter's butterfly
【说明:本站主要是个人的一些笔记和代码分享,内容可能会不定期修改。为了使全网显示的始终是最新版本,这里的文章未经同意请勿转载。引用请注明出处:https://www.guanjihuan.com】
关老师,如果是三维立方晶格的哈密顿量该如何描述?
做好编号在对应的元素上赋值就可以了,或者用张量积的形式,再加上一个张量积。
博主 你的张量积哈密顿量是有问题的,你可以做符号运算,把tx ty带进去,可以发现结果和示意图下那个有tx ty的矩阵不一样,刚好tx ty反了
我把tx和ty换成不同的值,验算的结果是对的上的,好像没问题。
如果对不上,把张量积的顺序对调一下就可以了,或者前面的编号重新编写,把y方向的先编号。
也可以不用管,虽然矩阵形式是不一样了,但物理量结果是一样的,影响不大。
请问您假设的边条件是什么?要是周期边条件呢?
这里是开放边界条件。周期边界条件也是可以考虑,在上下、左右连接的地方加上跃迁项。
“在上下、左右连接的地方加上跃迁”,这个还能说的再详细一下吗?谢谢!
在有连线的地方加上跃迁。例如1和4相连接,所以相应的矩阵元位置需要赋值。
请问这里的哈密顿量对角化后会有9个特征值和特征向量,如何分辨每个特征值是哪个格点的能量呢,特征值的排序好像是随机的,并没有和原来的原子顺序对应上
特征值(本征值)是整个体系的能量,没有和位置对应的。波函数的分量可以和位置对应,模的平方是概率分布。
嗯嗯,波函数和位置可以对应,特征向量就是波函数,特征向量和特征值是一一对应的,特征值随机排序了,特征向量也随机排序了,那该如何确定哪个特征向量对应哪个格点位置呢,,
我用软件对角化的的时候,给出的特征向量排序是随机的,分不清哪一列对应原来的格点顺序
我刚刚发现特征值随机排序,但是特征向量排序是不会改变的,多谢大哥!
还是不对,我用matlab和python分别对角化同一个矩阵,给出的特征值和特征向量虽然一一对应,但是排序不一样
是某个波函数的分量和格点是一一对应的,不是波函数。本征值本身没有和格点的一一对应关系。
有的求本征值算法是排序的,比如从小到大,有的没有,但没什么影响。
嗯嗯,多谢解答
请问大神可以找一下斜对角,次近邻填矩阵元的规律吗
在实空间填矩阵元,是需要慢慢找规律。可以从简单的例子出发,对每个项赋值,然后再推广到任意大小。如果有周期性边界条件时,还得再多考虑一种情况,单独写个代码赋值。而关于斜对角和次近邻的傅里叶变换,可以参考这篇后面的内容:离散格子的傅里叶变换和反傅里叶变换。
用python的vectorization的方法写可能会更简洁优雅
vectorization的意思是直接就写成数组的样子吗?我这里循环赋值可以方便推广到不同大小的体系。
厉害!!!
谢谢